Free PDF Download of CBSE Class 10 Maths Chapter 4 Quadratic Equations Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Quadratic Equations MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 4 Quadratic Equations
1. Which of the following is not a quadratic equation
(a) x² + 3x – 5 = 0
(b) x² + x3 + 2 = 0
(c) 3 + x + x² = 0
(d) x² – 9 = 0
Answer/Explanation
Answer: b
Explaination:Reason: Since it has degree 3.
2. The quadratic equation has degree
(a) 0
(b) 1
(c) 2
(d) 3
Answer/Explanation
Answer: c
Explaination:Reason: A quadratic equation has degree 2.
3. The cubic equation has degree
(a) 1
(b) 2
(c) 3
(d) 4
Answer/Explanation
Answer: c
Explaination:Reason: A cubic equation has degree 3.
4. A bi-quadratic equation has degree
(a) 1
(b) 2
(c) 3
(d) 4
Answer/Explanation
Answer: d
Explaination:Reason: A bi-quadratic equation has degree 4.
5. The polynomial equation x (x + 1) + 8 = (x + 2) {x – 2) is
(a) linear equation
(b) quadratic equation
(c) cubic equation
(d) bi-quadratic equation
Answer/Explanation
Answer: a
Explaination:Reason: We have x(x + 1) + 8 = (x + 2) (x – 2)
⇒ x² + x + 8 = x² – 4
⇒ x² + x + 8- x² + 4 = 0
⇒ x + 12 = 0, which is a linear equation.
6. The equation (x – 2)² + 1 = 2x – 3 is a
(a) linear equation
(b) quadratic equation
(c) cubic equation
(d) bi-quadratic equation
Answer/Explanation
Answer: b
Explaination:Reason: We have (x – 2)² + 1 = 2x – 3
⇒ x² + 4 – 2 × x × 2 + 1 = 2x – 3
⇒ x² – 4x + 5 – 2x + 3 = 0
∴ x² – 6x + 8 = 0, which is a quadratic equation.
7. The roots of the quadratic equation 6x² – x – 2 = 0 are

Answer/Explanation
Answer: c
Explaination:Reason: We have 6×2 – x – 2 = 0
⇒ 6x² + 3x-4x-2 = 0
⇒ 3x(2x + 1) -2(2x + 1) = 0
⇒ (2x + 1) (3x – 2) = 0
⇒ 2x + 1 = 0 or 3x – 2 = 0
∴ x =\(-\frac{1}{2}\), x = \(\frac{2}{3}\)
8. The quadratic equation whose roots are 1 and
(a) 2x² + x – 1 = 0
(b) 2x² – x – 1 = 0
(c) 2x² + x + 1 = 0
(d) 2x² – x + 1 = 0
Answer/Explanation
Answer: b
Explaination:Reason: Required quadratic equation is
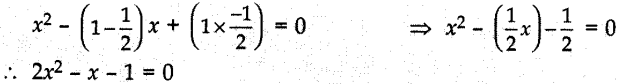
9. The quadratic equation whose one rational root is 3 + √2 is
(a) x² – 7x + 5 = 0
(b) x² + 7x + 6 = 0
(c) x² – 7x + 6 = 0
(d) x² – 6x + 7 = 0
Answer/Explanation
Answer: d
Explaination:Reason: ∵ one root is 3 + √2
∴ other root is 3 – √2
∴ Sum of roots = 3 + √2 + 3 – √2 = 6
Product of roots = (3 + √2)(3 – √2) = (3)² – (√2)² = 9 – 2 = 7
∴ Required quadratic equation is x² – 6x + 7 = 0
10. The equation 2x² + kx + 3 = 0 has two equal roots, then the value of k is
(a) ±√6
(b) ± 4
(c) ±3√2
(d) ±2√6
Answer/Explanation
Answer: d
Explaination:Reason: Here a = 2, b = k, c = 3
Since the equation has two equal roots
∴ b² – 4AC = 0
⇒ (k)² – 4 × 2 × 3 = 0
⇒ k² = 24
⇒ k = ± √24
∴ k= ± \(\pm \sqrt{4 \times 6}\) = ± 2√6
11. The roots of the quadratic equation \(x+\frac{1}{x}=3\), x ≠ 0 are.
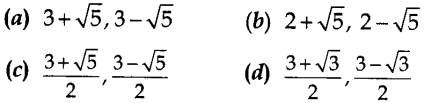
Answer/Explanation
Answer: c
Explaination:Reason: We have \(x+\frac{1}{x}=3\)
⇒ \(\frac{x^{2}+1}{x}=3\)
⇒ x² + 1 = 3x
On comparing with ax² + bx + c = 0
∴ a = 1, b = – 3, c = 1
⇒ D = b² – 4ac = (-3)² – 4 × (1) × (1) = 9 – 4 = 5
12. The roots of the quadratic equation 2x² – 2√2x + 1 = 0 are

Answer/Explanation
Answer: c
Explaination:Reason: Here a = 2, b = -2√2 , c = 1
∴ D = b² – 4ac = (-2√2 )² – 4 × 2 × 1 = 8 – 8 = 0
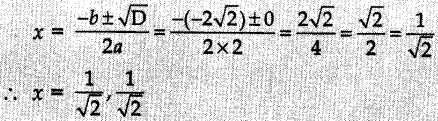
13. The sum of the roots of the quadratic equation 3×2 – 9x + 5 = 0 is
(a) 3
(b) 6
(c) -3
(d) 2
Answer/Explanation
Answer: c
Explaination:Reason: Here a = 3, b = -9, c = 5
∴ Sum of the roots \(=\frac{-b}{a}=-\frac{(-9)}{3}=3\)
14. If the roots of ax2 + bx + c = 0 are in the ratio m : n, then
(a) mna² = (m + n) c²
(b) mnb² = (m + n) ac
(c) mn b² = (m + n)² ac
(d) mnb² = (m – n)² ac
Answer/Explanation
Answer: c
Explaination:

15. If one root of the equation x² + px + 12 = 0 is 4, while the equation x² + px + q = 0 has equal roots, the value of q is

Answer/Explanation
Answer: a
Explaination:Reason: Since 4 is a root of x² + px + 12 = 0
∴ (4)² + p(4) + 12 = 0
⇒ p = -7
Also the roots of x² + px + q = 0 are equal, we have p² – 4 x 1 x q = 0
⇒ (-7)² -4q = 0
\(\therefore q=\frac{49}{4}\)
16. a and p are the roots of 4x² + 3x + 7 = 0, then the value of \(\frac{1}{\alpha}+\frac{1}{\beta}\) is

Answer/Explanation
Answer: b
Explaination:
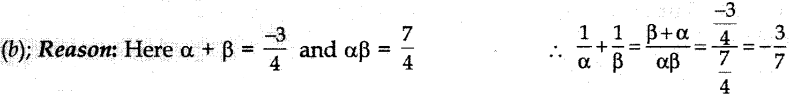
17. If a, p are the roots of the equation (x – a) (x – b) + c = 0, then the roots of the equation (x – a) (x – P) = c are
(a) a, b
(b) a, c
(c) b, c
(d) none of these
Answer/Explanation
Answer: a
Explaination:Reason: By given condition, (x – a) (x – b) + c = (x – α) (x – β)
⇒ (x – α) (x – β) – c = (x – a) (x – b)
This shows that roots of (x – α) (x – β) – c are a and b
18. Mohan and Sohan solve an equation. In solving Mohan commits a mistake in constant term and finds the roots 8 and 2. Sohan commits a mistake in the coefficient of x. The correct roots are
(a) 9,1
(b) -9,1
(c) 9, -1
(d) -9, -1
Answer/Explanation
Answer: a
Explaination:Reason: Correct sum = 8 + 2 = 10 from Mohan
Correct product = -9 x -1 = 9 from Sohan
∴ x² – (10)x + 9 = 0
⇒ x² – 10x + 9 = 0
⇒ x² – 9x – x + 9
⇒ x(x – 9) – 1(x – 9) = 0
⇒ (x-9) (x-l) = 0 .
⇒ Correct roots are 9 and 1.
19. If a and p are the roots of the equation 2x² – 3x – 6 = 0. The equation whose roots are \(\frac{1}{\alpha}\) and \(\frac{1}{\beta}\) is
(a) 6x² – 3x + 2 = 0
(b) 6x² + 3x – 2 = 0
(c) 6x² – 3x – 2 = 0
(d) x² + 3x-2 = 0
Answer/Explanation
Answer: b
Explaination:
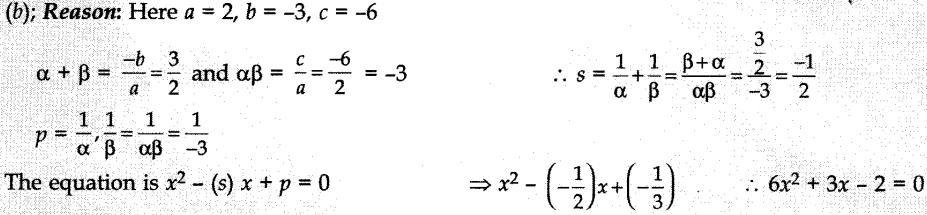
20. If the roots of px2 + qx + 2 = 0 are reciprocal of each other, then
(a) P = 0
(b) p = -2
(c) p = ±2
(d) p = 2
Answer/Explanation
Answer: d
Explaination:Reason: here α = \(\frac{1}{β}\)
∴ αβ = 1
⇒ \(\frac{2}{p}\) = 1
∴ p = 2
21. If one root of the quadratic equation 2x² + kx – 6 = 0 is 2, the value of k is
(a) 1
(b) -1
(c) 2
(d) -2
Answer/Explanation
Answer: b
Explaination:Reason: Scice x = 2 is a root of the equation 2x² + kx -6 = 0
∴ 2(2)² +k(2) – 6 = 0
⇒ 8 + 2k – 6 = 0
⇒ 2k = -2
∴ k = -1
22. The roots of the quadratic equation
![]()
(a) a, b
(b) -a, b
(c) a, -b
(d) -a, -b
Answer/Explanation
Answer: d
Explaination:
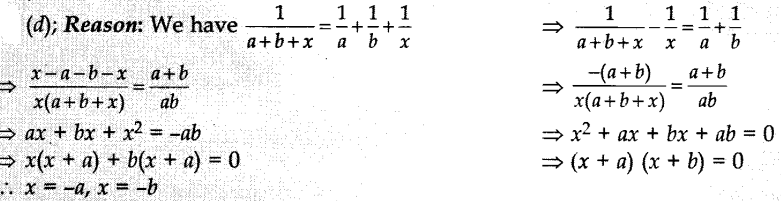
23. The roots of the equation 7x² + x – 1 = 0 are
(a) real and distinct
(b) real and equal
(c) not real
(d) none of these
Answer/Explanation
Answer: a
Explaination:Reason: Here a = 2, b = 1, c = -1
∴ D = b² – 4ac = (1)² – 4 × 2 × (-1) = 1 + 8 = 9 > 0
∴ Roots of the given equation are real and distinct.
24. The equation 12x² + 4kx + 3 = 0 has real and equal roots, if
(a) k = ±3
(b) k = ±9
(c) k = 4
(d) k = ±2
Answer/Explanation
Answer: a
Explaination:Reason: Here a = 12, b = 4k, c = 3
Since the given equation has real and equal roots
∴ b² – 4ac = 0
⇒ (4k)² – 4 × 12 × 3 = 0
⇒ 16k² – 144 = 0
⇒ k² = 9
⇒ k = ±3
25. If -5 is a root of the quadratic equation 2x² + px – 15 = 0, then
(a) p = 3
(b) p = 5
(c) p = 7
(d) p = 1
Answer/Explanation
Answer: c
Explaination:Reason: Since – 5 is a root of the equation 2x² + px -15 = 0
∴ 2(-5)² + p (-5) – 15 = 0
⇒ 50 – 5p -15 = 0
⇒ 5p = 35
⇒ p = 7
26. If the roots of the equations ax² + 2bx + c = 0 and bx² – 2√ac x + b = 0 are simultaneously real, then
(a) b = ac
(b) b2 = ac
(c) a2 = be
(d) c2 = ab
Answer/Explanation
Answer: b
Explaination:Reason: Given equations have real roots, then
D1 ≥ 0 and D2 ≥ 0
(2b)² – 4ac > 0 and (-2√ac)² – 4b.b ≥ 0
4b² – 4ac ≥ 0 and 4ac – 4b2 > 0
b² ≥ ac and ac ≥ b²
⇒ b² = ac
27. The roots of the equation (b – c) x² + (c – a) x + (a – b) = 0 are equal, then
(a) 2a = b + c
(b) 2c = a + b
(c) b = a + c
(d) 2b = a + c
Answer/Explanation
Answer: d
Explaination:Reason: Since roots are equal
∴ D = 0 => b² – 4ac = 0
⇒ (c – a)² -4(b – c) (a – b) = 0
⇒ c² – b² – 2ac -4(ab -b² + bc) = 0 =>c + a-2b = 0 => c + a = 2b
⇒ c² + a² – 2ca – 4ab + 4b² + 4ac – 4bc = 0
⇒ c² + a² + 4b² + 2ca – 4ab – 4bc = 0
⇒ (c + a – 2b)² = 0
⇒ c + a – 2b = 0
⇒ c + a = 2b
28. A chess board contains 64 equal squares and the area of each square is 6.25 cm². A border round the board is 2 cm wide. The length of the side of the chess board is
(a) 8 cm
(b) 12 cm
(c) 24 cm
(d) 36 cm
Answer
Answer: c
29. One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son’s age. Their present ages are
(a) 7 years, 49 years
(b) 5 years, 25 years
(c) 1 years, 50 years
(d) 6 years, 49 years
Answer
Answer: a
30. The sum of the squares of two consecutive natural numbers is 313. The numbers are
(a) 12, 13
(b) 13,14
(c) 11,12
(d) 14,15
Answer
Answer: a
31. Which of the following is not a quadratic equation? [NCERT Exemplar Problems]
(a) 2(x – 1)² = 4x² – 2x + 1
(b) 2x – x² = x² + 5
(c) (√2x + √3 )² + x² = 3x² – 5x
(d) (x² + 2x)² = x4 + 3 + 4x3
Answer/Explanation
Answer: c
Explaination:
2x² + 3 + 2√6 x + x² = 3x² – 5x
2√6x + 5x + 3 = 0
32. If (x – a) is one of the factors of the polynomial ax² + bx + c, then one of the roots of ax² + bx + c = 0 is
(a) 1
(b) c
(c) a
(d) none of these
Answer/Explanation
Answer: c
Explaination:
∵ x – a is one of the factors one root = a.
33. Which of the following are the roots of the quadratic equation, x² – 9x + 20 = 0 by factorisation?
(a) 3, 4
(b) 4, 5
(c) 5, 6
(d) 6, 1
Answer/Explanation
Answer: b
Explaination:
Given equation is x² – 9x + 20 = 0
⇒ x² – 5x – 4x + 20 = 0
⇒ x(x – 5) – 4(x – 5) = 0
⇒ (x – 5) (x – 4) = 0
⇒ either x – 5 = 0 and x – 4 = 0
⇒ x = 5 and x = 4
∴ x = 4 and 5 are the roots/solution of the given quadratic equation.
34. If (1 – p) is a root of the equation x² + px + 1 -p = 0, then roots are
(a) 0, 1
(b) -1, 1
(c) 0, -1
(d) – 1, 2
Answer/Explanation
Answer: c
Explaination:
(1 -p) is a root
∴ (1 – p)² + p(1 – p)+ 1 – p = 0
⇒ (1 – p)[1 – p + p + 1] = 0
⇒ (1 – p)(2) = 0
⇒ p=1
x²+x = 0
One root = 0 and another root = – 1
∴ roots are 0 and – 1.
35. If a, P are roots of the equation x² + 5x + 5 = 0, then equation whose roots are a + 1 and p + 1 is
(a) x² + 5x – 5 = 0
(b) x² + 3x + 5 = 0
(c) x² + 3x + 1 = 0
(d) none of these
Answer/Explanation
Answer: c
Explaination:
α + β = -5, αβ = 5.
Required equation is x² – (α + 1 + β + 1)x + (α + 1) (β + 1) = 0
⇒ x² – (α + β + 2)x + (αβ + α + β +1) = 0
⇒ x² – (-5 + 2)x + (5 – 5 + 1) = 0
⇒ x² + 3x + 1 = 0
36. Which of the following equations has two distinct real roots? [NCERT Exemplar Problems]
(a) 2x² – 3√2x + \(\frac{9}{4}\) =0
(b) x² + x – 5 = 0
(c) x² + 3x + 2√2 = 0
(d) 5x² – 3x + 1 = 0
Answer/Explanation
Answer: b
Explaination: (b) D > 0
37. Which of the following equations has no real roots ? [NCERT Exemplar Problems]
(a) x² – 4x + 3√2 =0
(b) x² + 4x – 3√2 = 0
(c) x² – 4x – 3√2 = 0
(d) 3x² + 4√3x + 4 = 0
Answer/Explanation
Answer: a
Explaination: (a) D < 0
38. (x² + 1)² – x² = 0 has [NCERT Exemplar Problems]
(a) four real roots
(b) two real roots
(c) no real roots
(d) one real root
Answer/Explanation
Answer: c
Explaination: (c) no real roots
39. If the difference of the roots of the equation x² – bx + c = 0 be 1, then
(a) b² – 4c + 1 = 0
(b) b² + 4c = 0
(c) b² – 4c – 1 – 0
(d) b² – 4c = 0
Answer/Explanation
Answer: c
Explaination:
Let roots are α and β
⇒ α – β = 1
∵ (α – β)² = (α + β)² – 4αβ
⇒ 1 = b² – 4c
⇒ b² – 4c – 1 = 0
40. If α + β = 4 and α3 + β3 = 44, then a, p are the roots of the equation
(a) 2x² – 7x – 7 = 0
(b) 3x² + 8x + 12 = 0
(c) 3x² – 12x + 5 = 0
(d) none of these
Answer/Explanation
Answer: d
Explaination:
α3 + β3 = (α + β)3 – 3αβ(α + β)
⇒ 44 = (4)3 – 3αβ × 4
⇒ 44 – 64 = – 12 αβ
⇒ αβ \(=\frac{20}{12}=\frac{5}{3}\)
∴ quadratic equation is
x² – (α + β)x + αβ = 0
⇒ x² – 4x + \(\frac{5}{3}\) = 0
⇒ 3x² – 12x + 5 = 0
41. If the roots of equation 3x² + 2x + (p + 2)(p – 1) = 0 are of opposite sign then which of the following cannot be the value of p?
(a) 0
(b) – 1
(c) \(\frac{1}{2}\)
(d) – 3
Answer/Explanation
Answer: d
Explaination:
∵ roots are of opposite sign
∴ product of the roots is negative
⇒ (p + 2)(p – 1) should be negative.
Clearly when p = – 3, (p + 2) (p – 1) is not negative.
42. The value of k for which the equation x² + 2(k + 1)x + k² = 0 has equal roots is
(a) – 1
(b) –\(\frac{1}{2}\)
(c) 1
(d) none of these
Answer/Explanation
Answer: b
Explaination:
For equal roots, D = 0
⇒ [2(k+ 1)]² – 4 × k²=0
⇒ 4(k + 1)² – 4k² =0
⇒ 4(k² + 2k + 1) – 4k² = 0
⇒ 8k + 4 = 0
⇒ k = \(\frac{-1}{2}\)
43. If the equation x² – (2 + m)x + (-m² – 4m – 4) = 0 has coincident roots, then
(a) m = 0, m = 1
(b) m = 2, m = 2
(c) m = -2, m = -2
(d) m = 6, m = 1
Answer/Explanation
Answer: c
Explaination:
For coincident roots, D = 0
⇒ [-(2 + m)]² – 4 × 1 × (- m² – 4m – 4) = 0
⇒ (2 + m)² + 4(m² + 4m + 4) = 0
⇒ (2 + m)² + 4(m + 2)² = 0
⇒ 5(2 + m)² = 0
⇒ (2 + m)² = 0
⇒ m = -2.
44. If x = 2 is a solution of the equation x² – 5x + 6k = 0, the value of k is ______ .
Answer/Explanation
Answer:
Explaination:
Substituting x = 2, we have
(2)² – 5x² + 6k = 0
⇒ 4 – 10 + 6k = 0
⇒ k = 1
45. Check whether the following are quadratic equations:
(i) (x – 2) (x + 5) = (x – 3) (x + 4) + x²
(ii) x² – 3x + 5 = (x + 5)²
(iii) x3 – 3x² + 5x = (x – 2)3
(iv) (x – 7)x = 3X2 – 5
(v) (x² + 1) (x + 2) = (x + 3)²
(vi) (2x + 1) (x – 3) = (x – 1)²
Answer/Explanation
Answer:
Explaination:
(i) Given equation is (x – 2) (x + 5) = (x – 3)(x + 4) + x²
⇒ x² + 3x- 10 = x² + x- 12 + x²
⇒ x² – 2x – 2 = 0
which is of the form ax² + bx + c = 0
So, it is a quadratic equation.
(ii) Given equation is x² – 3x + 5 = (x + 5)²
⇒ x² – 3x + 5 = x² + 10x + 25
⇒ 13x + 20 = 0
which is not of the form ax² + bx+ c = 0
Hence, it is not a quadratic equation.
(iii) Here given equation is x3 – 3x² + 5x = (x – 2)3
⇒ x3 – 3x² + 5x = x3 – 6x² + 12x – 8
⇒ 3x² – 7x + 8 = 0
which is of the form ax² + bx + c = 0
Hence, given equation is a quadratic equation.
(iv) Given equation is (x – 7)x = 3x² – 5
⇒ x² – 7x = 3x² – 5
⇒ x² + 7x – 5 = 0
which of the form ax² + bx + c = 0
Hence, given equation is a quadratic equation.
(v) Given equation is
(x² + 1) (x + 2) = (x + 3)²
⇒ x3 + 2x² + x + 2 = x² + 6x + 9
⇒ x3 + x² – 5x – 7 = 0
It is of degree 3 and is not of the form ax² + bx + c = 0
Hence, given equation is not a quadratic equation.
(vi) (2x + 1) (x – 3) = (x – 1)²
⇒ 2x² – 6x + x – 3 = x² – 2x + 1
⇒ x² — 3x — 4 = 0
which is of the form ax2 + bx + c – 0
Hence, given equation is a quadratic equation.
46. Is x = -2 a solution of the equation x² – 2x + 8 = 0?
Answer/Explanation
Answer:
Explaination:
x² – 2x + 8 = 0
When x = – 2, LHS = (-2)² – 2(-2) + 8
= 4 + 4 + 8 = 16 ≠ 0
∴ x = – 2 is not a solution of the given equation.
47. If x = 3 is one root of the quadratic equation x² – 2kx -6 = 0, then find the value of k. [CBSE 2018]
Answer/Explanation
Answer:
Explaination:
Putting x = 3 in x² – 2kx – 6 = 0, we get
3² – 2k × 3 – 6 = 0
⇒ 9 – 6k – 6 = 0
⇒ 3 – 6k = 0
⇒ 3 = 6k
∴ k = \(\frac{3}{6}\) = \(\frac{1}{2}\)
48. Are x = 0, x = 1 the solution of the equation x² + x + 1 = 0?
Answer/Explanation
Answer:
Explaination:
Given equation is x² + x + 1 = 0
When x = 0, LHS = 0² + 0+ 1 = 1 ≠ 0
∴ x = 0 is not the solution.
When x = 1, LHS = 1² + 1 + 1= 3 ≠ 0
∴ x=1 is not the solution of given equation.
49. Ruchir was asked his age by his friend. Ruchir said “The number you get when you subtract 25 times my age from twice the square of my age will be thrice your age.. If the friend’s age is 14 years, then the age of Ruchir is_______ .
Answer/Explanation
Answer:
Explaination:
Let Ruchir’s age = x
A.T.Q. 2x² – 25x = 3 × 14
⇒ 2x² – 25x – 42 = 0
⇒ x = 14 years
50. The number of integral values of x so that 22x² – 7 + 5 = 1 is ______ .
Answer/Explanation
Answer:
Explaination:
22x² – 7x + 5 = 1
⇒ 2x² – 7x + 5 = 0
⇒ x = 1, \(\frac{5}{2}\)
∴ Integral value of x = 1.
51. Solve the following quadratic equation by factorisation: √3x² + 10x + 7√3 = 0.
Answer/Explanation
Answer:
Explaination:
√3x² + 10x + 7√3 = 0
⇒ √3 x² + 7x + 3x + 7√3 = 0
⇒ x (√3x + 7) + √3(√3x + 7) = 0
⇒ (√3x + 7)(x + √3) = 0
⇒ x = \(\frac{-7}{\sqrt{3}}\) or x = -√3
52. If p, q and r are rational numbers and p ≠ q ≠ r, then roots of the equation (p² – q²)x² – (q² – r²)x + (r² – p²) = 0 are
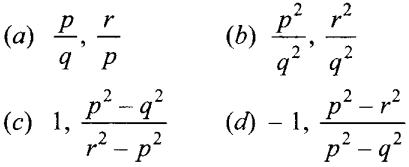
Answer/Explanation
Answer: d
Explaination:
Putting x = – 1, we have
(p² – q²)(-1)² – (q² – r²)(-1) + (r² – p²)
⇒ p² – q² + q² – r² + r² – p² = 0
∴ x = – 1 is one root. Only option (d) has one root – 1.
53. If α, β are roots of x² + 5x + a = 0 and 2α + 5β = -1, then a is equal to.
Answer/Explanation
Answer: d
Explaination:
Here α + β = -5 …(i)
and 2α + 5β = -1 …(ii)
Multiplying (i) by 2, we get
⇒ 2α + 2β = – 10 …(iii)
Solving (ii) and (iii), we get α = -8, β = 3
Now αβ = \(\frac{a}{1}\)
⇒ a = -24
54. α, β are roots of the equation (a + 1 )x² + (2a + 3)x + (3a + 4) = 0. If α . β = 2, then α + β =
Answer/Explanation
Answer:
Explaination:
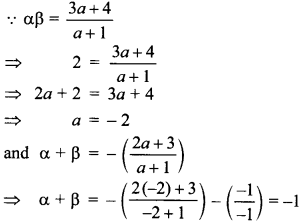
55. If the roots of the equation 12x² + mx + 5 = 0 are in the ratio 3 : 2, then m equals______ .
Answer/Explanation
Answer:
Explaination:
Let roots are 3x and 2x.
Sum of roots = 3x + 2x = 5x = \(\frac{-m}{12}\)
⇒ x = \(\frac{-m}{60}\) ……(i)
Product of roots = 3x.2x = 6x² = \(\frac{5}{12}\)
⇒ x² = \(\frac{5}{72}\) ……(ii)
From (i) and (ii), \(\frac{m²}{3600}\) = \(\frac{5}{12}\)
m² = 5 × 50
m² = 5 × 5 × 10
m = 5√10
56. For what value of k. the roots of the equation x² + 4x + k = 0 are real? [Delhi 2019]
Answer/Explanation
Answer:
Explaination:
D = b² – 4ac
⇒ D = (4)² – 4 × 1 × k
⇒ D = 16 – 4k
For real roots, D ≥ 0
⇒ 16 -4k ≥ 0
⇒ 16 ≥ 4k
⇒ k ≤ 4
57. Write the nature of roots of quadratic equation 4x² + 4√3x + 3 = 0.
Answer/Explanation
Answer:
Explaination:
Given equation is 4x² + 4√3x + 3 = 0,
Here a = 4, b = 4√3, c = 3
D = b² – Aac = 48 – 48 = 0
As D = 0, the equation has real and equal roots.
58. Write the nature of roots of quadratic equation : 4x² + 6x + 3 = 0
Answer/Explanation
Answer:
Explaination:
Given quadratic equation is 4c² + 6x + 3 = 0.
Here, a = 4, b = 6, c = 3
D = b² – 4ac
⇒ D = (6)² – 4 × 4 × 3
= 36 – 48 = -12 < 0
∴ Given quadratic equation has no real roots.
59. If arithmetic mean of two numbers a and b is 8 and ab = 9, find a quadratic equation whose roots are a and b.
Answer/Explanation
Answer:
Explaination:
Here \(\frac{a+b}{2}\)= 8
⇒ a + 6 = 16 and ab = 9
Now, quadratic equation whose roots are a and b is
x² – (a + b)x + ab = 0
⇒ x² – 16x + 9 = 0
60. If 2x² – (2 + k)x + k = 0 where k is a real number, find the roots of the equation.
Answer/Explanation
Answer:
Explaination:
Given quadratic equation is 2x² – (2 + k)x + k = 0.
Here, a = 2, b = -(2 + k), c = k
Now, a + b + c = 2 + [-(2 + k)] + k = 0
∴ roots are 1 and \(\frac{k}{2}\).
(If a + b + c = 0, then roots of the quadratic equation are 1 and \(\frac{c}{a}\))
We hope the given MCQ Questions for Class 10 Maths Quadratic Equations with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 4 Quadratic Equations Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.