Free PDF Download of CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Pair of Linear Equations in Two Variables MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 3 Pair of Linear Equations in Two Variables
1. A pair of linear equations a1x + b1y + c1 = 0; a2x + b2y + c2 = 0 is said to be inconsistent, if
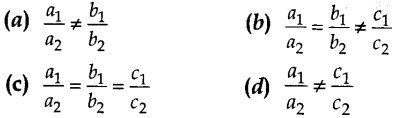
Answer
Answer: b
2. Graphically, the pair of equations 7x – y = 5; 21x – 3y = 10 represents two lines which are
(a) intersecting at one point
(b) parallel
(c) intersecting at two points
(d) coincident
Answer
Answer: b
3. The pair of equations 3x – 5y = 7 and – 6x + 10y = 7 have
(a) a unique solution
(b) infinitely many solutions
(c) no solution
(d) two solutions
Answer
Answer: c
4. If a pair of linear equations is consistent, then the lines will be
(a) always coincident
(b) parallel
(c) always intersecting
(d) intersecting or coincident
Answer
Answer: d
5. The pair of equations x = 0 and x = 5 has
(a) no solution
(b) unique/one solution
(c) two solutions
(d) infinitely many solutions
Answer
Answer: c
6. The pair of equation x = – 4 and y = – 5 graphically represents lines which are
(a) intersecting at (- 5, – 4)
(b) intersecting at (- 4, – 5)
(c) intersecting at (5, 4)
(d) intersecting at (4, 5)
Answer
Answer: b
7. For what value of k, do the equations 2x – 3y + 10 = 0 and 3x + ky + 15 = 0 represent coincident lines

Answer
Answer: a
8. If the lines given by 2x + ky = 1 and 3x – 5y = 7 are parallel, then the value of k is

Answer
Answer: a
9. One equation of a pair of dependent linear equations is 2x + 5y = 3. The second equation will be
(a) 2x + 5y = 6
(b) 3x + 5y = 3
(c) -10x – 25y + 15 = 0
(d) 10x + 25y = 15
Answer
Answer: c
10. If x = a, y = b is the solution of the equations x + y = 5 and 2x – 3y = 4, then the values of a and b are respectively
(a) 6, -1
(b) 2, 3
(c) 1, 4
(d) 19/5, 6/5
Answer
Answer: d
11. The graph of x = -2 is a line parallel to the
(a) x-axis
(b) y-axis
(c) both x- and y-axis
(d) none of these
Answer
Answer: b
12. The graph of y = 4x is a line
(a) parallel to x-axis
(b) parallel to y-axis
(c) perpendicular to y-axis
(d) passing through the origin
Answer
Answer: d
13. The graph of y = 5 is a line parallel to the
(a) x-axis
(b) y-axis
(c) both axis
(d) none of these
Answer
Answer: a
14. Two equations in two variables taken together are called
(a) linear equations
(b) quadratic equations
(c) simultaneous equations
(d) none of these
Answer
Answer: c
15. If am bl then the system of equations ax + by = c, lx + my = n, has
(a) a unique solution
(b) no solution
(c) infinitely many solutions
(d) none of these
Answer
Answer: a
16. If in the equation x + 2y = 10, the value of y is 6, then the value of x will be
(a) -2
(b) 2
(c) 4
(d) 5
Answer
Answer: a
17. The graph of the equation 2x + 3y = 5 is a
(a) vertical line
(b) straight line
(c) horizontal line
(d) none of these
Answer
Answer: b
18. The value of k, for which equations 3x + 5y = 0 and kx + lOy = 0 has a non-zero solution is
(a) 6
(b) 0
(c) 2
(d) 5
Answer
Answer: a
19. The value of k, for which the system of equations x + (k + l)y = 5 and (k + l)x + 9y = 8k – 1 has infinitely many solutions is
(a) 2
(b) 3
(c) 4
(d) 5
Answer
Answer: a
20. The value of k for which the equations (3k + l)x + 3y = 2; (k2 + l)x + (k – 2)y = 5 has no solution, then k is equal to
(a) 2
(b) 3
(c) 1
(d) -1
Answer
Answer: d
21. The pair of equations x = a and y = b graphically represents lines which are
(a) parallel
(b) intersecting at (b, a)
(c) coincident
(d) intersecting at (a, b)
Answer
Answer: d
22. Asha has only ₹1 and ₹2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is ₹75, then the number of ₹1 and ₹2 coins are, respectively
(a) 35 and 15
(b) 15 and 35
(c) 35 and 20
(d) 25 and 25
Answer
Answer: d
23. The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. The present ages of the son and the father are, respectively
(a) 4 and 24
(b) 5 and 30
(c) 6 and 36
(d) 3 and 24
Answer
Answer: c
24. The sum of the digits of a two-digit number is 9. If 27 is added to it, the digits of the number get reversed. The number is
(a) 27
(b) 72
(c) 45
(d) 36
Answer
Answer: d
25. The pair of linear equations 2x + 3y = 5 and 4x + 6y= 10 is
(a) inconsistent
(b) consistent
(c) dependent consistent
(d) none of these
Answer/Explanation
Answer: c
Explaination:
![]()
26. The pair of equations y = 0 and v = -7 has [NCERT Exemplar Problems]
(a) one solution
(b) two solutions
(c) infinitely many solutions
(d) no solution
Answer/Explanation
Answer: d
Explaination: (d) No solution (parallel lines)
27. The pair of equations x = a and y = b graphically represents lines which are
(a) parallel
(b) intersecting at (b, a)
(c) coincident
(d) intersecting at (a, b)
Answer/Explanation
Answer: d
Explaination: (d) Intersecting at (a, b)
28. Match the Column:

(a) 1 – A, 2 – B, 3 – C
(b) 1 – B, 2 – C, 3 – A
(c) 1 – C, 2 – B, 3 – A
(d) 1 – A, 2 – C, 3 – B
Answer/Explanation
Answer: d
Explaination:

29. The pair of equations x = 4 and y = 3 graphically represents lines which are
(a) parallel
(b) intersecting at (3, 4)
(c) coincident
(d) intersecting at (4, 3)
Answer/Explanation
Answer: d
Explaination:
(d) When lines x = 4, y = 3 will intersect, then x coordinate = 4, y-coordinate = 3
30. a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, where a1, b1, c1, a2, b2, c2 are all real numbers and a12+ b12 ≠ 0, a22 + b22 ≠ 0, is called a
(a) family of two different straight lines
(b) family of two coincident lines
(c) pair of linear equations in two variables
(d) none of these
Answer/Explanation
Answer: c
Explaination:
(c) Definition of pair of linear equations in two variables.
31. Match the Column:

(a) 1 – A, 2 – B, 3 – C
(b) 1 – B, 2 – A, 3 – C
(c) 1 – B, 2 – C, 3 – A
(d) 1 – C, 2 – A, 3 – B
Answer/Explanation
Answer: c
Explaination:
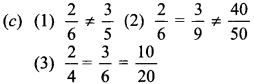
32. A pair of linear equations which has a unique solution x = 2, y = -3 is [NCERT Exemplar Problems]
(a) x + y = —1; 2x – 3y = -5
(b) 2x + 5y = -11; 4x + 10y = -22
(c) 2x – y = 1 ; 3x + 2y = 0
(d) x-4y- 14 = 0; 5x-y- 13 = 0
Answer/Explanation
Answer: b
Explaination:
(b) 2x + 5y = – 11; 4x + 10y = – 22
33. The father’s age is six times of his son’s age. Four years hence, the age of the father will be four times of his son’s age. The present ages, in years, of the son and the father are, respectively. [NCERT Exemplar Problems]
(a) 4 and 24
(b) 5 and 30
(c) 6 and 36
(d) 3 and 24
Answer/Explanation
Answer: c
Explaination:
Let F and S be the ages of father and sos respectively.
ATQ F = 6S …(i)
F + 4 = 4(S + 4)
⇒ F + 4 = 4S + 16 …(ii)
Substituting F = 6S in (ii), we get
6S + 4 = 4S + 16
2S = 12 .
⇒ S = 6; F = 36
34. If x = a, y = b is the solution of the pair of equations x – y = 2 and x + y = 4, then the respective values of a and b are
[CBSE 2018(C)]
(a) 3, 5
(b) 5, 3
(c) 3, 1
(d) -1, -3
Answer/Explanation
Answer: c
Explaination:
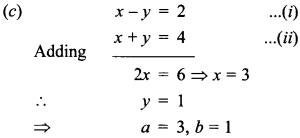
35. The difference between a two digit number and the number obtained by interchanging the digits is 27. What is the difference betw een the two digits of the number?
(a) 9
(b) 6
(c) 12
(d) 3
Answer/Explanation
Answer: d
Explaination:
Let number is 10x + y (x, y are the digits).
Number obtained by interchanging the digits = 10y+x
∴ 10x + y – (10y + x) = 27
9(x -y) = 27
∴ x – y = 3
36. The pair of equations ax + 2y = 7 and 3x + by = 16 represent parallel lines if
(a) a = b
(b) 3a = 2b
(c) 2 a = 3 b
(d) ab = 6
Answer/Explanation
Answer: c
Explaination:

37. The equations ax + by + c = 0 and dx + ey + c = 0 represent the same straight line if
(a) ad = be
(b) ac = bd
(c) be = ad
(d) ab = de
Answer/Explanation
Answer: d
Explaination:
![]()

38. Using the following equations:
\(\frac{4}{x}\) + 6y = 10
\(\frac{1}{x}\) – 6y = 5
find the value of p if p = 5x.
(a) 1
(b) 2
(c) 3
(d) 4
Answer/Explanation
Answer: a
Explaination:

39. Find the number of solutions of the following pair of linear equations:
x + 2y — 8 = 0
2x + 4 v =16
Answer/Explanation
Answer:
Explaination:
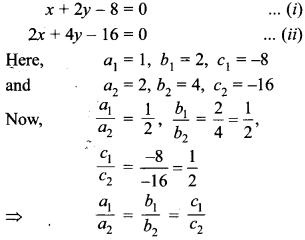
∴ Given pair of linear equations has infinite many solutions.
40. Write whether the following pair of linear equations is consistent or not. x + y = 14, x – y = 4
Answer/Explanation
Answer:
Explaination:

⇒ The equations have unique solution.
∴ Pair of linear equations is consistent.
41. Given the linear equation 3x + 4y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is parallel lines.
Answer/Explanation
Answer:
Explaination:
Lines are parallel when \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
∴ One of the linear equation in two variables can be 6x + 8y + k = 0 where k is constant not equal to -16.
42. Find the value of k for which the given pair of linear equations has no common solution.
4x + Ay = 5
8x + 12y = 10
Answer/Explanation
Answer:
Explaination:

43. Find the value of p for which the given pair of linear equations has infinite many solutions.
4x + 3y – 4=0
px + 9y + 12 = 0
Answer/Explanation
Answer:
Explaination:

44. The larger of two supplementary angles exceeds the smaller by 20 degrees. Find the angles.
Answer/Explanation
Answer: c
Explaination:
Let larger angle = x° and smaller angle =y° Now x -y = 20 andx +y = 180
∴ Algebraic representation is x – y = 20, x+y= 180
45. On solving the following pair of linear equations: 2x – y = 2; 5x + 2y = 14 by substitution method, values of x and y are _____ and _____ respectively.
Answer/Explanation
Answer:
Explaination:
2x – y = 2 …(i)
5x + 2y = 14 …(ii)
Substituting y = 2x – 2 in (ii), we get 5x + 2(2x – 2)=14
9x – 4 = 14
⇒ x= \(\frac{18}{9}\) = 2
⇒ x = 2, y = 2
46. Solve the following pair of linear equations by substitution method 2x – 3y +15 = 0; 3x – 5 = 0.
Answer/Explanation
Answer: c
Explaination:

47. There are two positive numbers such
that sum of twice the first and thrice the second is 39, while the sum of thrice the first and twice the second is 36. The larger of the two is _____ .
Answer/Explanation
Answer: c
Explaination:
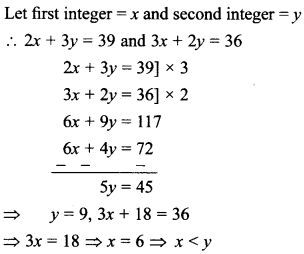
48. Solve for x and y by the method of elimination:
4x -3 y = 1; 5x – 7y = 2.
Answer/Explanation
Answer:
Explaination:
Given equations are
4x – 3y = 1 …(i)
5x – 7y = -2 …(ii)
For making coefficient of y equal in both the equations multiplying equation (/) with 7, we get
7 × (4x – 3y) = 7 × 1
⇒ 28x – 21y = 7 …(iii)
Multiplying equation (ii) with 3, we get
3 × (5x – 7y) = 3 × -2
⇒ 15x – 21y = -6 …(iv)
Subtracting equation (iv) from (iii), we get

when x – 1, equation (i) becomes
4 × – 3y = 1
⇒ -3y = -3
⇒ y = 1
∴ x= 1, y= 1
49. If the pair of equations x + y = √2 and x sin θ + y cos θ = 1 has infinitely many solutions, then θ = _____ .
Answer/Explanation
Answer:
Explaination:
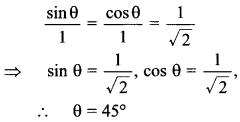
50. Find the value of k so that the following system of equation has infinite solutions: 3x – y – 5 = 0, 6x – 2y + k = 0
Answer/Explanation
Answer:
Explaination:

51. For which values of p, does the pair of equations given below has unique solution? 4x + py + 8 = 0 and 2x + 2y + 2 = 0
Answer/Explanation
Answer:
Explaination:
For unique solution, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \Rightarrow \frac{4}{2} \neq \frac{p}{2}\)
⇒ p ≠ 4
52. The equations \(\frac{x y}{x+y}=\frac{1}{9}\) and \(\frac{x y}{x-y}=\frac{1}{4}\) are equivalent to the equations:
![]()
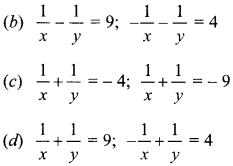
Answer/Explanation
Answer: d
Explaination:
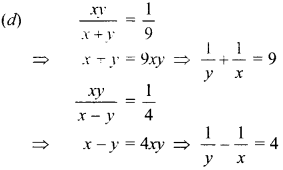
53. On solving the following equations: \(\frac{5}{x}\) + 6y = 3; \(\frac{-5}{x}\) + 3y = 6, values of x and y are ____ and ____ respectively.
Answer/Explanation
Answer:
Explaination:
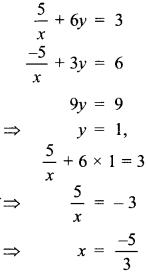
54. Solve forx andy : x + \(\frac{6}{y}\) = 6, 3x – \(\frac{8}{y}\) = 5
Answer/Explanation
Answer:
Explaination:
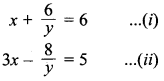
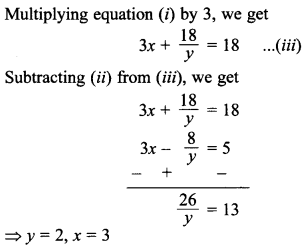
We hope the given MCQ Questions for Class 10 Maths Pair of Linear Equations in Two Variables with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.