Free PDF Download of CBSE Class 10 Maths Chapter 2 Polynomials Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Polynomials MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 2 Polynomials
1. If one zero of the quadratic polynomial x² + 3x + k is 2, then the value of k is
(a) 10
(b) -10
(c) 5
(d) -5
Answer
Answer: b
2. Given that two of the zeroes of the cubic poly-nomial ax3 + bx² + cx + d are 0, the third zero is

Answer
Answer: a
3. If one of the zeroes of the quadratic polynomial (k – 1) x² + kx + 1 is – 3, then the value of k is

Answer
Answer: a
4. A quadratic polynomial, whose zeroes are -3 and 4, is
(a) x²- x + 12
(b) x² + x + 12
(c) \(\frac{x^{2}}{2}-\frac{x}{2}-6\)
(d) 2x² + 2x – 24
Answer
Answer: c
5. If the zeroes of the quadratic polynomial x2 + (a + 1) x + b are 2 and -3, then
(a) a = -7, b = -1
(b) a = 5, b = -1
(c) a = 2, b = -6
(d) a – 0, b = -6
Answer
Answer: d
6. The number of polynomials having zeroes as -2 and 5 is
(a) 1
(b) 2
(c) 3
(d) more than 3
Answer
Answer: d
7. Given that one of the zeroes of the cubic polynomial ax3 + bx² + cx + d is zero, the product of the other two zeroes is

Answer
Answer: b
8. If one of the zeroes of the cubic polynomial x3 + ax² + bx + c is -1, then the product of the
other two zeroes is
(a) b – a + 1
(b) b – a – 1
(c) a – b + 1
(d) a – b – 1
Answer
Answer: a
9. The zeroes of the quadratic polynomial x2 + 99x + 127 are
(a) both positive
(b) both negative
(c) one positive and one negative
(d) both equal
Answer
Answer: b
10. The zeroes of the quadratic polynomial x² + kx + k, k? 0,
(a) cannot both be positive
(b) cannot both be negative
(c) are always unequal
(d) are always equal
Answer
Answer: a
11. If the zeroes of the quadratic polynomial ax² + bx + c, c # 0 are equal, then
(a) c and a have opposite signs
(b) c and b have opposite signs
(c) c and a have the same sign
(d) c and b have the same sign
Answer
Answer: c
12. If one of the zeroes of a quadratic polynomial of the form x² + ax + b is the negative of the other, then it
(a) has no linear term and the constant term is negative.
(b) has no linear term and the constant term is positive.
(c) can have a linear term but the constant term is negative.
(d) can have a linear term but the constant term is positive.
Answer
Answer: a
13. Which of the following is not the graph of quadratic polynomial?

Answer
Answer: d
14. The number of polynomials having zeroes as 4 and 7 is
(a) 2
(b) 3
(c) 4
(d) more than 4
Answer
Answer: d
15. A quadratic polynomial, whose zeores are -4 and -5, is
(a) x²-9x + 20
(b) x² + 9x + 20
(c) x²-9x- 20
(d) x² + 9x- 20
Answer
Answer: b
16. The zeroes of the quadratic polynomial x² + 1750x + 175000 are
(a) both negative
(b) one positive and one negative
(c) both positive
(d) both equal
Answer
Answer: a
17. The zeroes of the quadratic polynomial x² – 15x + 50 are
(a) both negative
(b) one positive and one negative
(c) both positive
(d) both equal
Answer
Answer: c
18. The zeroes of the quadratic polynomial 3x² – 48 are
(a) both negative
(b) one positive and one negative
(c) both positive
(d) both equal
Answer
Answer: b
19. The zeroes of the quadratic polynomial x² – 18x + 81 are
(a) both negative
(b) one positive and one negative
(c) both positive and unequal
(d) both equal and positive
Answer
Answer: d
20. The zeroes of the quadratic polynomial x² + px + p, p ≠ 0 are
(a) both equal
(b) both cannot be positive
(c) both unequal
(d) both cannot be negative
Answer
Answer: b
21. If one of the zeroes of the quadratic polynomial (p – l)x² + px + 1 is -3, then the value of p is
Answer
Answer: b
22. If the zeroes of the quadratic polynomial Ax² + Bx + C, C # 0 are equal, then
(a) A and B have the same sign
(b) A and C have the same sign
(c) B and C have the same sign
(d) A and C have opposite signs
Answer
Answer: b
23. If x3 + 1 is divided by x² + 5, then the possible degree of quotient is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
Answer: b
24. If x3 + 11 is divided by x² – 3, then the possible degree of remainder is
(a) 0
(b) 1
(c) 2
(d) less than 2
Answer
Answer: d
25. If x4 + 3x² + 7 is divided by 3x + 5, then the possible degrees of quotient and remainder are:
(a) 3, 0
(b) 4, 1
(c) 3, 1
(d) 4, 0
Answer
Answer: a
26. If x5 + 2x4 + x + 6 is divided by g(x), and quotient is x² + 5x + 7, then the possible degree of g(x) is:
(a) 4
(b) 2
(c) 3
(d) 5
Answer
Answer: c
27. If x5 + 2x4 + x + 6 is divided by g(x) and quo-tient is x² + 5x + 7, then the possible degree of remainder is:
(a) less than 1
(b) less than 2
(c) less than 3
(d) less than 4
Answer
Answer: c
28. What is the number of zeroes that a linear poly-nomial has/have:
(a) 0
(b) 1
(c) 2
(d) 3
Answer
Answer: b
29. What is the number(s) of zeroes that a quadratic polynomial has/have:
(a) 0
(b) 1
(c) 2
(d) 3
Answer
Answer: c
30. What is the number(s) of zeores that a cubic polynomial has/have:
(a) 0
(b) 1
(c) 2
(d) 3
Answer
Answer: d
31. If one of the zeroes of the cubic polynomial x3 + px² + qx + r is -1, then the product of the other two zeroes is
(a) p + q + 1
(b) p-q- 1
(c) q – p + 1
(d) q – p – 1
Answer
Answer: c
32. If one zero of the quadratic polynomial x² + 3x + b is 2, then the value of b is
(a) 10
(b) -8
(c) 9
(d) -10
Answer
Answer: d
33. If 1 is one of the zeroes of the polynomial x² + x + k, then the value of k is:
(a) 2
(b) -2
(c) 4
(d) -4
Answer
Answer: b
34. If p(x) is a polynomial of at least degree one and p(k) = 0, then k is known as
(a) value of p(x)
(b) zero of p(x)
(c) constant term of p{x)
(d) none of these
Answer/Explanation
Answer: b
Explaination:
Zero of p(x)
Let p(x) = ax + b
Put x = k
p(k) = ak + b = 0
∴ k is zero of p(x).
35. If one of the zeroes of the quadratic polynomial (k -1)x² + kx + 1 the value of k is [NCERT Exemplar Problems]

Answer/Explanation
Answer: c
Explaination:
(k – 1)² + kx + 1
One zero is – 3, so it must satisfy the equation and make it zero.
∴ (k- 1) (- 3)² + k(-3) + 1 =0
⇒ 9k – 9 – Ik + 1 = 0
⇒ 6k – 8 = 0
⇒ k = \(\frac{8}{6}\) = \(\frac{4}{3}\)
36. If the zeroes of the quadratic polynomial x² + (a + 1) x + b are 2 and -3, then [NCERT Exemplar Problem, CBSE 2011]
(a) a = -7, b = -1
(b) a = 5, b = -1
(c) a = 2, b = -6
(d) a = 0, b = -6
Answer/Explanation
Answer: d
Explaination:
x² + (a + 1)x + b
∵ x = 2 is a zero
and x = – 3 is another zero
∴ (2)² + (a + 1)² + 6 = 0
and (- 3)² + (a + 1) (- 3) + b = 0
⇒ 4 + 2cr + 2 + & = 0
and 9 – 3a – 3 + b = 0
⇒ 2a + b = – 6 …(i)
and – 3a + b = – 6 …(ii)
Solving (i) and (ii), we get 5a = 0
⇒ a = 0 and b = – 6.
37. Which of the following is not the graph of a quadratic polynomial?[NCERT Exemplar Problems]

Answer/Explanation
Answer: a
Explaination:
∵ It crosses the x-axis in three points.
38. Zeroes of a polynomial can be determined graphically. No. of zeroes of a polynomial is equal to no. of points where the graph of polynomial
(a) intersects y-axis
(b) intersects x-axis
(c) intersects y-axis or intersects x-axis
(d) none of these
Answer/Explanation
Answer: b
Explaination:
(b) Intersects x-axis.
39. If graph of a polynomial does not intersects the x-axis but intersects y-axis in one point, then no. of zeroes of the polynomial is equal to
(a) 0
(b) 1
(c) 0 or 1
(d) none of these
Answer/Explanation
Answer: a
Explaination:
(a) Zero
40. A polynomial of degree n has
(a) only 1 zero
(b) at least n zeroes
(c) atmost n zeroes
(d) more than n zeroes
Answer/Explanation
Answer: c
Explaination:
Maximum number of zeroes of a
polynomial = degree of the polynomial.
41. If p(x) = axr + bx + c, then –\(\frac{b}{a}\) is equal to
(a) 0
(b) 1
(c) product of zeroes
(d) sum of zeroes
Answer/Explanation
Answer: d
Explaination:
(d) Sum of zeroes = –\(\frac{b}{a}\)
42. If p(x) = ax² + bx + c one zero is and a + b + c = 0, then one zero is
(a) \(\frac{-b}{a}\)
(b) \(\frac{c}{a}\)
(c) \(\frac{b}{c}\)
(d) none of these
Answer/Explanation
Answer: b
Explaination:
p(1) = 0; a(1)² + b(1) + c = 0
⇒ a + b + c = 0
∴ one zero (α) = 1
αβ = product of zeroes = \(\frac{c}{a}\)
⇒ 1.β = \(\frac{c}{a}\)
⇒ β = \(\frac{c}{a}\)
∴ zeroes are 1 and \(\frac{c}{a}\)
43. If p{x) = ax2 + bx + one of the zeroes is c and a + c = b, then

Answer/Explanation
Answer: c
Explaination:
p(-1) = 0; a(-1)² + b(-1) + c = 0
⇒ a – b + C = 0,
∴ One zero (a) = -1
αα = product of zeroes = \(\frac{c}{a}\)
⇒ (-1).β = \(\frac{c}{a}\)
⇒ β = \(\frac{-c}{a}\)
44. The number of polynomials having zeroes as -2 and 5 is [NCERT Exemplar Problems]
(a) 1
(b) 2
(c) 3
(d) more than 3
Answer/Explanation
Answer: d
Explaination:
∵ x² – 3x – 10, 2x² – 6x – 20,
\(\frac{1}{2}\)x² – \(\frac{3}{2}\)x – 5, 3x² – 9x – 30 etc.,
have zeroes – 2 and 5.
45. Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeroes is [NCERT Exemplar Problems]

Answer/Explanation
Answer: b
Explaination:
∵ αβ + βγ + γα = \(\frac{c}{a}\)
Let, α = 0
So, 0 + βγ + 0 = \(\frac{c}{a}\)
⇒ βγ= \(\frac{c}{a}\)
46. If one of the zeroes of a quadratic polynomial of the form x² + ax + b is the negative of the other, then it
(a) has no linear term and the constant term is negative.
(b) has no linear term and the constant term is positive.
(c) can have a linear term but the constant term is negative.
(d) can have a linear term but the constant term is positive.
Answer/Explanation
Answer: a
Explaination:
f(x) = x² + ax + b
Given: zeroes are α and – α
Sum of zeroes = α – α = 0
∴ f(x) = x² + b, which is not linear
Product of zeroes = α(-α) = – α² = \(\frac{b}{1}\)
⇒ -α² = b
It is possible when, b < 0.
Hence, it has no linear term and the constant term is negative.
47. If 4x² – 6x – m is divisible by x – 3, the value of m is exact divisor of
(a) 9
(b) 45
(c) 20
(d) 36
Answer/Explanation
Answer: a
Explaination:
Here p(3) = 0
⇒ 4(3)² – 6 × 3-m = 0
⇒ 36 – 18 – m = 0
⇒ m=18
∴ Value of m is exactly divisible by 9.
48. Which one of the following statements is correct
(a) if x6 + 1 is divided by x + 1, then the remainder is -2.
(b) if x6 + 1 is divided by x – 1, then the remainder is 2.
(c) if x6 + 1 is divided by x + 1, then the remainder is 1.
(d) if x6 + 1 is divided by x – 1, then the remainder is -1.
Answer/Explanation
Answer: b
Explaination:
p(x) = x6 + 1
when divided by x – 1, then remainder = p(1)
∴ p(1) = 16 + 1 = 2
49. Consider the following statements
(i) x – 2 is a factor of x3 – 3x² + 4x – 4.
(ii) x + 1 is a factor of 2x3 + 4x + 6.
(iii) x – 1 is a factor of x5 + x4 – x3 + x² -x + 1.
In these statements
(a) 1 and 2 are correct
(b) 1, 2 and 3 are correct
(c) 2 and 3 are correct
(d) 1 and 3 are correct
Answer/Explanation
Answer: a
Explaination:
x – 2 is a factor of x3 – 3x² + 4x – 4
∵ remainder is zero Similarly x + 1 is a factor of 2x3 + 4x + 6
but x – 1 is not a factor of x5 + x4 – x3 + x² – x + 1
∵ remainder is not zero
∴ Statements 1 and 2 are correct.
50. If f(x) = 5x – 10 is divided by x – √2, then the remainder will be
(a) non zero rational number
(b) an irrational number
(c) 0
(d) \(f\left(\frac{1}{\sqrt{2}}\right)\)
Answer/Explanation
Answer: b
Explaination:
Remainder = f(√2) = 5 × √2 – 10
= an irrational number
51. Zeroes of p(z) = z² – 27 are ______ and ______ .
Answer/Explanation
Answer:
Explaination:
For zeroes z² – 27 = 0
⇒ z² = 27
⇒ z = ±√27
⇒ z = ± 3√3
52. Verify that x = 3 is a zero of the polynomial. p(x) = 2x3 – 5x² – 4x + 3
Answer/Explanation
Answer:
Explaination:
Here p(x) = 2x3 – 5x² – 4x + 3
∴ p{3) = 2(3)3 – 5 x (3)² -4 x 3 + 3
= 54 – 45- 12 + 3 = 0
∵ P(3) = 0
∴ x = 3 is a zero of p(x)
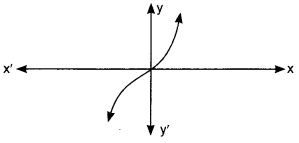
53. The graph of y =f(x) is given below. How many zeroes are there of f(x)?
Answer/Explanation
Answer:
Explaination:
Graph of y = f(x) intersect x-axis in one point only.
Therefore number of zeroes of f(x) is one.
54. The graph of y = f(x) is given, how many zeroes are there of f(x)?

Answer/Explanation
Answer:
Explaination:
∵ Graph y =f(x) does not intersect x-axis.
∴ f(x) has no zeroes.
55. The graph of y = f(x) is given below, for some polynomial f(x). Find the number of zeroes of f(x).

Answer/Explanation
Answer:
Explaination:
∵ Graph of f(x) intersects x-axis at three different points.
∴ Number of zeroes of f(x) = 3.
56. The graph of x = p(y) is given below, for some polynomial p(y). Find the number of zeroes of p(y).

Answer/Explanation
Answer:
Explaination:
∵ Graph of p(y) intersects y-axis in four different points.
∴ Numbers of zeroes = 4
57.
Graph of the polynomial p(x) =px² + 4x – 4 is given as above. Find the value of p.
Answer/Explanation
Answer:
Explaination:
Graph of p(x) touches the x-axis at (2, 0)
∴ x = 2 is a zero of the p(x)
⇒ p(2) = 0
⇒ p(2)² + 4 × 2 – 4 = 0
4p + 4 = 0
⇒ p = -1
58. If the product of the zeroes of x2 – 3kx + 2k1 – 1 is 7, then values of k are _____ and _____ .
Answer/Explanation
Answer:
Explaination:
Product of zeroes = 7
⇒ 2k² – 1 = 7
⇒ 2k² = 8
⇒ k² = 4
⇒ k = ± 2
59. If zeroes ofp(x) = 2x² -Ix + k are reciprocal of each other, then value of k is _____ .
Answer/Explanation
Answer:
Explaination:
∵ Zeroes are reciprocal of each other
∴ Product of zeroes = 1
⇒ \(\frac{k}{2}\) = 1
⇒ k = 2
60. Find the product of the zeroes of – 2x² + kx + 6.
Answer/Explanation
Answer:
Explaination:
Here a = – 2, b = k, c = 6
Product of zeroes = \(\frac{c}{a}\)
i. e., α × β = \(\frac{6}{-2}\) = -3
61. Find the sum of the zeroes of the given quadratic polynomial -3x² + k.
Answer/Explanation
Answer:
Explaination:
Since polynomial is -3x² + 0x + k
∴ a = -3, b = 0, c = k
and sum of zeroes = \(\frac{-b}{a}\)
i. e., α + β = \(\frac{-b}{a}\)
⇒ α + β = \(\frac{0}{-3}\) = 0
62. If one zero of the polynomial x² -4x+ 1 is 2 + √3, write the other zero.
Answer/Explanation
Answer:
Explaination:
Let other zero be α ,
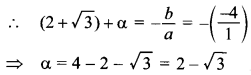
63. Write the polynomial, the product and sum of whose zeroes are –\(\frac{9}{2}\) and –\(\frac{3}{2}\) respectively.
Answer/Explanation
Answer:
Explaination:

64. The value of m, in order that x² – mx – 2 is the quotient where x3 + 3x² – 4 is divided by x + 2 is ____ .
Answer/Explanation
Answer:
Explaination:

Since quotient = x² – mx – 2
∴ x² – mx – 2 = x² + x – 2
On comparison of coefficient of x, we get m = – 1.
65. If one factor of x3 + 7kx² – 4kx + 12 is (x + 3), then the value of k is ______ .
Answer/Explanation
Answer:
Explaination:
p(x) = x3 + Ike – 4kx + 12
p(-3) = (-3)3 + 7k(-3)² – 4k (- 3) + 12
∵ x + 3 is a factor
∴ p(-3) = 0
⇒ -27 + 63k + 12k+ 12 = 0
⇒ 75k – 15 = 0
⇒ k = \(\frac{1}{2}\)
66. A polynomial of degree five is divided by a quadratic polynomial. If it leaves a remainder, then find the degree of remainder.
Answer/Explanation
Answer:
Explaination:
Degree of remainder is always less than divisor.
∴ Degree of remainder will be less than 2.
Hence, degree is 1 or 0.
67. Check whether 3x – 7 is a factor of polynomial 6x3 + x² – 26x – 25?
Answer/Explanation
Answer:
Explaination:

68. If x3 + x² – ax + b is divisible by x² – x, write the values of a and b.
Answer/Explanation
Answer:
Explaination:
∵ p(x) = x3+xl-ax + b is divisible by x² -x.
x (x – 1) is a factor of p(x).
⇒ x = 0 and x = 1 are zeroes of p(x).
⇒ p(0) = 0
⇒ (0)3 + (0)² – a × 0 + b = 0
⇒ b = 0 and p(1) = 0
⇒ 13 + (1)² – a × 1 + b = 0
⇒ 2 – a + 0 — 0
⇒ a = 2
We hope the given MCQ Questions for Class 10 Maths Polynomials with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 2 Polynomials Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.