Maths MCQs for Class 12 with Answers Chapter 4 Determinants

Free PDF Download of CBSE Maths Multiple Choice Questions for Class 12 with Answers Chapter 4 Determinants. Maths MCQs for Class 12 Chapter Wise with Answers PDF Download was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Determinants MCQs Pdf with Answers to know their preparation level.

Determinants Class 12 Maths MCQs Pdf

1.

Answer/Explanation

Answer: d
Explaination:

---

2.

Answer/Explanation

Answer: a
Explaination: (a), Δ = 6(-1)- 1(1) = -7.

---

3.

Answer/Explanation

Answer: d
Explaination:

---

4. Let A be a square matrix of order 2 × 2, then |KA| is equal to
(a) K|A|
(b) K²|A|
(c) K³|A|
(d) 2K|A|

Answer/Explanation

Answer: b
Explaination:

---

5.

Answer/Explanation

Answer: a
Explaination:

---

6. Let x, yeR, then the determinant

Answer/Explanation

Answer: a
Explaination:

---

7.

Answer/Explanation

Answer: d
Explaination: (d), as value of determinant is sum of the product of elements of any row and column and then- respective cofactor.

---

8. A and B are invertible matrices of the same order such that |(AB)^-1| = 8, If |A| = 2, then |B| is
(a) 16
(b) 4
(c) 6
(d) \(\frac{1}{16}\)

Answer/Explanation

Answer: d
Explaination:

---

9. Determinant is a number associated to a matrix, state true or false.

Answer/Explanation

Answer:
Explaination: False, as determinant is a number associated to a square matrix.

---

10.

Answer/Explanation

Answer:
Explaination: (a + ib) (a – ib) – (c + id) (c – id) = a² + b² – c² – d².

---

11.

Answer/Explanation

Answer:
Explaination:
sin 30° cos 60° + cos 30° sin 60°
= sin(30° + 60°) = sin 90° = 1.

---

12.

Answer/Explanation

Answer:
Explaination:
18x + 45 – 15x -6 = 0
⇒ 3x = -39
⇒ x = -13.

---

13. Evaluate the determinant

Answer/Explanation

Answer:
Explaination:

---

14.

Answer/Explanation

Answer:
Explaination:

---

15. Value of determinant

is 0, state true or false.

Answer/Explanation

Answer:
Explaination: True, as on performing C₃ → C₃ + C₂ we notice elements of C₁ and C₃ are proportional.

---

16. If A is a matrix of order 3 × 3, then |KA| = _______ .

Answer/Explanation

Answer:
Explaination:

---

17. The determinant

Answer/Explanation

Answer:
Explaination:

---

18. Evaluate the determinant

Answer/Explanation

Answer:
Explaination:

---

19. What is the value of the following determinant?

Answer/Explanation

Answer:
Explaination:

---

20. If for any 2 × 2 square matrix A, A(adj A)

Answer/Explanation

Answer:
Explaination:

---

21. If area of a triangle with vertices (3, 2), (-1,4) and (6, k) is 7 sq units, then possible values of k are ______ .

Answer/Explanation

Answer:
Explaination:

---

22. The points (a + 5, a – 4), (a – 2, a + 3) and (a, a) are non-collinear for any value of a. State true or false.

Answer/Explanation

Answer:
Explaination:

---

23. Find the area of the triangle with vertices (-1, 2), (4, 0) and (3, 9).

Answer/Explanation

Answer:
Explaination:

---

24. Find the value of x, such that the points (0, 2), (1, x) and (3, 1) are collinear.

Answer/Explanation

Answer:
Explaination:

---

25. Show that points A(a, b + c), B(b, c + a) and C(c, a + b) are collinear. [NCERT]

Answer/Explanation

Answer:
Explaination:

---

26. Find the cofactor of a₁₂ of the determinant

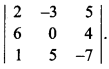
Answer/Explanation

Answer:
Explaination:

---

27.

cofactor of the element a₂₁ [Foreign 2015]

Answer/Explanation

Answer:
Explaination: Cofactor of a2l = (-1)³ (18 – 21) = 3

---

28. In the determinant
find
(i) minor of element 3
(ii) cofactor of element 5.

Answer/Explanation

Answer:
Explaination:

---

29. If A and B are invertible matrices of the same order (AB)^-1 is _____ .

Answer/Explanation

Answer:
Explaination:

---

30.

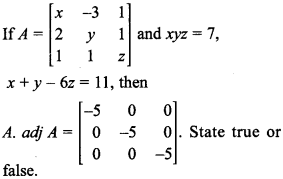
Answer/Explanation

Answer:
Explaination:

---

31. A is invertible matrix of order 3 × 3 and |A| = 9, then value of |A^-1|is

Answer/Explanation

Answer:
Explaination:

---

32. If the value of a third order determinant is 7, then the value of a determinant formed by replacing each element by its cofactor will be 49. State true or false.

Answer/Explanation

Answer:
Explaination: True, as |adj.A| = |A|^n-1, A is matrix of order 3 × n

---

33. Inverse of matrix

exists, state true or false.

Answer/Explanation

Answer:
Explaination:

---

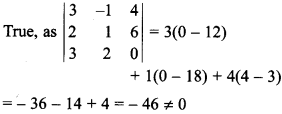
34. For what value of k, the matrix \(\left[\begin{array}{ll}{k} & {2} \\ {3} & {4}\end{array}\right]\) has no inverse?

Answer/Explanation

Answer:
Explaination:

---

35. Write A^-1 for A = \(\left[\begin{array}{ll}{2} & {5} \\ {1} & {3}\end{array}\right]\) [Delhi 2011]

Answer/Explanation

Answer:
Explaination:

---

36. Given a square matrix A of order 3 × 3, such that |A| = 12, find the value of |A. adj A|. [HOTS]

Answer/Explanation

Answer:
Explaination:
|A adj A| = |A|³ as matrix A is of order 3 × 3.
∴ |A adj A| = |A|³ = (12)³ = 1728

---

37. If A is a 3 × 3 invertible matrix, then what will be the value of k if det(A^-1) = (det A)^k

Answer/Explanation

Answer:
Explaination:

---

38.

Answer/Explanation

Answer:
Explaination:

---

39. If for any 2 × 2 square matrix A, A(adj A) = \(\left[\begin{array}{ll}{8} & {0} \\ {0} & {8}\end{array}\right]\), then write the value of |A|. [Delhi 2017]

Answer/Explanation

Answer:
Explaination:

---

40.

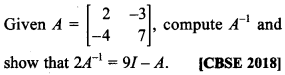
Answer/Explanation

Answer:
Explaination:

---

We hope the given Maths MCQs for Class 12 with Answers Chapter 4 Determinants will help you. If you have any query regarding CBSE Class 12 Maths Determinants MCQs Pdf, drop a comment below and we will get back to you at the earliest.