Free PDF Download of CBSE Maths Multiple Choice Questions for Class 12 with Answers Chapter 2 Inverse Trigonometric Functions. Maths MCQs for Class 12 Chapter Wise with Answers PDF Download was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Inverse Trigonometric Functions MCQs Pdf with Answers to know their preparation level.
Inverse Trigonometric Functions Class 12 Maths MCQs Pdf
1. Principal value of sin-1 \(\frac{1}{2}\) is

Answer/Explanation
Answer: d
Explaination:

2. sin-1{sin (\(\frac{2 \pi}{3}\))} = \(\frac{2 \pi}{3}\), state true or false.
Answer/Explanation
Answer:
Explaination: False, as –\(\frac{\pi}{2}\) ≤ sin<sup>-1</sup> x ≤ \(\frac{\pi}{2}\).
3. tan-1{sin (-\(\frac{\pi}{2}\))} is equal to
(a) -1
(b) 1
(c) \(\frac{\pi}{2}\)
(d) –\(\frac{\pi}{4}\)
Answer/Explanation
Answer: d
Explaination:
(d), as sin (-\(\frac{\pi}{2}\))= -1, and tan<sup>-1</sup>(-1) = – \(\frac{\pi}{4}\).
4. sec{tan-1 (-\(\frac{y}{3}\))} is equal to

Answer/Explanation
Answer: b
Explaination:
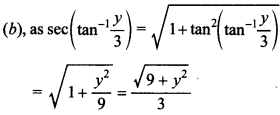
5. Principal branch of tan-1 x is ______ .
Answer/Explanation
Answer:
Explaination:
![]()
6. Principal value of the expression cos-1[cos(-680°)] is

Answer/Explanation
Answer: a
Explaination:
(a), as cos(-680°) = cos 680°
= cos(720° – 40°) = cos 40°
∴ cos<sup>-1</sup>[cos(-680°)J = cos<sup>-1</sup> (cos 40°)
= 40° = \(\frac{2 \pi}{9}\).
7. If tan-1x = sin-1(\(\frac{1}{\sqrt{2}}\)),then x is ______ .
Answer/Explanation
Answer:
Explaination: 1, as tan<sup>-1</sup> x = \(\frac{\pi}{4}\).
8. cos-1 \(\left(\cos \frac{7 \pi}{6}\right)=\frac{7 \pi}{6}\), state true or false.
Answer/Explanation
Answer:
Explaination: False, as \(\frac{7 \pi}{6}\) ∉ [0, π].
9. Find the value of tan-1 √3 – cot-1(-√3). [CBSE 2018]
Answer/Explanation
Answer:
Explaination:

10. Find the principal value of cos-1 \(\frac{1}{2}\).
Answer/Explanation
Answer:
Explaination:
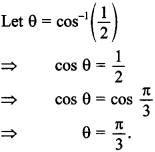
11. Find the principal value of
![]()
Answer/Explanation
Answer:
Explaination:
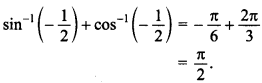
12. What is the domain of the function sin-1 x?
Answer/Explanation
Answer:
Explaination: -1 ≤ x ≤ 1 or [-1, 1]
13. Find the value of sin\(\left[\frac{\pi}{3}-\sin ^{-1}\left(-\frac{1}{2}\right)\right]\). [NCERT; Delhi 2011]
Answer/Explanation
Answer:
Explaination:


14. Find the principal value of tan-1√3 sec-1(-2). [NCERT; AI 2012]
Answer/Explanation
Answer:
Explaination:
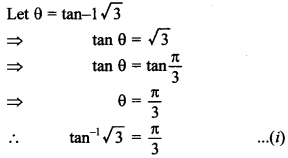
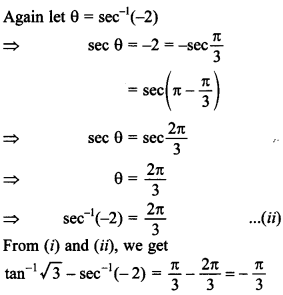
15. If sin-1 x = \(\frac{\pi}{10}\), for some x ∈ R, then the value of cos-1 is ______ .
Answer/Explanation
Answer:
Explaination:

16. If tan-1 x -cot-1 = \(\frac{\pi}{6}\), then x is ______ .
Answer/Explanation
Answer:
Explaination:
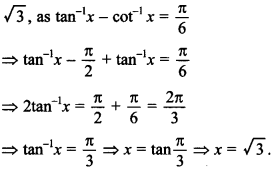
17. The domain of the function^ = sin’ -‘(V) is
(a) [0, 1]
(b) (0, 1)
(c) [-1, 1]
(d) Φ
Answer/Explanation
Answer: c
Explaination:
(c), as -1 ≤ -x² < 1
⇒ 1 ≥ x² ≥ -1
⇒ 0 ≤ x² ≤ 1
⇒ |x| ≤ 1
⇒ -1 ≤ x ≤ 1.
18. If sec-1 x + sec-1 y = \(\frac{\pi}{2}\) the value of cosec-1x + cosec-1y is

Answer/Explanation
Answer: b
Explaination:

19. The value of tan²(sec-12) + cot2(cosec-13) is
(a) 5
(b) 11
(c) 13
(d) 15
Answer/Explanation
Answer: b
Explaination:
(b), as tan²(sec<sup>-1</sup>2) + cot²cosec<sup>-1</sup>3)
= sec²(sec<sup>-1</sup>2) – 1 + cosec²(cos 3) – 1
= (2)² – 1 +(3)² – 1
= 4 – 1 +9 – 1 = 11.
20. cot(\(\frac{\pi}{4}\) – 2 cot-13) = 7, state true or false.
Answer/Explanation
Answer:
Explaination:

21. If 3 sin-1x + cos-1x = π, then x is equal to

Answer/Explanation
Answer: b
Explaination:
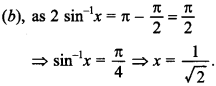
22.

Answer/Explanation
Answer:
Explaination:

23. If cos(tan-1x + cot-1√3) = 0, then value of x is _____ .
Answer/Explanation
Answer:
Explaination: √3, as tan-1x + cot-1 √3 = \(\frac{\pi}{2}\)
⇒ x = √3
24. If sin-1x + sin-1y + sin-1z = then the value of x + y² + z3 is
(a) 1
(b) 3
(c) 2
(d) 5
Answer/Explanation
Answer: b
Explaination:
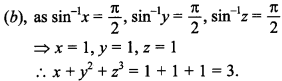
25. The domain of y = cos-1(x² – 4) is
(a) [3, 5]
(b) [0, π]
(c) [-√5 ,-√3] ∩ [-√5,√3]
(d) [-√5 ,-√3] ∪ [√3, √5]
Answer/Explanation
Answer:
Explaination:

26. Show that sin-1(2x\(\sqrt{1-x^{2}}\)) = 2 sin-1 – \(\frac{1}{\sqrt{2}}\) ≤ x ≤ \(\frac{1}{\sqrt{2}}\)
Answer/Explanation
Answer:
Explaination:

27. Find the value of sec(tan-1 –\(\frac{1}{2}\)).
Answer/Explanation
Answer:
Explaination:

28. If sin(sin-1\(\frac{1}{5}\) + cos-1x) = 1 then find the value of x. [NCERT; HOTS; Delhi 2014]
Answer/Explanation
Answer:
Explaination:

29. Find the value of
![]() [NCERT; Delhi 2013 (C), 2011]
[NCERT; Delhi 2013 (C), 2011]
Answer/Explanation
Answer:
Explaination:

30.
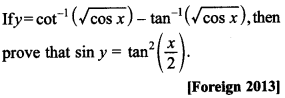
Answer/Explanation
Answer:
Explaination:


31. Prove that 3 sin-1 x = sin-1(3x – 4x3),
![]()
Answer/Explanation
Answer:
Explaination:
Let x = sin θ
=> θ = sin-1x
RHS = sin-1(3x – 4x3)
= sin--1 [3 sin θ – 4 sin3 θ]
= sin-1 [sin 3θ] = 3θ = 3 sin-1x = LHS
32. Prove that sin-1x = tan-1\(\left(\frac{x}{\sqrt{1-x^{2}}}\right)\)
Answer/Explanation
Answer:
Explaination:

33.

Answer/Explanation
Answer:
Explaination:
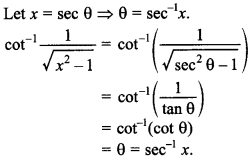
34. If sin-1x + sin-1y = \(\frac{2 \pi}{3}\), then find the value of cos-1x + cos-1y.
Answer/Explanation
Answer:
Explaination:

35. Find the value oftan(2 tan-1 \(\frac{1}{5}\)). [Delhi 2013]
Answer/Explanation
Answer:
Explaination:

We hope the given Maths MCQs for Class 12 with Answers Chapter 2 Inverse Trigonometric Functions will help you. If you have any query regarding CBSE Class 12 Maths Inverse Trigonometric Functions MCQs Pdf, drop a comment below and we will get back to you at the earliest.