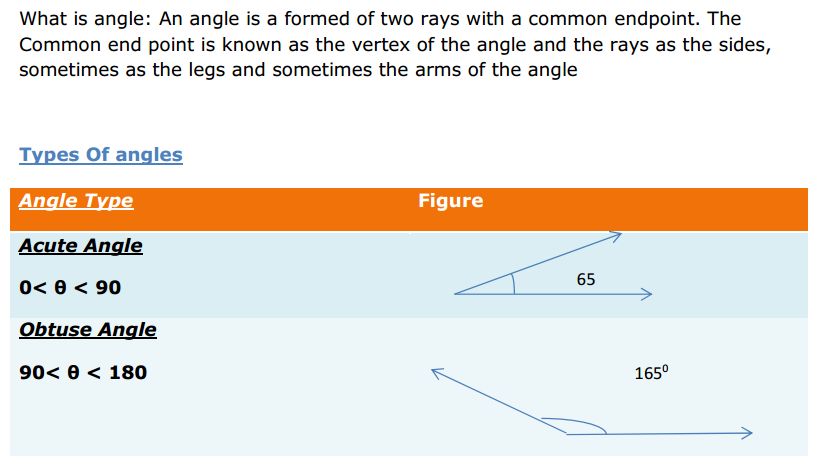
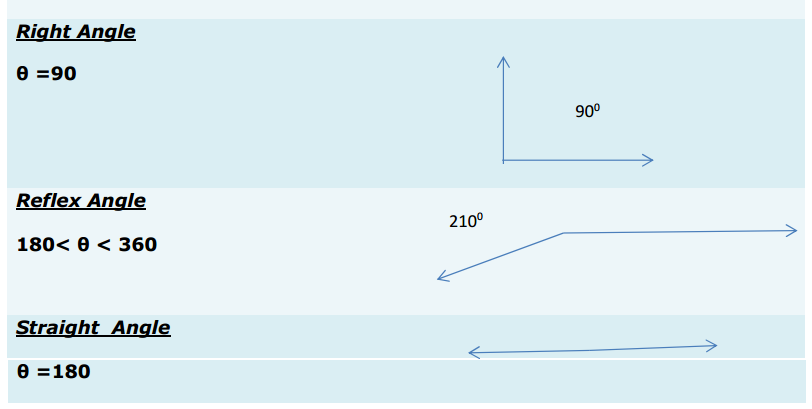
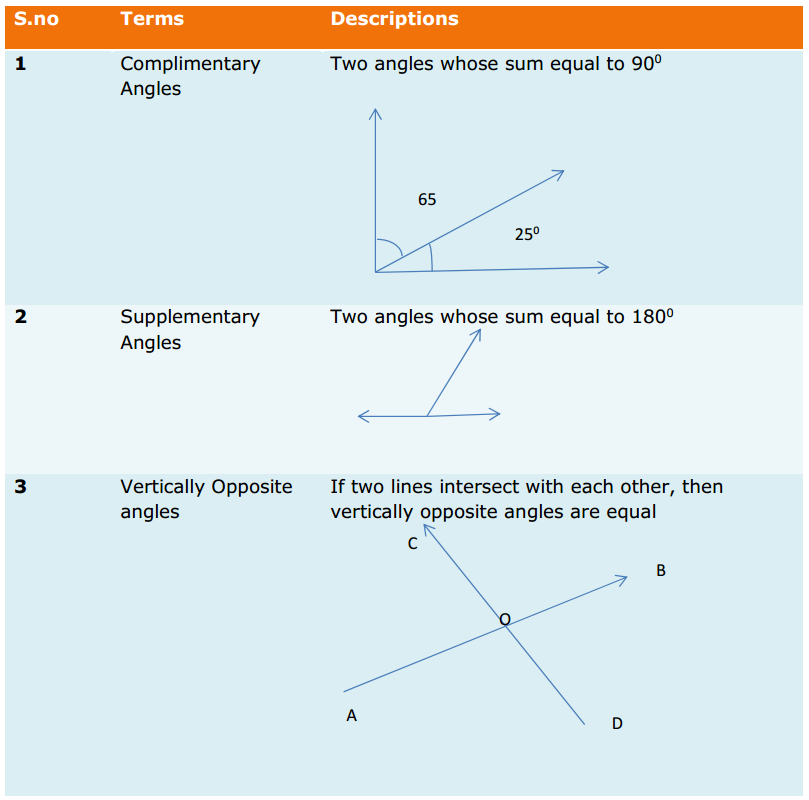
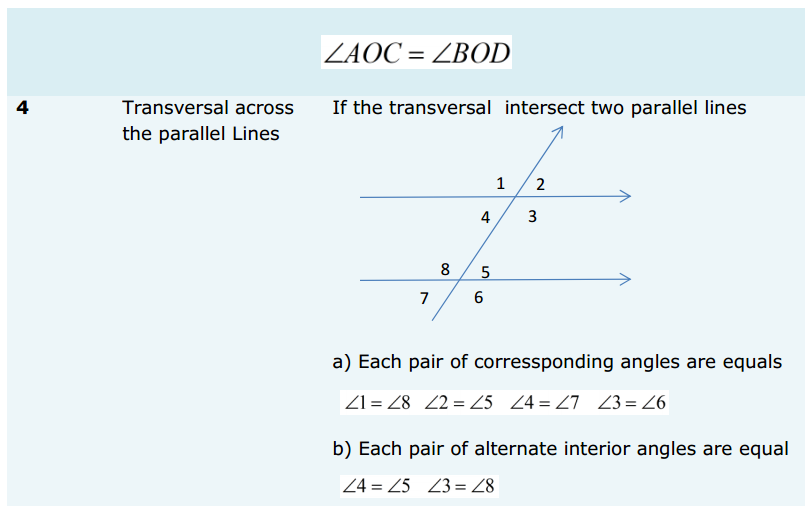
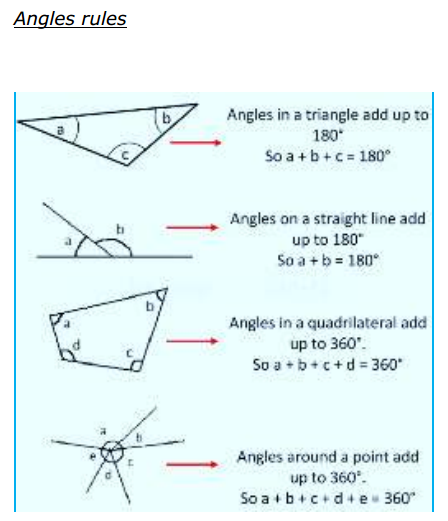
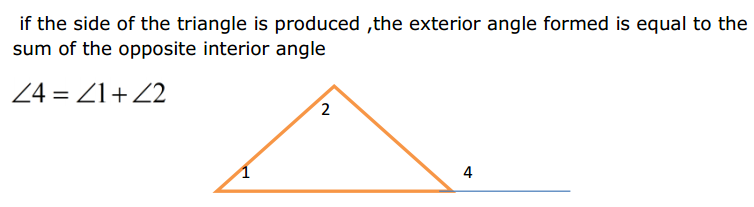
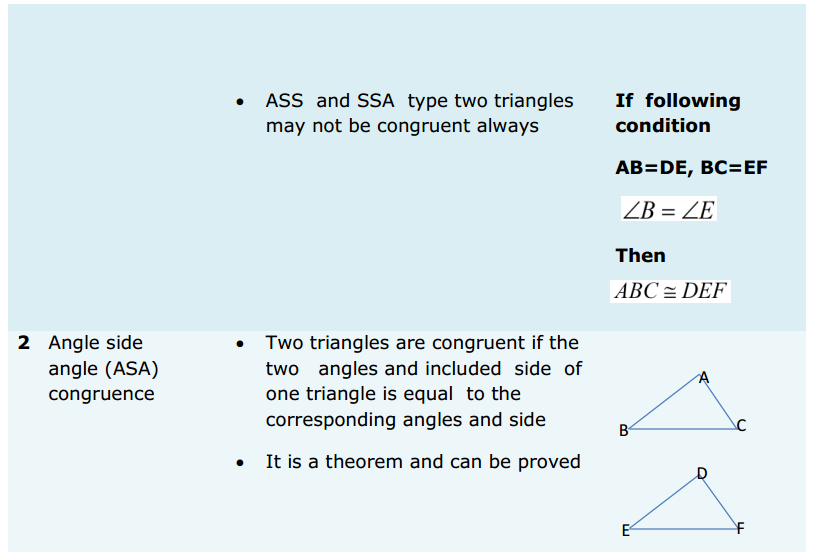
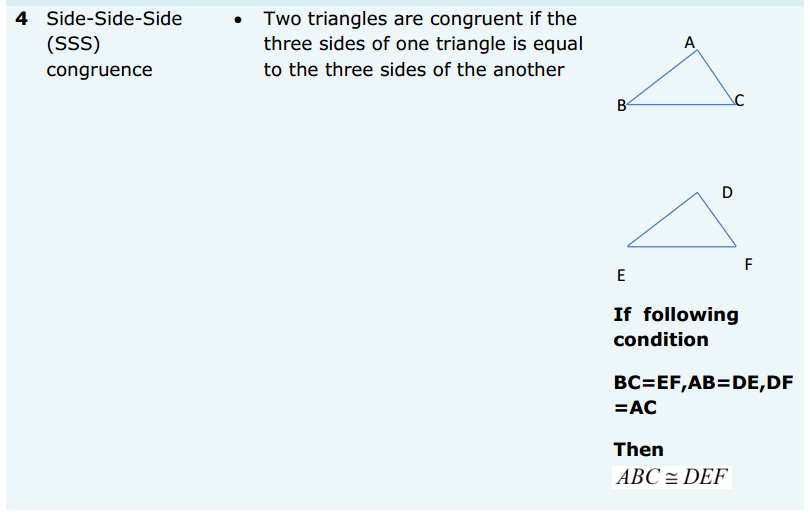
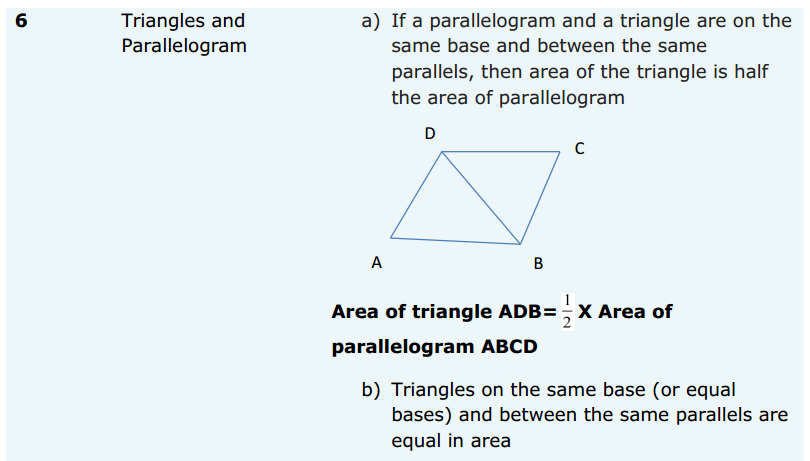
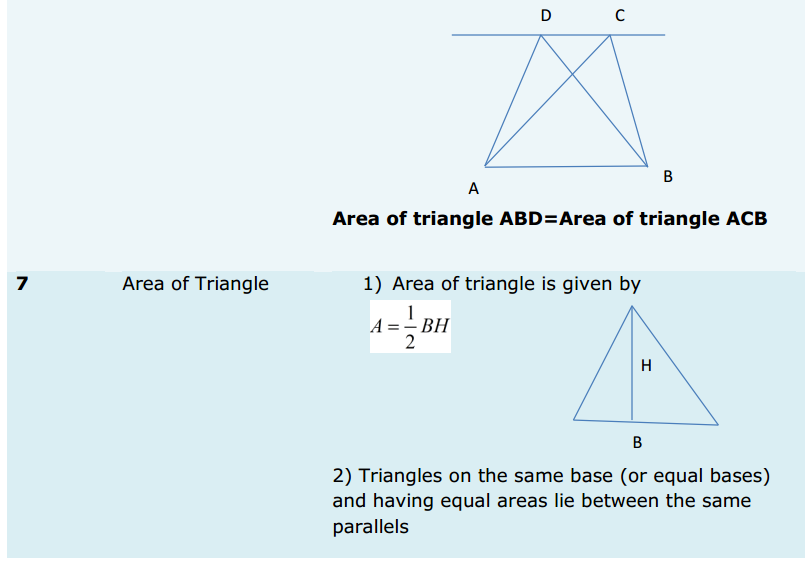
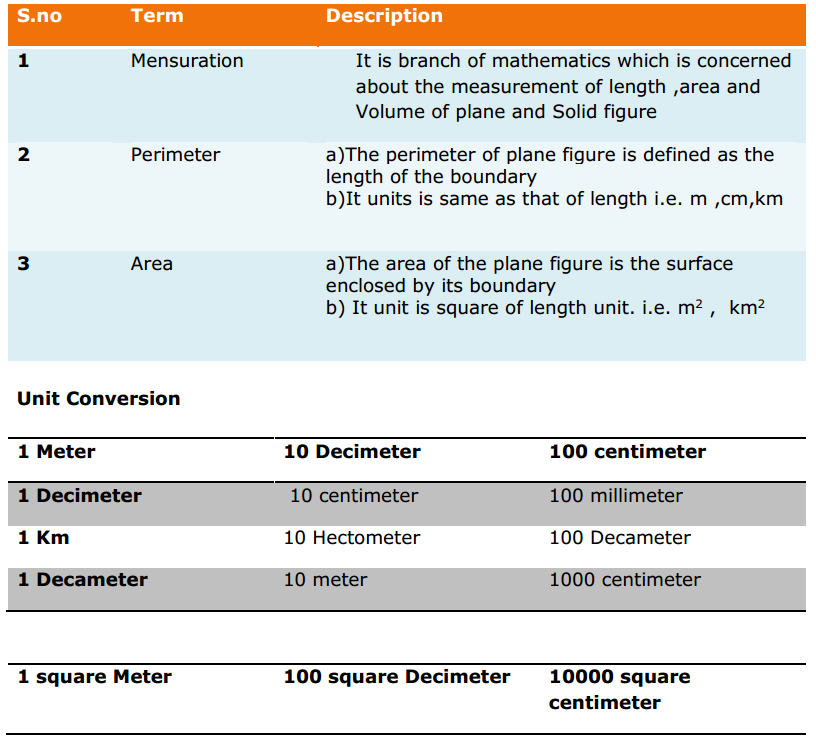
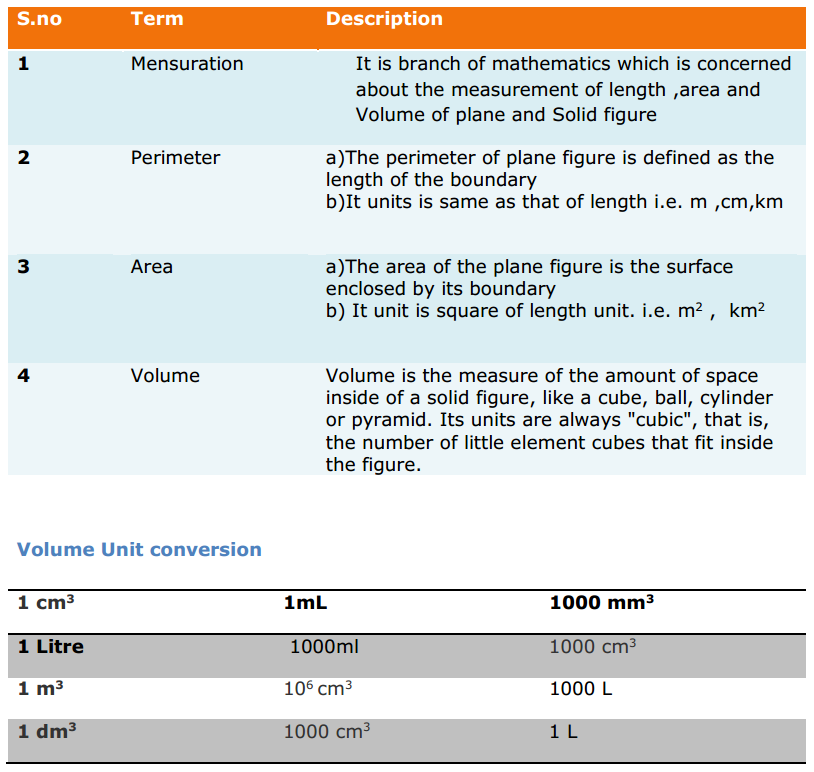
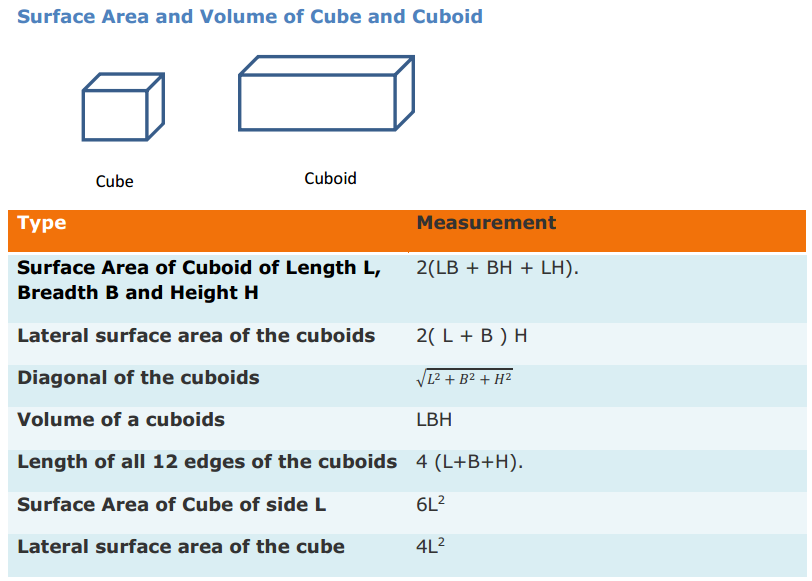
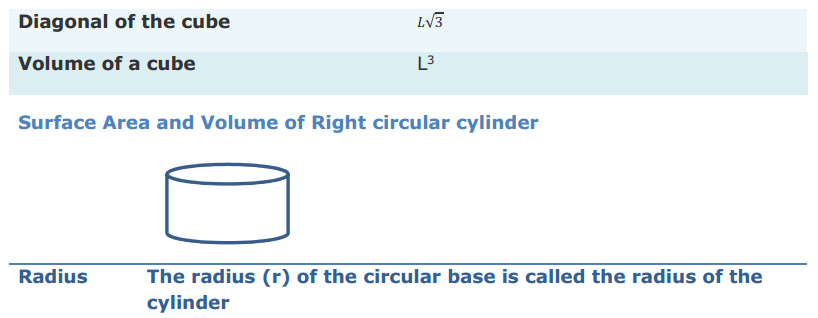
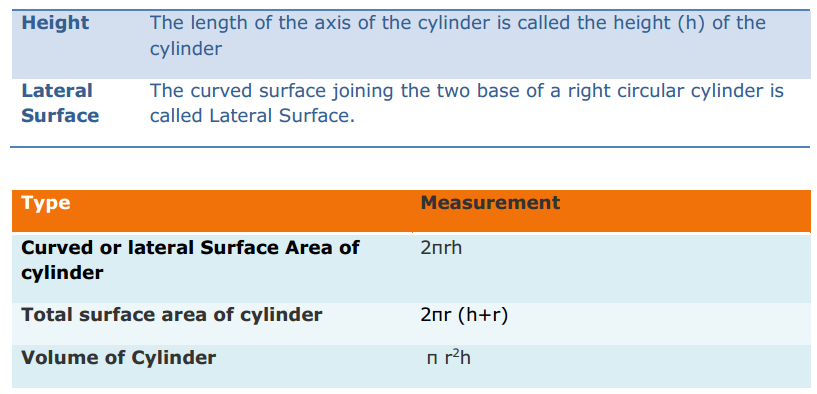
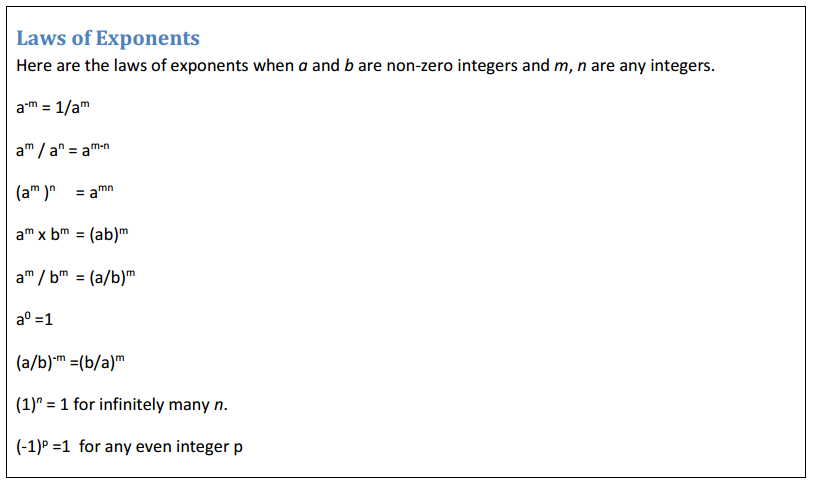
Most of the Students feel Maths as a Difficult Subject and Quite Hard to Master. To help all such people we have come up with Maths Formulas for Class 11. The only way to get grip on the subject is through consistent practice and learn the complete Math Formulae of Class 11. Do your best in the exam by accessing the Formulae List of 11th Std Maths and become familiar with concepts. Apply the formulas in your problems and arrive at the solution easily.
Chapterwise Class 11 Maths Formulas List
Get a strong grip on the concepts by making the most out of the 11th Grade Math Formula Collection over here. Try to implement the formulas during your calculations and get the desired scores. You can download the 11th Class Maths Formulas prepared by subject expertise and rely on them whenever you need them. Just tap on the below available links and you will get related formulas all in one place making your job much simple.
- Class 11 Sets Formulas
- Class 11 Relations and Functions Formulas
- Class 11 Trigonometric Functions Formulas
- Class 11 Complex Numbers and Quadratic Equations Formulas
- Class 11 Permutations and Combinations Formulas
- Class 11 Binomial Theorem Formulas
- Class 11 Sequence and Series Formulas
- Class 11 Straight Lines Formulas
- Class 11 Conic Sections Formulas
- Class 11 Introduction to Three Dimensional Geometry Formulas
- Class 11 Limits and Derivatives Formulas
- Class 11 Statistics Formulas
Coordinate Geometry & Line Formula
| Coordinate Geometry & Lines Formulas for Class 11 | |
|---|---|
| Distance Formula | \(\left | P_{1}P_{2} \right |=\sqrt{\left ( x_{2}-x_{1} \right )^{2}+\left ( y_{2}-y_{1} \right )^{2}}\) |
| Slope | \(\large m=\frac{rise}{run}=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) |
| Point-Slope Form | \(y-y_{1}=m\left ( x-x_{1} \right )\) |
| Point-Point Form | \(y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\left ( x-x_{1} \right )\) |
| Slope-Intercept Form | \(y=mx+b\) |
| Intercept-Intercept Form | \(\frac{x}{a}+\frac{y}{b}=1\) |
| General Form | \(Ax+By+C=0\) |
| Parallel & Perpendicular Lines | Parallel Lines \(m_{1}=m_{2}\) Perpendicular Lines \( m_{1}m_{2}=-1\) |
| Distance from a Point to a Line | \(\large d=\frac{\left | Ax_{0}+By_{0}+C \right |}{\sqrt{A^{2}+B^{2}}}\) |
Algebra Formula
| Algebra Formulas For Class 11 | |
|---|---|
| Distributive Property | \(a\times \left ( b+c \right ) = a \times b\, +\, a \times c\) |
| Commutative Property of Addition | \(a\, +\, b\, =\, b\, +\, a\) |
| Commutative Property of Multiplication | \(a\,\times b\, =\, b\,\times a\) |
| Associative Property of Addition | \(a\, +\, \left ( b\, +\, c \right ) = \left ( a\, +\, b \right )\, +\, c\) |
| Associative Property of Multiplication | \(a\,\times \left ( b\,\times c \right ) = \left ( a\,\times b \right )\,\times c\) |
| Additive Identity Property | \(a\, +\, 0\, =\, a\) |
| Multiplicative Identity Property | \(a\, \times 1\, =\, a\) |
| Additive Inverse Property | \(a\,+\left ( -a \right )=0\) |
| Multiplicative Inverse Property | \(a \cdot \left ( \frac{1}{a} \right )=1\) |
| Zero Property of Multiplication | \(a\times \left ( 0\right )=0\) |
Trigonometric Formula
| Trigonometry Class 11 Formulas |
|---|
| \(\sin (-\theta ) = -\sin \theta\) |
| \(\cos (-\theta ) = \cos \theta\) |
| \(\tan (-\theta ) = -\tan \theta\) |
| \( cosec (-\theta ) = -cosec \theta\) |
| \(\sec (-\theta ) = \sec \theta\) |
| \(\cot (-\theta ) = -\cot \theta\) |
| Product to Sum Formulas |
| \(\sin \, x \,\ sin \, y = \frac{1}{2}\left [ \cos\left ( x – y \right ) -\cos \left ( x+y \right ) \right ]\) |
| \(\cos\, x \, \cos\, y = \frac{1}{2}\left [ \cos \left ( x – y \right ) + \cos \left ( x+y \right ) \right ]\) |
| \(\sin\, x \, \cos\, y = \frac{1}{2}\left [ \sin\left ( x + y \right ) + \sin \left ( x-y \right ) \right ]\) |
| \( \cos\, x \, \sin\, y = \frac{1}{2}\left [ \sin\left ( x + y \right ) – \sin\left ( x-y \right ) \right ]\) |
| Sum to Product Formulas |
| \(\sin\, x + \sin \, y = 2\, \sin \left ( \frac{x+y}{2} \right ) \cos \left ( \frac{x-y}{2} \right )\) |
| \(\sin\, x -\sin\, y = 2\, \cos \left ( \frac{x+y}{2} \right ) \sin \left ( \frac{x-y}{2} \right )\) |
| \(\cos \, x + \cos \, y = 2 \, \cos \left ( \frac{x+y}{2} \right ) \cos\left ( \frac{x-y}{2} \right )\) |
| \(\cos\, x -\cos\, y = – 2 \, \sin \left ( \frac{x+y}{2} \right ) \sin \left ( \frac{x-y}{2} \right )\) |
Maths Formulas For Class 11: Sets
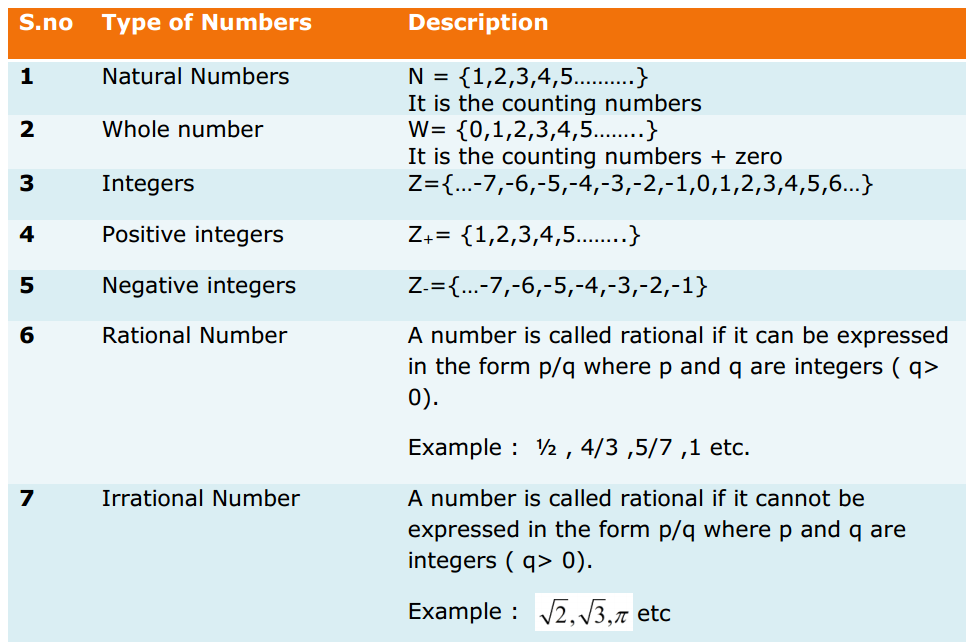
A set is a well-collaborated collection of objects. A set consisting of definite elements is a finite set. Otherwise, it is an infinite set. You can find the essential symbols and properties for Sets below:
| Symbol | Set |
| N | The set of all the natural numbers |
| Z | The set of all the integers |
| Q | The set of all the rational numbers |
| R | The set of all the real numbers |
| Z+ | The set of all the positive numbers |
| Q+ | The set of all the positive rational numbers |
| R+ | The set of all the positive real numbers |
- The union of two sets A and B are said to be contained elements that are either in set A and set B. The union of A and B is denoted as: \(A\cup B\).
- The intersection of two sets A and B are said to be contained elements that are common in both the sets. The intersection of A and B is denoted as: \(A\cap B\).
- The complement of a set A is the set of all elements given in the universal set U that are not contained in A. The complement of A is denoted as \({A}’\).
- For any two sets A and B, the following holds true:
- (i) \({(A\cup B)}’={A}’\cap{B}’\)
- (ii) \({(A\cap B)}’={A}’\cup{B}’\)
- If the finite sets A and B are given such that \({(A\cap B)}=\phi\), then: \(n{(A\cup B)}=n(A)+n(B)\)
- If \({(A\cup B)}=\phi\), then: \(n{(A\cup B)}=n(A)+n(B)-n(A\cap B)\)
Class 11 Maths Formulas: Relations And Functions
An ordered pair is a pair of elements grouped together in a certain order. A relation R towards a set A to a set B can be described as a subset of the cartesian product A × B which is obtained by describing a relationship between the first of its element x and the second of its element y given in the ordered pairs of A × B.
The below-mentioned properties will surely assist you in solving your Maths problems.
- A cartesian product A × B of two sets A and B is given by:
A × B = { \((a,b):a\epsilon A, b\epsilon B\) } - If (a , b) = (x , y); then a = x and b = y
- If n(A) = x and n(B) = y, then n(A × B) = xy
- A × \(\phi\) = \(\phi\)
- The cartesian product: A × B ≠ B × A
- A function f from the set A to the set B considers a specific relation type where every element x in the set A has one and only one image in the set B.
A function can be denoted as f: A → B, where f(x) = y - Algebra of functions: If the function f: X → R and g: X → R; we have:
- (i) \((f + g) (x) = f (x) + g(x), x\epsilon X\)
- (ii) \((f – g) (x) = f (x) – g(x), x\epsilon X\)
- (iii) \((f.g)(x) = f (x) .g (x), x\epsilon X\)
- (iv) \((kf) (x) = k ( f (x) ), x\epsilon X\), where k is a real number
- (v)\( \frac{f}{g}(x) = \frac{f(x)}{g(x)}, x\epsilon X, g(x)\neq 0\)
Maths Formulas For Class 11: Trigonometric Functions
In Mathematics, trigonometric functions are the real functions which relate to an angle of a right-angled triangle forming some finite ratios of two side lengths. Find the important Maths formulas for Class 11 related to trigonometric functions below.
- If in a circle of radius r, an arc of length l subtends an angle of θ radians, then \(l = r × θ\).
- Radian Measure = \(\frac{\pi}{180}\) × Degree Measure
- Degree Measure = \(\frac{180}{\pi}\) × Radian Measure
- \(cos^2 x + sin^2 x = 1\)
- \(1 + tan^2 x = sec^2 x\)
- \(1 + cot^2 x = cosec^2 x\)
- \(cos (2n\pi + x) = cos\: x\)
- \(sin (2n\pi + x) = sin\: x\)
- \(sin\: (-x) = -sin\: x\)
- \(cos\: (-x) = -cos\: x\)
- \(cos\:(\frac{\pi}{2}-x)=sin\:x\)
- \(sin\:(\frac{\pi}{2}-x)=cos\:x\)
- \(sin\: (x + y) = sin\: x\times cos\: y+cos\: x\times sin\: y\)
- \(cos\: (x + y) = cos\: x\times cos\: y-sin\: x\times sin\: y\)
- \(cos\: (x – y) = cos\: x\times cos\: y+sin\: x\times sin\: y\)
- \(sin\: (x – y) = sin\: x\times cos\: y-cos\: x\times sin\: y\)
- \(cos\:(\frac{\pi}{2}+x)=-sin\:x\)
- \(sin\:(\frac{\pi}{2}+x)=cos\:x\)
- \(cos\: (\pi-x) = -cos\: x\)
- \(sin\: (\pi-x) = sin\: x\)
- \(cos\: (\pi+x) = -cos\: x\)
- \(sin\: (\pi+x) = -sin\: x\)
- \(cos\: (2\pi-x) = cos\: x\)
- \(sin\: (2\pi-x) = -sin\: x\)
- If there are no angles x, y and (x ± y) is an odd multiple of (π / 2); then:
- (i) \(tan\:(x+y)=\frac{tan\:x+tan\:y}{1-tan\:x\:tan\:y}\)
- (ii) \(tan\:(x-y)=\frac{tan\:x-tan\:y}{1+tan\:x\:tan\:y}\)
- If there are no angles x, y and (x ± y) is an odd multiple of π; then:
- (i) \(cot\:(x+y)=\frac{cot\:x\:cot\:y-1}{cot\:y+cot\:x}\)
- (ii) \(cot\:(x-y)=\frac{cot\:x\:cot\:y+1}{cot\:y-cot\:x}\)
- \(cos\:2x=cos^2\:x-sin^2\:x=2\:cos^2\:x-1=1-2\:sin^2\:x=\frac{1-tan^2\:x}{1+tan^2\:x}\)
- \(sin\:2x=2\:sin\:x:cos\:x=\frac{2\:tan\:x}{1+tan^2\:x}\)
- \(sin\:3x=3\:sin\:x-4\:sin^3\:x\)
- \(cos\:3x=4\:cos^3\:x-3\:cos\:x\)
- \(tan\:3x=\frac{3\:tan\:x-tan^3\:x}{1-3\:tan^2\:x}\)
- Addition and Subtraction of sin and cos
- (i) \(cos\:x+cos\:y=2\:cos\frac{x+y}{2}\:cos\frac{x-y}{2}\)
- (ii) \(cos\:x-cos\:y=-2\:sin\frac{x+y}{2}\:sin\frac{x-y}{2}\)
- (iii) \(sin\:x+sin\:y=2\:sin\frac{x+y}{2}\:cos\frac{x-y}{2}\)
- (iv) \(sin\:x-sin\:y=2\:cos\frac{x+y}{2}\:sin\frac{x-y}{2}\)
- Multiplication of sin and cos
- (i) \(2\:cos\:x\:cos\:y=cos\:(x+y)+cos\:(x-y)\)
- (ii) \(-2\:sin\:x\:sin\:y=cos\:(x+y)-cos\:(x-y)\)
- (iii) \(2\:sin\:x\:cos\:y=sin\:(x+y)+sin\:(x-y)\)
- (iv) \(2\:cos\:x\:sin\:y=sin\:(x+y)-sin\:(x-y)\)
- \(sin\: x = 0;\: gives\: x = n\pi,\: where\: n\: \epsilon\: Z\)
- \(cos\: x = 0;\: gives\: x = (2n+1)\frac{\pi}{2},\: where\: n\: \epsilon\: Z\)
- \(sin\: x = sin\: y;\: implies\: x = n\pi\:+(-1)^n\:y,\: where\: n\: \epsilon\: Z\)
- \(cos\: x = cos\: y;\: implies\: x = 2n\pi\pm y,\: where\: n\: \epsilon\: Z\)
- \(tan\: x = tan\: y;\: implies\: x = n\pi+y,\: where\: n\: \epsilon\: Z\)
Class 11 Maths Formulas: Complex Numbers And Quadratic Equations
A number that can be expressed in the form a + ib is known as the complex number; where a and b are the real numbers and i is the imaginary part of the complex number.
- Let z1 = a + ib and z2 = c + id; then:
- (i) z1 + z2 = (a + c) + i (b + d)
- (ii) z1 . z2 = (ac – bd) – i (ad + bc)
- If there is a non-zero complex number; z = a + ib; where (a ≠ 0, b ≠ 0), then there exists a complex number \(\frac{a}{a^2+b^2}+i\frac{-b}{a^2+b^2}\); denoted by \(\frac{1}{z} or z–1 is known as the multiplicative inverse of z; such that
(a + ib) [ \(\frac{a^2}{a^2+b^2}+i\frac{-b}{a^2+b^2}\) ] = 1 + i 0 = 1 - For every integer k, i4k = 1, i4k+1 = i, i4k+2 = -1, i4k+3 = -i
- The conjugate of the complex number is \(\bar{z}=a-ib\)
- The polar form of the complex number z = x + iy is \(r(cos\: \theta+i\:sin\:\theta)\); where \(r=\sqrt{x^2+y^2}\) (the modulus of z)
\(cos\:\theta =\frac{x}{r}\) and \(sin\:\theta =\frac{y}{r}\) (θ is the argument of z) - A polynomial equation with n degree has n roots.
- The solutions of the quadration equation ax2 + bx + c = 0 are:
\(x=\frac{-b\pm \sqrt{4ac-b^2i}}{2a}\) where a, b, c ∈ R, a ≠ 0, b2 – 4ac < 0
Maths Formulas For Class 11: Permutations And Combinations
If a certain event occurs in ‘m’ different ways followed by an event that occurs in ‘n’ different ways, then the total number of occurrence of the events can be given in m × n order. Find the important Maths formulas for class 11 as under:
- The number of permutations of n different things taken r at a time is given by \({}^{n}\textrm{P}{r}\) \(=\frac{n!}{(n-r)!}\) where 0 ≤ r ≤ n
- \(n!=1\times 2\times 3\times …\times n\)
- \(n!=n\times (n-1)!\)
- The number of permutations of n different things taken r at a time with repetition being allowed is given as: nr
- The number of permutations of n objects taken all at a time, where p1 objects are of one kind, p2 objects of the second kind, …., pk objects of kth kind are given as: \(\frac{n!}{p_{1}!\:p_{2}!\:…\:p_{k}!}\)
- The number of permutations of n different things taken r at a time is given by \({}^{n}\textrm{C}{r}\) \(=\frac{n!}{r!(n-r)!}\) where 0 ≤ r ≤ n
Class 11 Maths Formulas: Binomial Theorem
A Binomial Theorem helps to expand a binomial given for any positive integral n.
\((a+b)^n={}^{n}\textrm{C}_{0}\:a^n+{}^{n}\textrm{C}_{1}\:a^{n-1}.b+{}^{n}\textrm{C}_{2}\:a^{n-2}.b^2+…+{}^{n}\textrm{C}_{n-1}\:a.b^{n-1}+{}^{n}\textrm{C}_{n}\:b^n\)
- The general term of an expansion (a + b)n is \(T_{r+1}={}^{n}\textrm{C}_{r}\:a^{n-r}.b^r\)
- In the expansion of (a + b)n; if n is even, then the middle term is \((\frac{n}{2}+1)^{th}\) term.
- In the expansion of (a + b)n; if n is odd, then the middle terms are \((\frac{n+1}{2})^{th}\) and \((\frac{n+1}{2}+1)^{th}\) terms
Maths Formulas For Class 11: Sequence And Series
An arithmetic progression (A.P.) is a sequence where the terms either increase or decrease regularly by the same constant. This constant is called the common difference (d). The first term is denoted by a and the last term of an AP is denoted by l.
- The general term of an AP is \(a_{n}=a+(n-1)\:d\)
- The sum of the first n terms of an AP is: \(S_{n}=\frac{n}{2}[2a+(n-1)\:d]=\frac{n}{2}(a+l)\)
A sequence is said to be following the rules of geometric progression or G.P. if the ratio of any term to its preceding term is specifically constant all the time. This constant factor is called the common ratio and is denoted by r.
- The general term of an GP is given by: \(a_{n}=a.r^{n-1}\)
- The sum of the first n terms of a GP is: S_{n}=\frac{a(r^n-1)}{r-1}\: or\: \frac{a(1-r^n)}{1-r}; if r ≠ 1
- The geometric mean (G.M.) of any two positive numbers a and b is given by \(\sqrt{ab}\)
Class 11 Maths Formulas: Straight Lines
- Slope (m) of the intersecting lines through the points (x1, y1) and x2, y2) is given by \(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\); where x1 ≠ x2
- An acute angle θ between lines L1 and L2 with slopes m1 and m2 is given by \(tan\:\theta =\left | \frac{m_{2}-m_{1}}{1+m_{1}.m_{2}} \right |\); 1 + m1.m2 ≠ 0.
- Equation of the line passing through the points (x1, y1) and (x2, y2) is given by: \(y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})\)
- Equation of the line making a and b intercepts on the x- and y-axis respectively is: \(\frac{x}{a}+\frac{y}{b}=1\)
- The perpendicular distance d of a line Ax + By + C = 0 from a point (x1, y1) is: \(d=\frac{\left | Ax_{1}+By_{1}+C \right |}{\sqrt{A^2+B^2}}\)
- The distance between the two parallel lines Ax + By + C1 and Ax + By + C2 is given by: d=\(\frac{\left | C_{1}-C_{2} \right |}{\sqrt{A^2+B^2}}\)
Maths Formulas For Class 11: Conic Sections
A circle is a geometrical figure where all the points in a plane are located equidistant from the fixed point on a given plane.
- The equation of the circle with the centre point (h, k) and radius r is given by (x – h)2 + (y – k)2 = r2
- The equation of the parabola having focus at (a, 0) where a > 0 and directrix x = – a is given by: y2 = 4ax
- The equation of an ellipse with foci on the x-axis is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
- Length of the latus rectum of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is given by: \(\frac{2b^2}{a}\)
- The equation of a hyperbola with foci on the x-axis is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
- Length of the latus rectum of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is given by: \(\frac{2b^2}{a}\)
Class 11 Maths Formulas: Introduction To Three Dimensional Geometry
The three planes determined by the pair of axes are known as coordinate planes with XY, YZ and ZX planes. Find the important Maths formulas for Class 11 below:
- The distance of two points P(x1, y1, z1) and Q(x2, y2, z2) is:
\(PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}\) - The coordinates of a point R that divides the line segment joined by two points P(x1, y1, z1) and Q(x2, y2, z2) internally as well as externally in the ratio m : n is given by:
\(\left ( \frac{mx_2+nx_1}{m+n},\frac{my_2+ny_1}{m+n},\frac{mz_2+nz_1}{m+n} \right )\:and\:\left ( \frac{mx_2-nx_1}{m-n},\frac{my_2-ny_1}{m-n},\frac{mz_2-nz_1}{m-n} \right )\); - The coordinates of the mid-point of a given line segment joined by two points P(x1, y1, z1) and Q(x2, y2, z2) are \(\left ( \frac{x_1+x_2}{2},\frac{y_1+y_2}{2},\frac{z_1+z_2}{2} \right )\)
- The coordinates of the centroid of a given triangle with vertices (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) are \(\left ( \frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3},\frac{z_1+z_2+z_3}{3} \right )\)
Maths Formulas For Class 11: Limits And Derivatives
A limit of a function at a certain point holds a common value of the left as well as the right hand limits, if they coincide with each other.
- For functions f and g, the following property holds true:
- (i) \(\lim\limits_{x \to a} \left [ f(x)\pm g(x) \right ]= \lim\limits_{x \to a}f(x) \pm \lim\limits_{x \to a}g(x)\)
- (ii) \(\lim\limits_{x \to a} \left [ f(x) .g(x) \right ]= \lim\limits_{x \to a}f(x) . \lim\limits_{x \to a}g(x)\)
- (iii) \(\large \lim\limits_{x \to a} \left [ \frac{f(x)}{g(x)} \right ] = \frac{\lim\limits_{x \to a}f(x)}{\lim\limits_{x \to a}g(x)}\)
- Standard Limits
- (i) \(\lim\limits_{x \to a}\frac{x^n-a^n}{x-a}= n\:a^{n-1}\)
- (ii) \(\lim\limits_{x \to a}\frac{sin\:x}{x}=1\)
- (iii) \(\lim\limits_{x \to a}\frac{1-cos\:x}{x}=0\)
- The derivative of a function f at a holds as: \({f}'(a)=\lim\limits_{x \to a}\frac{f(a+h)-f(a)}{h}\)
- The derivative of a function f at a given point x holds as: \({f}'(x)=\frac{\partial f(x)}{\partial x}=\lim\limits_{x \to a}\frac{f(x+h)-f(x)}{h}\)
- For the functions u and v, the following holds true:
- (i) \((u\pm v)’=u’\pm v’\)
- (ii) \((uv)’=u’v+uv’\)
- (iii) \(\left ( \frac{u}{v} \right )’=\frac{u’v-uv’}{v^2}\)
- Standard Derivatives
- (i) \(\frac{\partial}{\partial x}(x^n)=nx^{n-1}\)
- (ii) \(\frac{\partial}{\partial x}(sin\:x)=cos\:x\)
- (iii) \(\frac{\partial}{\partial x}(cos\:x)=-sin\:x\)
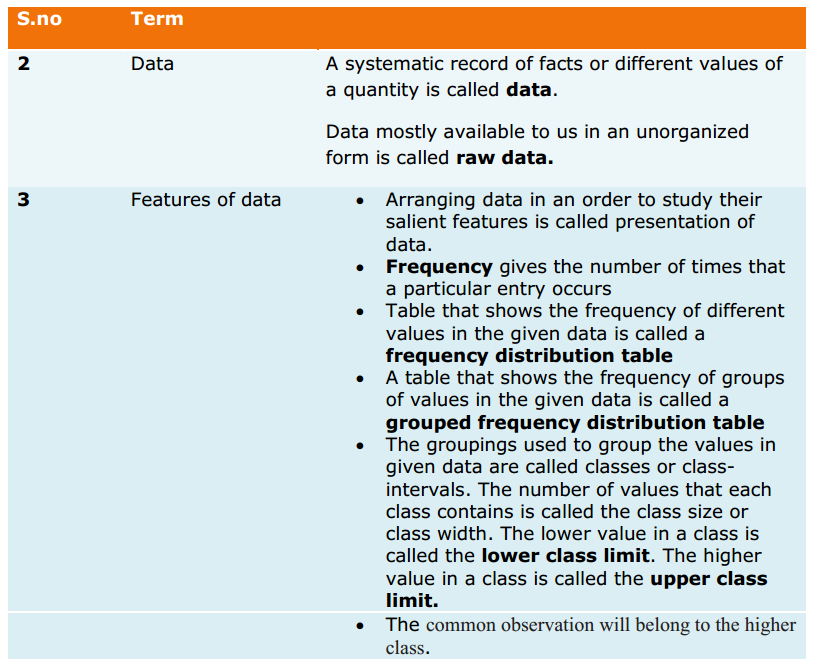
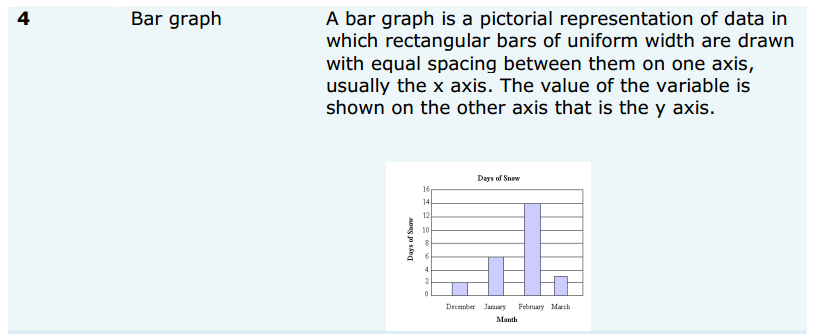
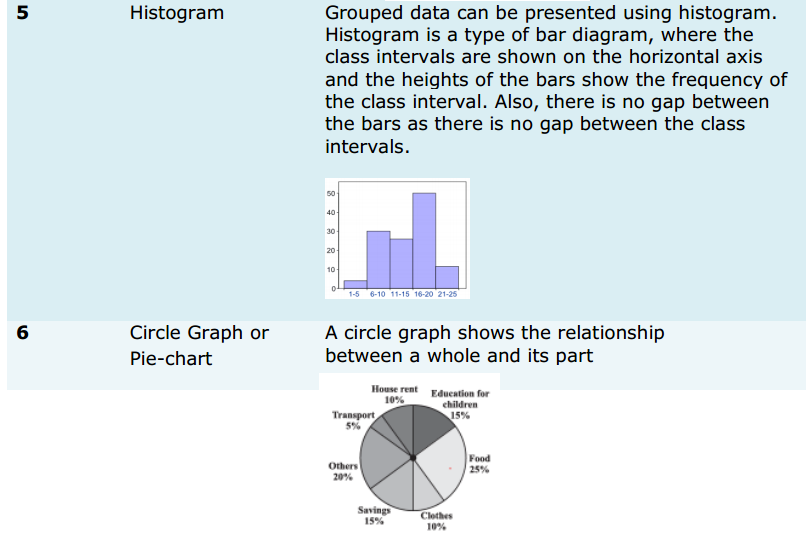
Class 11 Maths Formulas: Statistics
You will find the essential maths formulas for Class 11 of Statistics given below:
- Mean Deviation for the ungrouped data:
- (i) \(M.D.(\bar x)=\frac{\sum \left | x_i-\bar x \right |}{n}\)
- (ii) \(M.D.(M)=\frac{\sum \left | x_i-M \right |}{n}\)
- Mean Deviation for the grouped data:
- (i) \(M.D.(\bar x)=\frac{\sum f_i|x_i-\bar x|}{N}\)
- (ii) \(M.D.(M)=\frac{\sum f_i|x_i-M|}{N}\)
- Variance and Standard Deviation for the ungrouped data:
- (i) \(\sigma ^2=\frac{1}{N}\sum (x_i-\bar x)^2\)
- (ii) \(\sigma=\sqrt{\frac{1}{N}\sum (x_i-\bar x)^2}\)
- Variance and Standard Deviation of a frequency distribution (discrete):
- (i) \(\sigma ^2=\frac{1}{N}\sum f_i(x_i-\bar x)^2\)
- (ii) \(\sigma=\sqrt{\frac{1}{N}\sum f_i(x_i-\bar x)^2}\)
- Variance and Standard Deviation of a frequency distribution (continuous):
- (i) \(\sigma ^2=\frac{1}{N}\sum f_i(x_i-\bar x)^2\)
- (ii) \(\sigma=\frac{1}{N}\sqrt{N\sum f_ix_i^2-(\sum f_ix_i)^2}\)
- Coefficient of variation (C.V.) = \(\frac{\sigma}{\bar x}\times 100\) ; where \(\bar x\neq 0\)