Shapes of Orbitals of an Atom
What is orbital?
In chemistry, an orbital is a mathematical function which portrays the wave-like behavior of an electron pair, electron or nucleons in Quantum Mechanics and Chemistry. Orbitals are also referred to as electron or atomic orbitals.
Atomic orbitals are the three- dimensional regions of space around the nucleus of an atom. Atomic orbitals allow the atoms to make covalent bonds. s, p, d and f orbitals are the most commonly filled orbitals. As defined by the Pauli Exclusion Principle, only two electrons can be found in any orbital space.
All the electrons which have the same value for n i.e the principal quantum number will be in the same shell. When the electrons share the same n, l and m they are said to be in the same orbital i.e. they have the same energy level, and they differ only in spin quantum number.
Nodes:
Node is a region where the probability of finding the electron will be zero. The nodal plane is the plane that passes through the nucleus on which the probability of finding an electron is zero. In an orbital, the number of nodal planes is equal to the azimuthal quantum number.
There are two types of nodes, they are angular and radial nodes. Angular nodes will be typically flat at fixed angles. Radial nodes are spheres at a fixed radius which occurs as the principal quantum number increases.

The total number of nodes of an orbital is the sum of angular and radial nodes and it is given in the terms of n and l quantum number and is given below:
N = n – l – 1
Types of Orbitals and their shapes:
Atomic Orbitals can be classified into many types like s, p, d, f, g, h etc. But only the first four of the mentioned orbitals will be occupied on the ground state of an atom. Following are the explanation for the orbitals and their shapes:
The total values permitted form for a given value of I gives the number of orbitals of a type within a subshell. The four types of atomic orbitals match up to the values of l= 0, 1, 2 and 3. The orbitals with the value l = 0 are the s orbitals and they are spherically symmetrical in shape. It is with the greatest probability of finding the electron occurring at the nucleus.
The orbitals with the value l= 1 are the p orbitals which contain a nodal plane including the nucleus hence forming a dumbbell shape.
The orbitals with l= 2 are the d orbitals which have complex shapes with at least two nodal surfaces. The orbitals with l= 3 are called the f orbitals that are more complex.
Since the average distance from the nucleus will determine the energy of an electron, each atomic orbital with a given set of quantum numbers will have particular energy associated with it, which is called as the orbital energy.
E = Z2/ n2 Rhc
The distribution of orbitals into their inner electronic core is called as the penetration of orbitals. Example: The 2s orbital’s radial density is spread into the curve of 1s orbital. Same way, 3s orbital will be spread into 1s orbital and 2s orbital. Due to the spreading of electrons in 2s or 3s orbitals, it will not be screened fully by the inner 1s electrons from the nucleus. From s
orbitals to f orbitals, the extent of penetration decreases.
s > p > d > f
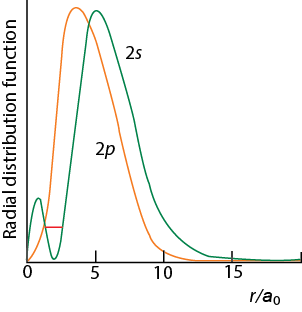
The above diagram denotes the penetration decrease from s to p orbitals as the radial distribution close to nucleus for s is more when compared to p orbitals.
An ion or atom with one or more electrons occupies the higher energy orbitals and it is said to be in an excited state, whereas an ion or atom in which one or more electrons occupy low energy orbitals is said to be in its ground state.
The shape of Orbitals:
A large number of orbitals occupy an atom. If an orbital is smaller in size means that there is more possibility of finding the electron near to the nucleus. Same way, for the shape there is more possibility for finding electron along certain directions rather than with the others.
The shape of 1s orbital:
The value of quantum numbers l and m are 0 for the s orbitals. The functions of Φ and Θ are independent of angles Φ and Θ for these values.

Each of the above mentioned two functions is equal to a constant term and for such orbitals, the equation will be
Ψ2n, 0, 0 α R2n, 0
Angular function of s orbitals: ΘΦ = (1/4π)½
For s orbitals, l = 0, the angular wave function is independent and constant of the angles Φ and θ. A2 is the probability of finding an electron at a specified direction Φ and Θ from nucleus to infinity at any distance.
For s orbital, the probability of finding the electron is maximum at r= 0 and it decreases exponentially with a distance r. the plots of R and R^2 are spherically symmetrical around the nucleus, so these plots exist around the nucleus.

The three- dimensional plots of ψ^2 Vs r is clear from the above diagram of the dot- population picture or boundary surface. In the above dot- population picture, the relative probability value at a given location is shown by the density dots near to it.
The dot population picture shows the actual description of the time average distribution of the electron. In the above diagram, the dot population picture R 2/ 1s Vs r is shown clearly.
In the equal probability contours, the contours can be drawn by joining the points of identical probability. For any of the s orbital, around the nucleus, these contours are spherically symmetrical.
The shape of 2s orbital:
For 2s orbital, it will be
Ψ 2/ 2, 0, 0 α R 2/ 2, 0
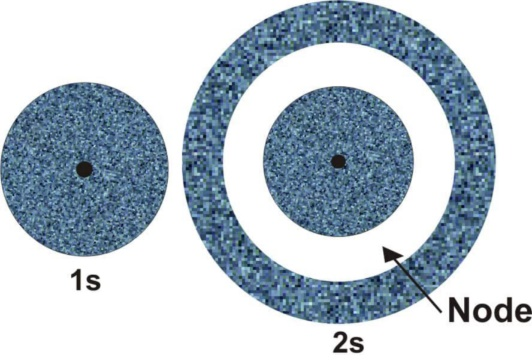
The dot population picture for 2s orbital which is shown above.
For the given value of r, the function of R might have positive value, zero or even negative value. The probability plots will always be positive as the square of a negative quantity or positive quantity is always positive.
From the above diagram, it is clear that for 2s orbital, there will be 2 maxima in the R 2/ 2 Vs r plot. It will be one at r= 0 and the other one at nearly 2= 210 pm, between these two maxima the probability becomes zero at about r= 105 pm. this is called as the nodal point.
The size of the 2s orbital is larger than that of the 1s orbital. This is because the 2s orbital size resides farther away from the nucleus when compared to that of the 1s orbital.
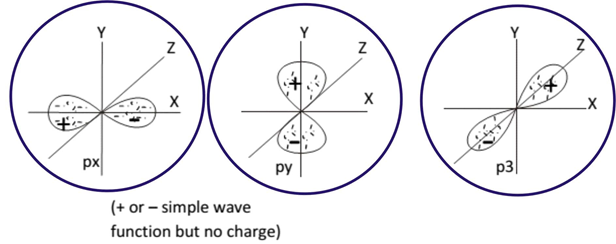
The shape of p orbital:
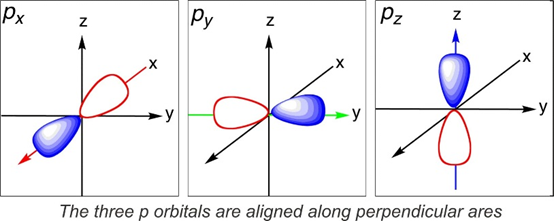
Here, the quantum number m fixes the angular momentum direction. The quantum number also fixes the direction of the orbital in the space.
Example: There are three orbitals of p orbitals (I= 1)
These values correspond to the three values of m(+1, 0, -1). The P0, P+1 + P-1 and P+1 – P-1 plots indicates the dumb-bell shaped orbitals. These are also perpendicular to each other pointing towards the x, y, and z-axis. For this reason, they are called as px, py, pz orbitals.
The shape of 2p orbitals:
I= 1 for the p orbitals and there will be three orbitals for this type. These orbitals will correspond to three different values which are =1, 0, -1 of the magnetic quantum number called m.
Ψ^2 2, 1, 0 = R 2/ 2 θ^2 1, 0 Φ 2/ 0
Ψ^2 /2, 1+ 1 = R 2/ 2, 1 θ^2/ 1, 1 Φ 2/ 1
Ψ^2 /2, 1, -1 = R 2/ 2, 1 θ^2/ 1, 1 Φ 2/ -1
For all the three 2p orbitals, the R2, 1 Vs r and R2/ 2 Vs r plots are same. This because the function of R depends only on the quantum numbers I and n.
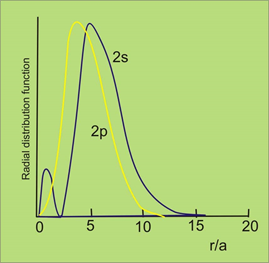
Unlike the 2s orbital, the 2p orbital the probability will be minimum at the nucleus and it has a maximum value of r= 104 pm. thereby, with the distance it decreases exponentially. The 2p orbitals will have directional characteristics which are due to the angular functions Φ and ʘ.
The shape of d orbital:
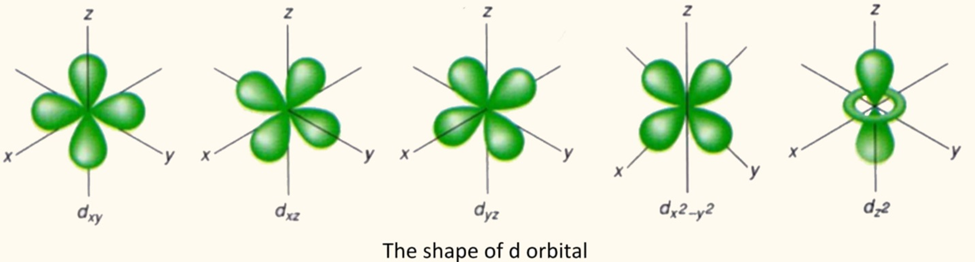
There are five d orbitals which are selected as “dx y, d y z, dx z”, dx^2-y^2, dz^2. The energy of the d orbitals are equivalent but the shape of dz^2 orbitals is different from the other ones.
The shape of 3d orbitals:
The value of I= 2 for d orbitals and for I= 2 the five values of m are permissible. The values for the d type orbitals are +2, +1, 0, -1 and -2.
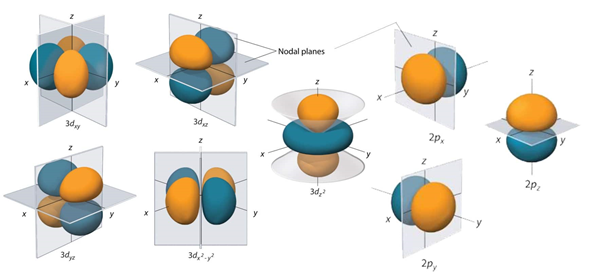
It is necessary to have the knowledge of the 3 d orbitals as it will be helpful in discussing the chemistry of many elements.the 3d orbitals can be classified into 2 categories. They are as follows:
1. Orbitals that has maximum probability distribution along with the 3dz^2 and 3d x^2-y^2 axes and
2. Orbitals that has a maximum probability distribution in between the two axes 3dxy, 3dyz and 3dxz.
f orbital:
An f orbital has the secondary quantum number l = 3. There are seven f orbitals with ml = -3, -2, -1, 0, +1, +2, +3 and these orbitals are not occupied in the ground state until element 58 (cerium). [Xe] 6s²4f5d is the electronic configuration for cerium.
The f orbitals are deeply buried beneath the valence shell even for the elements beyond cerium. f orbitals have three nodal planes and it has complex shapes with the atomic nucleus at the center.

The 4y3-3x2y orbital match up to l = 3, ml = -3, and n = 4.
The 4fxyz orbital match up to l = 3, ml = -2, and n = 4.
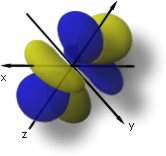
The 4f5yz2-yr2 orbital match up to l = 3, ml = -1, and n = 4.

The 4f5z3-3zr2 orbital match up to l = 3, ml = 0, and n = 4.
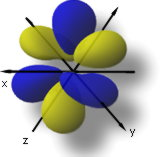
The 4f5xz2-xr2 orbital match up to l = 3, ml = +1, and n = 4.
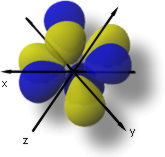
The 4fzx3-xy2 orbital match up to l = 3, ml = +2, and n = 4.
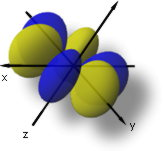
The 4fx3-3xy2 orbital match up to l = 3, ml = +3, and n = 4.