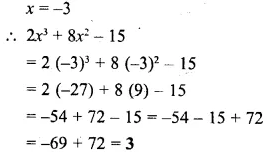Selina Concise Mathematics Class 6 ICSE Solutions Chapter 20 Substitution (Including Use of Brackets as Grouping Symbols)
Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 20 Substitution (Including Use of
Brackets as Grouping Symbols)
Substitution Exercise 20A – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Fill in the following blanks, when :
x = 3,y = 6, z = 18, a = 2, b = 8, c = 32 and d = 0.
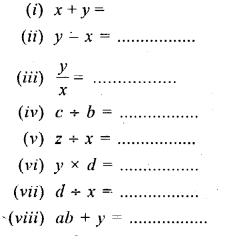
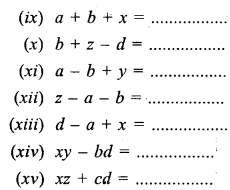
Solution:
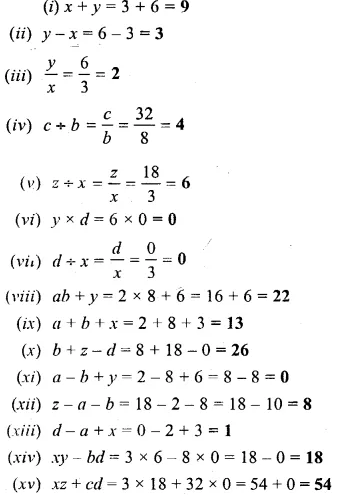
Question 2.
Find the value of :
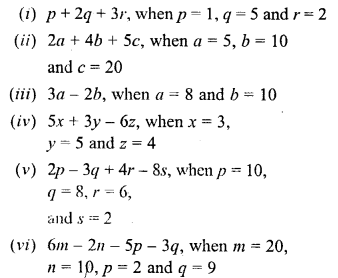
Solution:
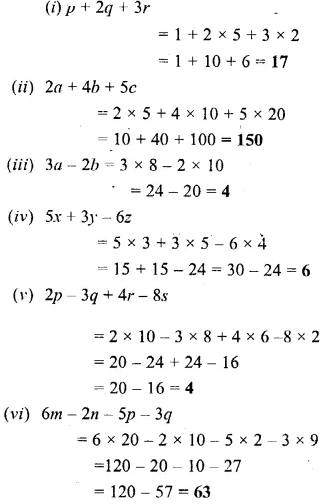
Question 3.
Find the value of :
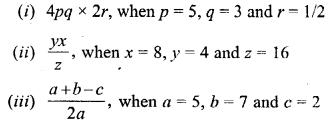
Solution:
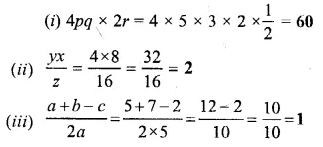
Question 4.
If a = 3, b = 0, c = 2 and d = 1, find the value of :
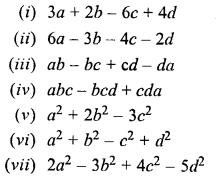
Solution:
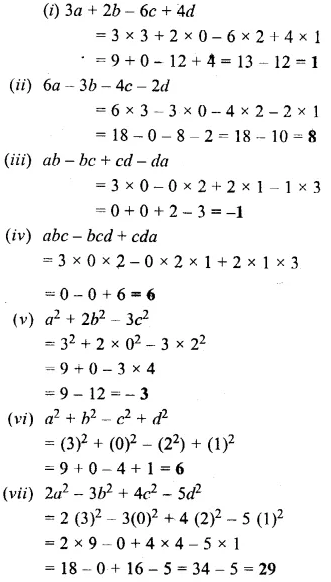
Question 5.
Find the value of 5x2 – 3x + 2, when x = 2.
Solution:
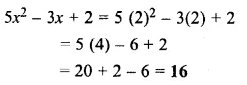
Question 6.
Find the value of 3x3 – 4x2 + 5x – 6, when x = -1.
Solution:
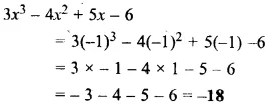
Question 7.
Show that the value of x3 – 8x2 + 12x – 5 is zero, when x = 1.
Solution:
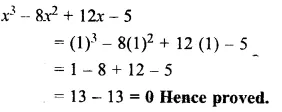
Question 8.
State true and false :
(i) The value of x + 5 = 6, when x = 1
(ii) The value of 2x – 3 = 1, when x = 0
(iii) \(\frac { 2x-4 }{ x+1 }\) = -1,when x = 1
Solution:
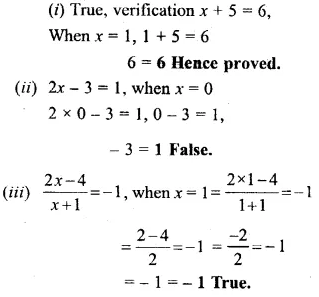
Question 9.
If x = 2, y = 5 and z = 4, find the value of each of the following :
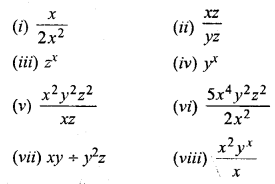
Solution:
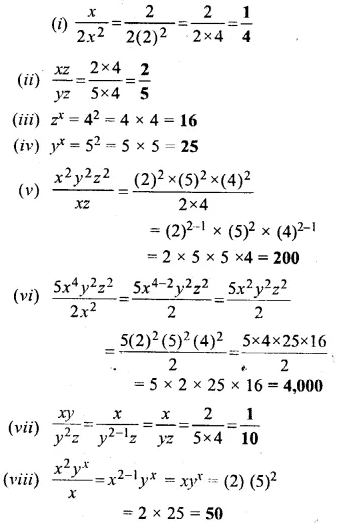
Question 10.
If a = 3, find the values of a2 and 2a.
Solution:
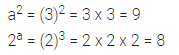
Question 11.
If m = 2, find the difference between the values of 4m3 and 3m4.
Solution:
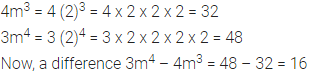
Substitution Exercise 20B – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Evaluate :
(i) (23 – 15) + 4
(ii) 5x + (3x + 7x)
(iii) 6m – (4m – m)
(iv) (9a – 3a) + 4a
(v) 35b – (16b + 9b)
(vi) (3y + 8y) – 5y
Solution:
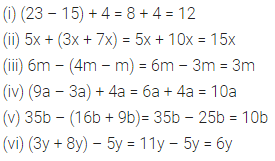
Question 2.
Simplify :
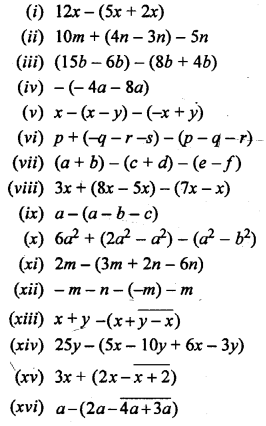
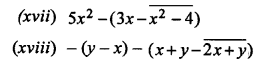
Solution:
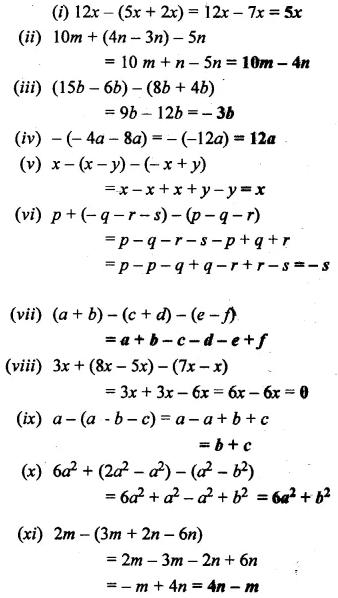
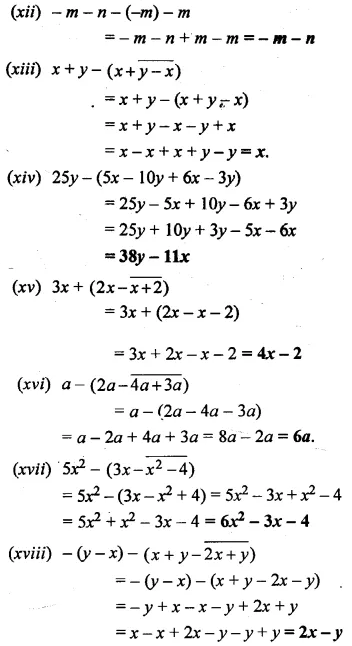
Question 3.
Simplify :
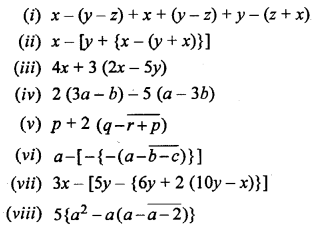
Solution:
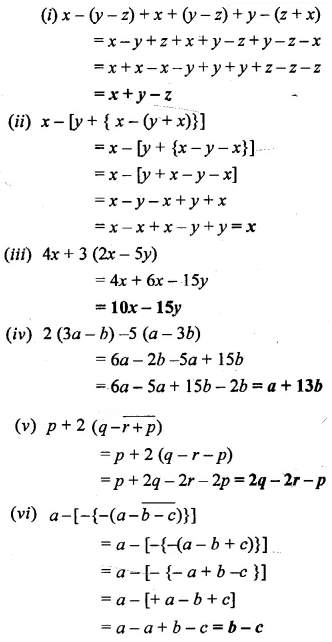
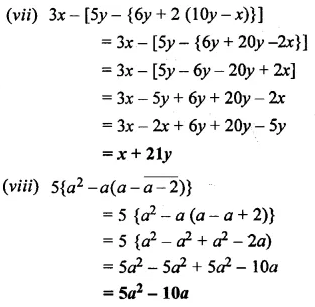
Substitution Exercise 20C – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Fill in the blanks :
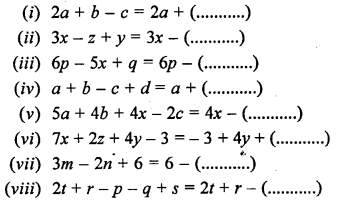
Solution:
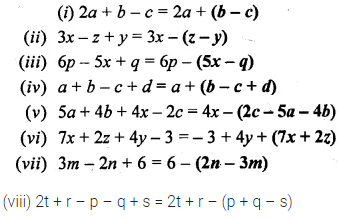
Question 2.
Insert the bracket as indicated :
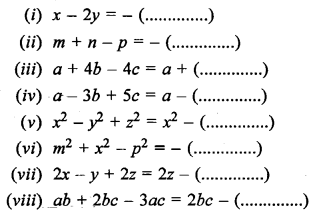
Solution:
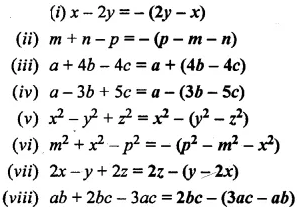
Substitution Revision Exercise – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Find the value of 3ab + 10bc – 2abc when a = 2, b = 5 and c = 8.
Solution:
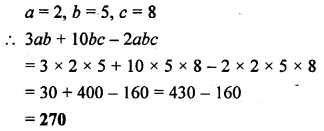
Question 2.
If x = 2, y = 3 and z = 4, find the value of 3x2 – 4y2 + 2z2.
Solution:
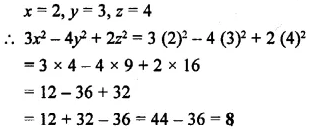
Question 3.
If x = 3, y = 2 and z = 1; find the value of:
(i) xy
(ii) yx
(iii) 3x2 – 5y2
(iv) 2x – 3y + 4z + 5
(v) y2 – x2 + 6z2
(vi) xy + y2z – 4zx
Solution:
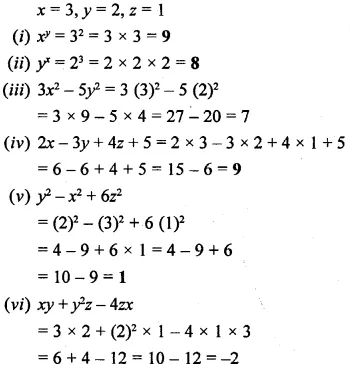
Question 4.
If P = -12x2 – 10xy + 5y2, Q = 7x2 + 6xy + 2y2, and R = 5x2 + 2xy + 4y2 ; find :
(i) P – Q
(ii) Q + P
(iii) P – Q + R
(iv) P + Q + R
Solution:
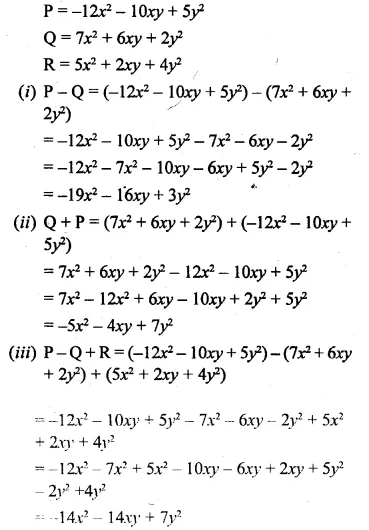
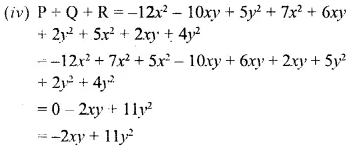
Question 5.
If x = a2 – bc, y = b2 – ca and z = c2 – ab ; find the value of :
(i) ax + by + cz
(ii) ay – bx + cz
Solution:
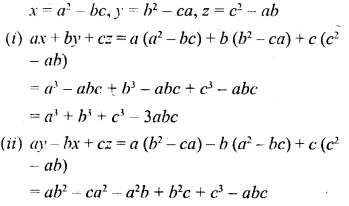
Question 6.
Multiply and then evaluate :
(i) (4x + y) and (x – 2y); when x = 2 and y = 1.
(ii) (x2 – y) and (xy – y2); when x = 1 and y = 2.
(iii) (x – 2y + z) and (x – 3z); when x = -2, y = -1 and z = 1.
Solution:
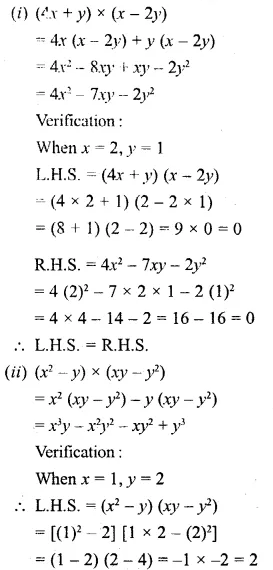

Question 7.
Simplify :
(i) 5 (x + 3y) – 2 (3x – 4y)
(ii) 3x – 8 (5x – 10)
(iii) 6 {3x – 8 (5x – 10)}
(iv) 3x – 6 {3x – 8 (5x – 10)}
(v) 2 (3x2 – 4x – 8) – (3 – 5x – 2x2)
(vi) 8x – (3x – \(\bar { 2x-3 }\))
(vii) 12x2 – (7x – \(\bar { 3x^{ 2 }+15 }\))
Solution:
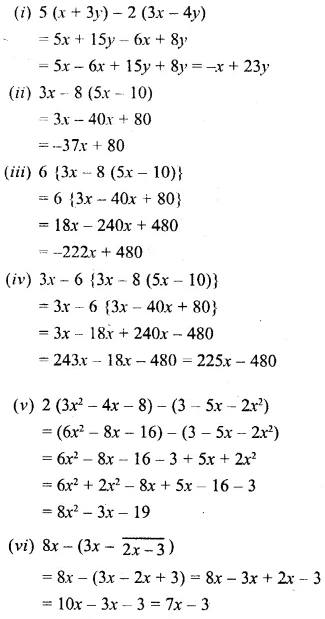
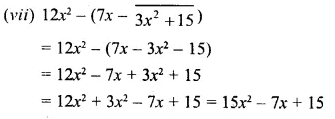
Question 8.
If x = -3, find the value of : 2x3 + 8x2 – 15.
Solution: