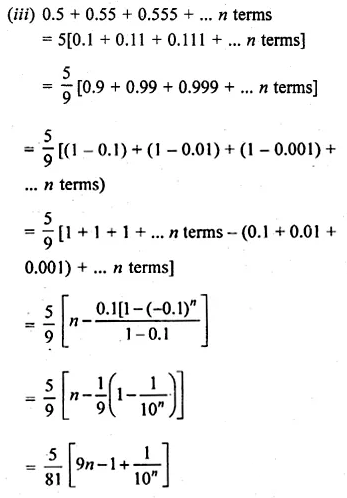ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
Question 1.
Find the sum of:
(i) 20 terms of the series 2 + 6 + 18 + …
(ii) 10 terms of series 1 + √3 + 3 + …
(iii) 6 terms of the GP. 1, \(– \frac { 2 }{ 3 } \) , \(\\ \frac { 4 }{ 9 } \), …
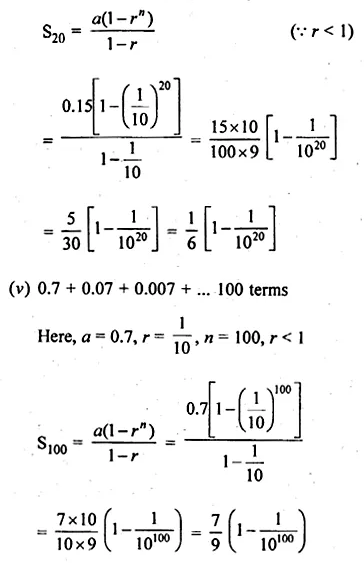
(iv) 20 terms of the GP. 0.15, 0.015, 0.0015,…
(v) 100 terms of the series 0.7 + 0.07 + 0.007 +…
(vi) 5 terms and n terms of the series \(1+\frac { 2 }{ 3 } +\frac { 4 }{ 9 } +…\)
(vii) n terms of the G.P. √7, √21, 3√7, …
(viii)n terms of the G.P. 1, -a, a², -a³, … (a ≠ -1)
(ix) n terms of the G.P. x3, x5 , x7, … (x ≠ ±1).
Solution:

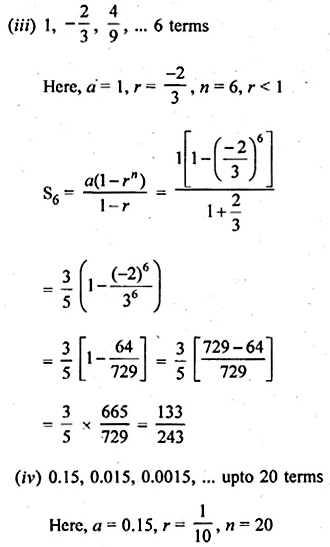
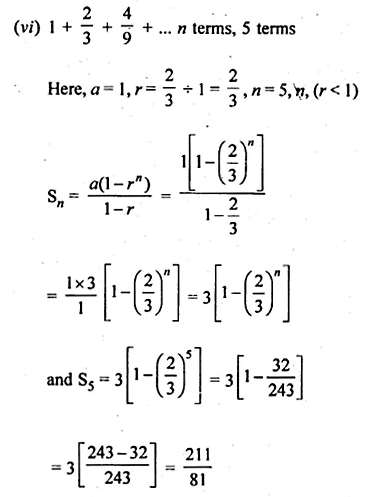

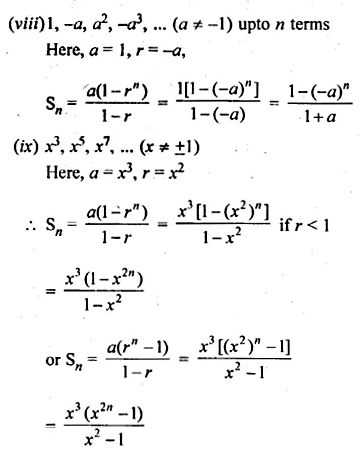
Question 2.
Find the sum of the first 10 terms of the geometric series
√2 + √6 + √18 + ….
Solution:

Question 3.
Find the sum of the series 81 – 27 + 9….\(– \frac { 1 }{ 27 } \)
Solution:
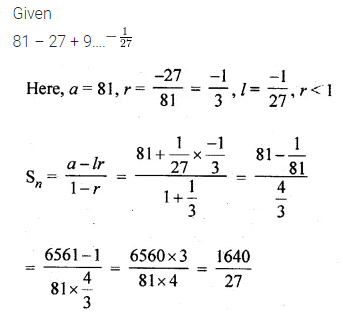
Question 4.
The nth term of a G.P. is 128 and the sum of its n terms is 255. If its common ratio is 2, then find its first term.
Solution:

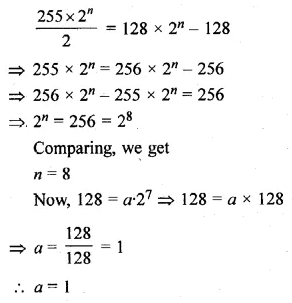
Question 5.
If the sum of the first six terms of any G.P. is equal to 9 times the sum of the first three terms, then find the common ratio of the G.P.
Solution:

Question 6.
A G.P. consists of an even number of terms. If the sum of all the terms is 3 times the sum of the odd terms, then find its common ratio.
Solution:

Question 7.
(i) How many terms of the G.P. 3, 32, 33, … are needed to give the sum 120?
(ii) How many terms of the G.P. 1, 4, 16, … must be taken to have their sum equal to 341?
Solution:

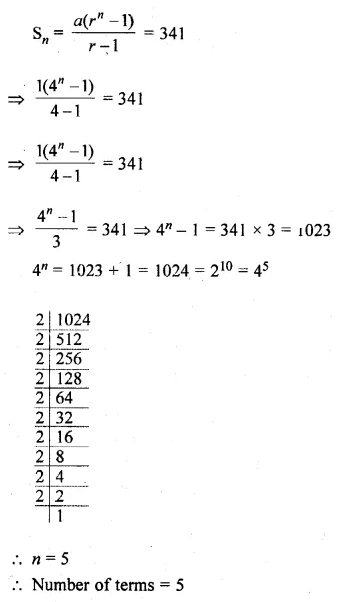
Question 8.
How many terms of the GP. 1, √2 > 2, 2 √2,… are required to give a sum of 1023( √2 + 1)?
Solution:


Question 9.
How many terms of the \(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } +…\) will make the sum \(\\ \frac { 55 }{ 72 } \) ?
Solution:
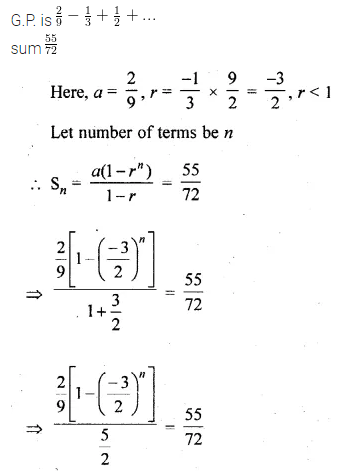
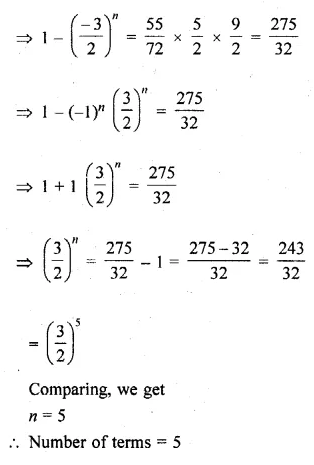
Question 10.
The 2nd and 5th terms of a geometric series are \(– \frac { 1 }{ 2 } \) and sum \(\\ \frac { 1 }{ 16 } \) respectively. Find the sum of the series upto 8 terms.
Solution:
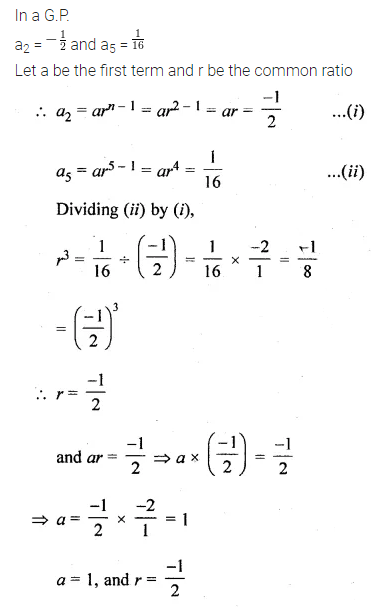
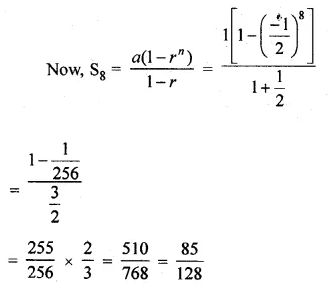
Question 11.
The first term of a G.P. is 27 and 8th term is \(\\ \frac { 1 }{ 81 } \) . Find the sum of its first 10 terms.
Solution:
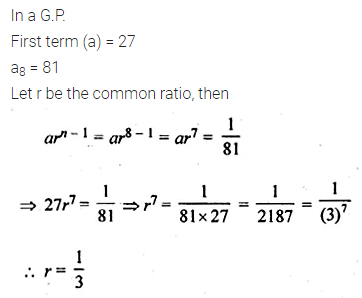
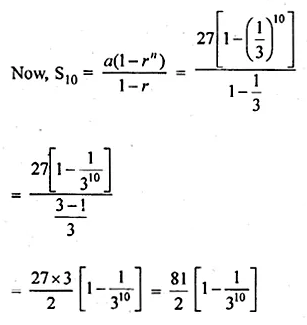
Question 12.
Find the first term of the G.P. whose common ratio is 3, the last term is 486 and the sum of those terms is 728
Solution:
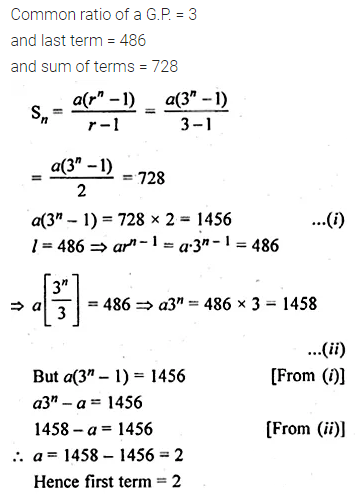
Question 13.
In a G.P. the first term is 7, the last term is 448, and the sum is 889. Find the common ratio.
Solution:

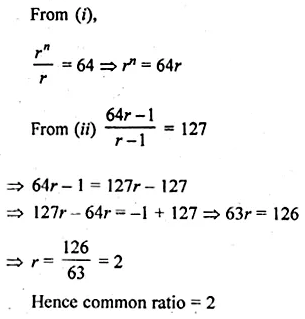
Question 14.
Find the third term of a G.P. whose common ratio is 3 and the sum of whose first seven terms is 2186.
Solution:

Question 15.
If the first term of a G.P. is 5 and the sum of first three terms is \(\\ \frac { 31 }{ 5 } \), find the common ratio.
Solution:
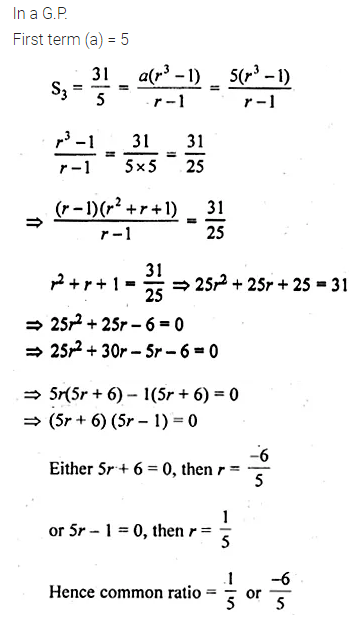
Question 16.
The sum of first three terms of a GP. is to the sum of first six terms as 125 : 152. Find the common ratio of the GP.
Solution:

Question 17.
Find the sum of the products of the corresponding terms of the geometric progression 2, 4, 8, 16, 32 and 128, 32, 8, 2, \(\\ \frac { 1 }{ 2 } \)
Solution:
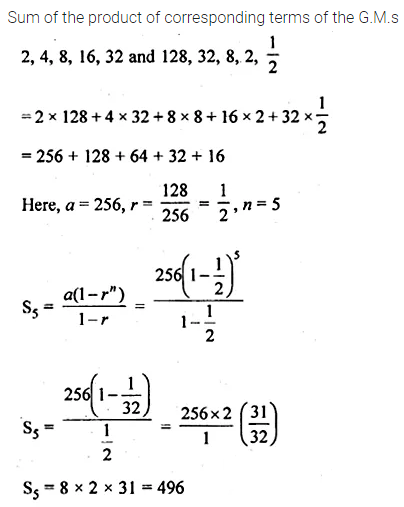
Question 18.
Evaluate \(\sum _{ n=1 }^{ 50 }{ \left( { 2 }^{ n }-1 \right) } \)
Solution:
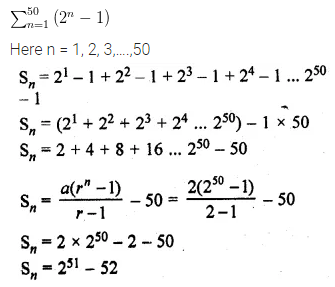
Question 19.
Find the sum of n terms of a series whose mth term is 2m + 2m.
Solution:
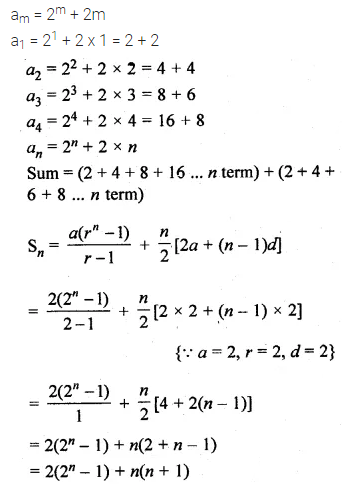
Question 20.
Sum the series
x(x + y) + x2 (x2 + y2) + x3 (x3 + y3) … to n terms.
Solution:

Question 21.
Find the sum of the series
1 + (1 + x) + (1 + x + x2) + … to n terms, x ≠ 1.
Solution:

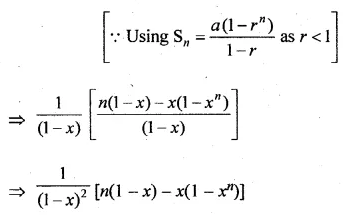
Question 22.
Find the sum of the following series to n terms:
(i) 7 + 77 + 777 + …
(ii) 8 + 88 + 888 + …
(iii) 0.5 + 0.55 + 0.555 + …
Solution: