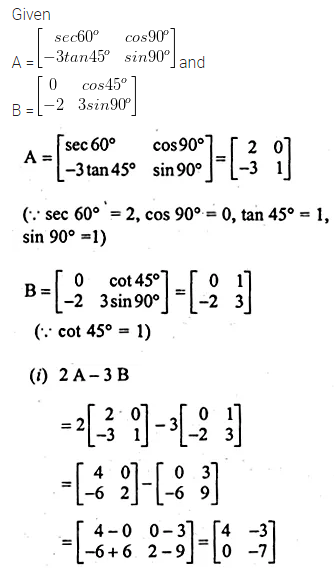ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test
Question 1.
Find the values of a and below
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
Solution:

Question 2.
Find a, b, c and d if \(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)
Solution:

Question 3.
Find X if Y = \(\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \) and 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
Solution:
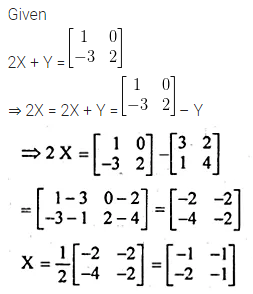
Question 4.
Determine the matrices A and B when
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) and 2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \)
Solution:

Question 5.
(i) Find the matrix B if A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \) and A² = A + 2B
(ii) If A = \(\begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix} \), B = \(\begin{bmatrix} 0 & 1 \\ -2 & 5 \end{bmatrix} \)
and C = \(\begin{bmatrix} -2 & 0 \\ -1 & 1 \end{bmatrix} \) find A(4B – 3C)
Solution:

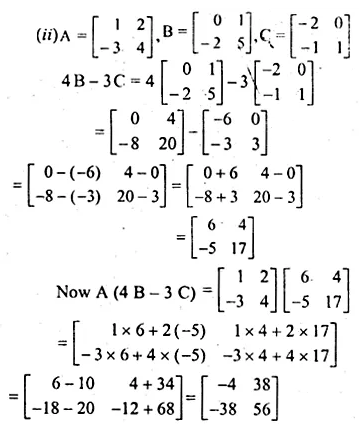
Question 6.
If A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \), B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \) compute (AB)C = (CB)A ?
Solution:
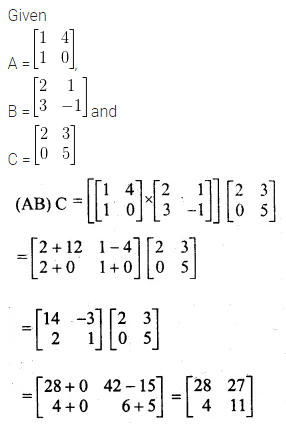
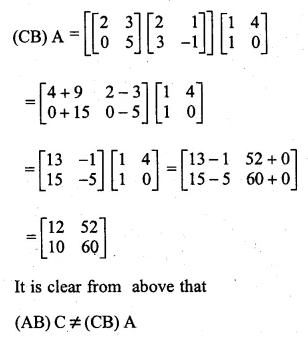
Question 7.
If A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \) find the each of the following and state it they are equal:
(i) (A + B)(A – B)
(ii)A² – B²
Solution:
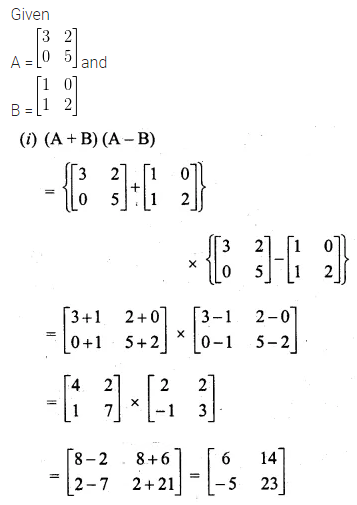
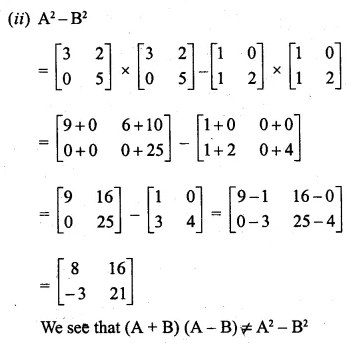
Question 8.
If A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \) find A² – 5A – 14I
Where I is unit matrix of order 2 x 2
Solution:
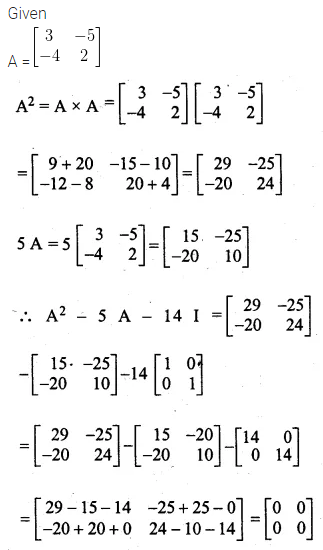
Question 9.
If A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \) and A² = 0 find p and q
Solution:

Question 10.
If A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \) and A² = I, find x,y
Solution:
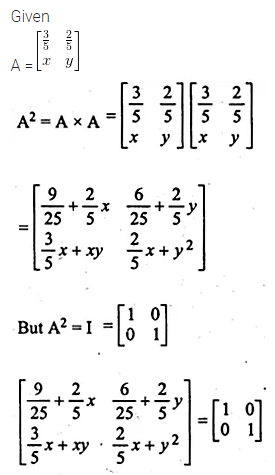
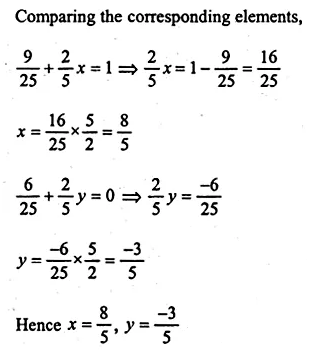
Question 11.
If \(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \) find a,b,c and d
Solution:

Question 12.
Find a and b if
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)
Solution:

Question 13.
If A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)
Find (i) 2A – 3B (ii) A² (iii) BA
Solution: