ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18
Question 1.
If A is an acute angle and sin A = \(\\ \frac { 3 }{ 5 } \) find all other trigonometric ratios of angle A (using trigonometric identities).
Solution:
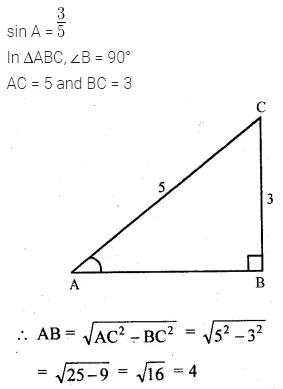
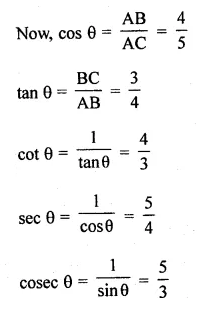
Question 2.
If A is an acute angle and sec A = \(\\ \frac { 17 }{ 8 } \), find all other trigonometric ratios of angle A (using trigonometric identities).
Solution:
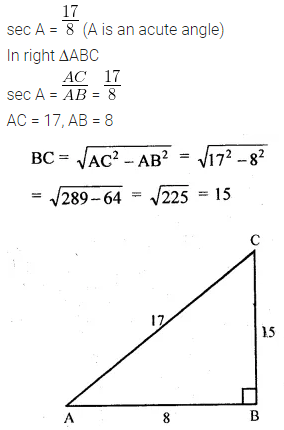
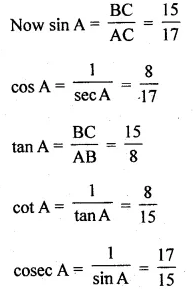
Question 3.
Express the ratios cos A, tan A and sec A in terms of sin A.
Solution:
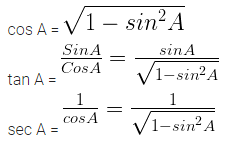
Question 4.
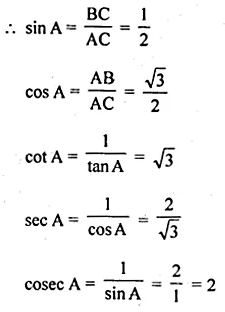
If tan A = \(\frac { 1 }{ \sqrt { 3 } } \), find all other trigonometric ratios of angle A.
Solution:
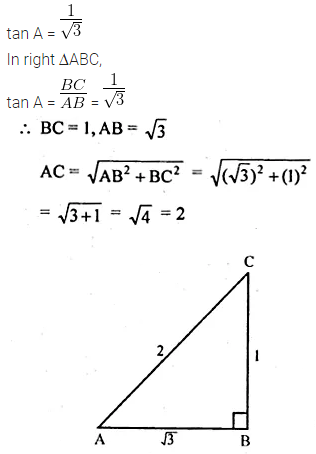
Question 5.
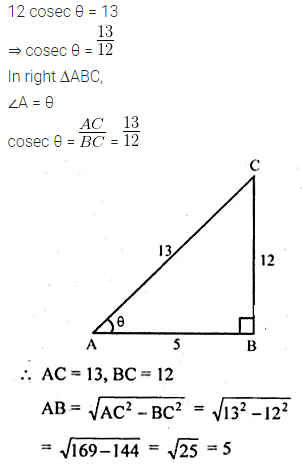
If 12 cosec θ = 13, find the value of \(\frac { 2sin\theta -3cos\theta }{ 4sin\theta -9cos\theta } \)
Solution:
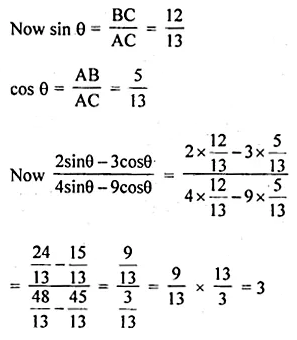
Without using trigonometric tables, evaluate the following (6 to 10):
Question 6.
(i) cos² 26° + cos 64° sin 26° + \(\frac { tan{ 36 }^{ ° } }{ { cot54 }^{ ° } } \)
(ii) \(\frac { sec{ 17 }^{ ° } }{ { cosec73 }^{ ° } } +\frac { tan68^{ ° } }{ cot22^{ ° } } \) + cos² 44° + cos² 46°
Solution:

Question 7.
(i) \(\frac { sin65^{ ° } }{ { cos25 }^{ ° } } +\frac { cos32^{ ° } }{ sin58^{ ° } } \) – sin 28° sec 62° + cosec² 30° (2015)
(ii) \(\frac { sin29^{ ° } }{ { cosec61 }^{ ° } } \) + 2 cot 8° cot 17° cot 45° cot 73° cot 82° – 3(sin² 38° + sin² 52°).
Solution:

Question 8.
(i) \(\frac { { sin }35^{ ° }{ cos55 }^{ ° }+{ cos35 }^{ ° }{ sin }55^{ ° } }{ { cosec }^{ 2 }{ 10 }^{ ° }-{ tan }^{ 2 }{ 80 }^{ ° } } \)
(ii) \({ sin }^{ 2 }{ 34 }^{ ° }+{ sin }^{ 2 }{ 56 }^{ ° }+2tan{ 18 }^{ ° }{ tan72 }^{ ° }-{ cot }^{ 2 }{ 30 }^{ ° }\)
Solution:

Question 9.
(i) \({ \left( \frac { { tan25 }^{ ° } }{ { cosec }65^{ ° } } \right) }^{ 2 }+{ \left( \frac { { cot25 }^{ ° } }{ { sec65 }^{ ° } } \right) }^{ 2 }+{ 2tan18 }^{ ° }{ tan }45^{ ° }{ tan72 }^{ ° } \)
(ii) \(\left( { cos }^{ 2 }25+{ cos }^{ 2 }65 \right) +cosec\theta sec\left( { 90 }^{ ° }-\theta \right) -cot\theta tan\left( { 90 }^{ ° }-\theta \right) \)
Solution:

Question 10.
(i) 2(sec² 35° – cot² 55°) – \(\frac { { cos28 }^{ ° }cosec{ 62 }^{ ° } }{ { tan18 }^{ ° }tan{ 36 }^{ ° }{ tan30 }^{ ° }{ tan54 }^{ ° }{ tan72 }^{ ° } } \)
(ii) \(\frac { { cosec }^{ 2 }(90-\theta )-{ tan }^{ 2 }\theta }{ 2({ cos }^{ 2 }{ 48 }^{ ° }+{ cos }^{ 2 }{ 42 }^{ ° }) } -\frac { { 2tan }^{ 2 }{ 30 }^{ ° }{ sec }^{ 2 }{ 52 }^{ ° }{ sin }^{ 2 }{ 38 }^{ ° } }{ { cosec }^{ 2 }{ 70 }^{ ° }-{ tan }^{ 2 }{ 20 }^{ ° } } \)
Solution:

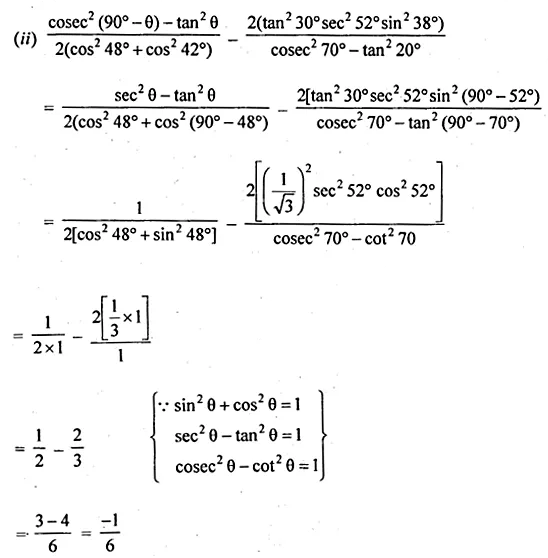
Question 11.
Prove that following:
(i) cos θ sin (90° – θ) + sin θ cos (90° – θ) = 1
(ii) \(\frac { tan\theta }{ tan({ 90 }^{ ° }-\theta ) } +\frac { sin({ 90 }^{ ° }-\theta ) }{ cos\theta } ={ sec }^{ 2 }\theta \)
(iii) \(\frac { cos({ 90 }^{ ° }-\theta )cos\theta }{ tan\theta } +{ cos }^{ 2 }({ 90 }^{ ° }-\theta )=1\)
(iv) sin (90° – θ) cos (90° – θ) = \(\frac { tan\theta }{ { 1+tan }^{ 2 }\theta } \)
Solution:
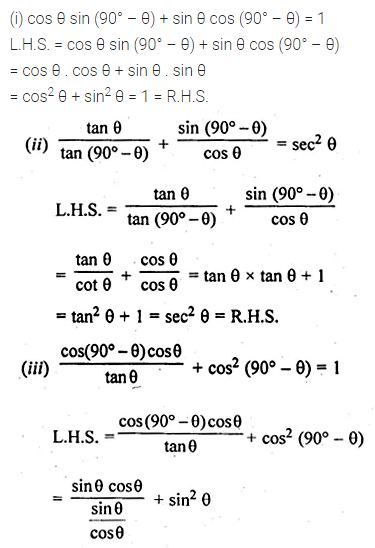
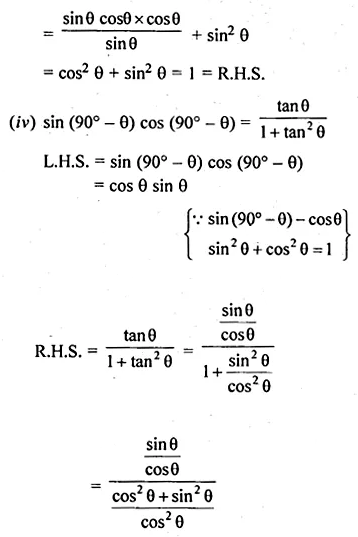
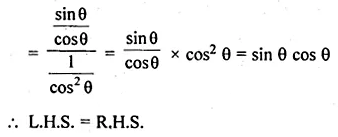
Prove that following (12 to 30) identities, where the angles involved are acute angles for which the trigonometric ratios as defined:
Question 12.
(i) (sec A + tan A) (1 – sin A) = cos A
(ii) (1 + tan2 A) (1 – sin A) (1 + sin A) = 1.
Solution:
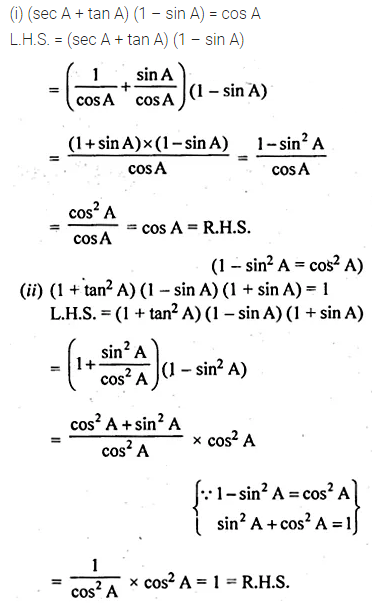
Question 13.
(i) tan A + cot A = sec A cosec A
(ii) (1 – cos A)(1 + sec A) = tan A sin A.
Solution:
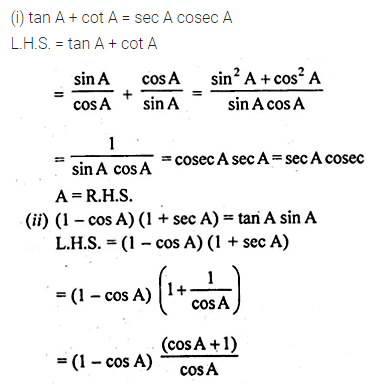
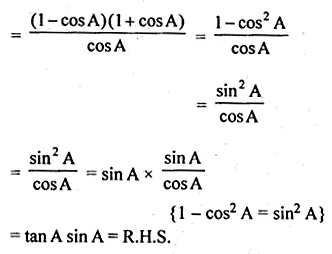
Question 14.
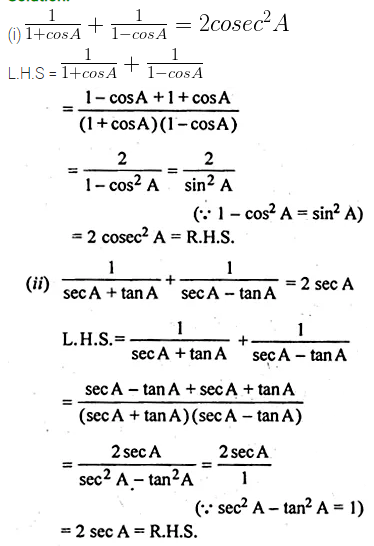
(i) \(\frac { 1 }{ 1+cosA } +\frac { 1 }{ 1-cosA } =2{ cosec }^{ 2 }A\)
(ii) \(\frac { 1 }{ secA+tanA } +\frac { 1 }{ secA-tanA } =2{ sec }A\)
Solution:
Question 15.
(i) \(\frac { sinA }{ 1+cosA } =\frac { 1-cosA }{ sinA } \)
(ii) \(\frac { 1-{ tan }^{ 2 }A }{ { cot }^{ 2 }A-1 } ={ tan }^{ 2 }A\)
(iii) \(\frac { sinA }{ 1+cosA } =cosecA-cotA\)
Solution:

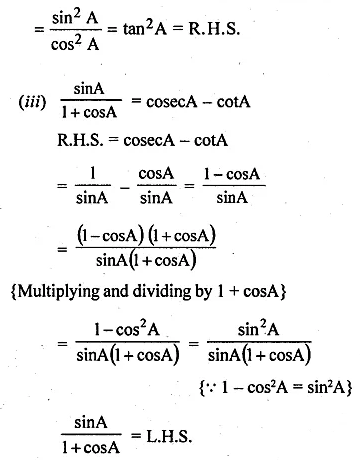
Question 16.
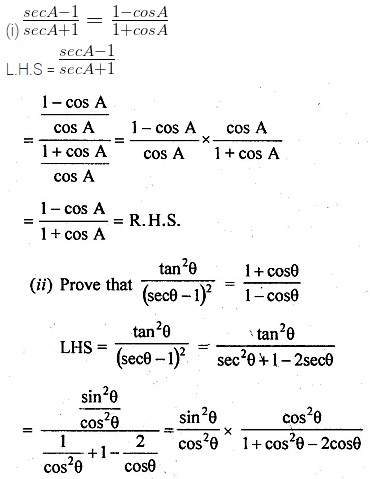
(i) \(\frac { secA-1 }{ secA+1 } =\frac { 1-cosA }{ 1+cosA } \)
(ii) \(\frac { { tan }^{ 2 }\theta }{ { (sec\theta -1) }^{ 2 } } =\frac { 1+cos\theta }{ 1-cos\theta } \)
(iii) \({ (1+tanA) }^{ 2 }+{ (1-tanA) }^{ 2 }=2{ sec }^{ 2 }A\)
(iv) \({ sec }^{ 2 }A+{ cosec }^{ 2 }A={ sec }^{ 2 }A{ .cosec }^{ 2 }A\)
Solution:
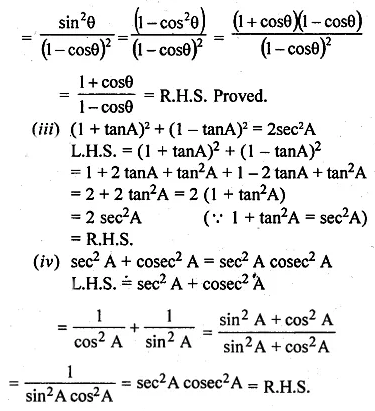
Question 17.
(i) \(\frac { 1+sinA }{ cosA } +\frac { cosA }{ 1+sinA } =2secA \)
(ii) \(\frac { tanA }{ secA-1 } +\frac { tanA }{ secA+1 } =2cosecA\)
Solution:


Question 18.
(i) \(\frac { cosecA }{ cosecA-1 } +\frac { cosecA }{ cosecA+1 } =2{ sec }^{ 2 }A\)
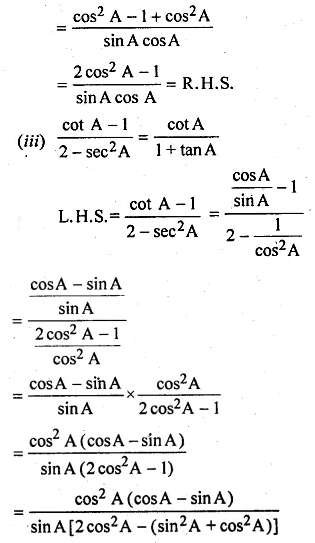
(ii) \(cotA-tanA=\frac { { 2cos }^{ 2 }A-1 }{ sinA-cosA } \)
(iii) \(\frac { cotA-1 }{ 2-{ sec }^{ 2 }A } =\frac { cotA }{ 1+tanA } \)
Solution:

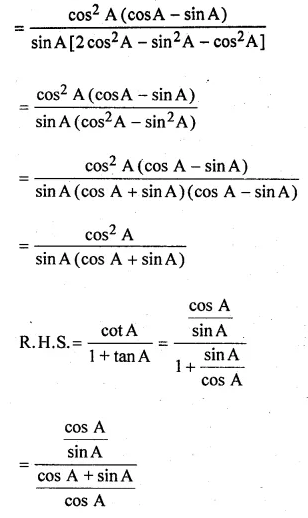
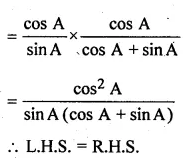
Question 19.
(i) \({ tan }^{ 2 }\theta -{ sin }^{ 2 }\theta ={ tan }^{ 2 }\theta { sin }^{ 2 }\theta \)
(ii) \(\frac { cos\theta }{ 1-tan\theta } -\frac { { sin }^{ 2 }\theta }{ cos\theta -sin\theta } =cos\theta +sin\theta \)
Solution:
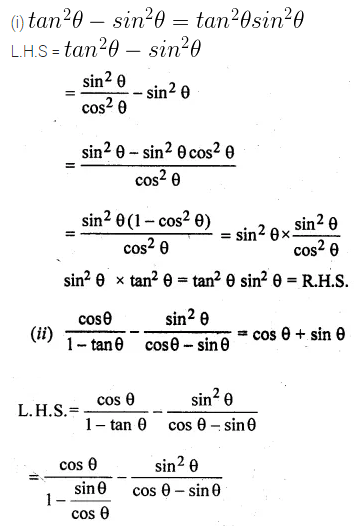
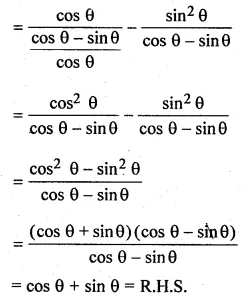
Question 20.
(i) cosec4 θ – cosec2 θ = cot4 θ + cot2 θ
(ii) 2 sec2 θ – sec4 θ – 2 cosec2 θ + cosec4 θ = cot4 θ – tan4 θ.
Solution:
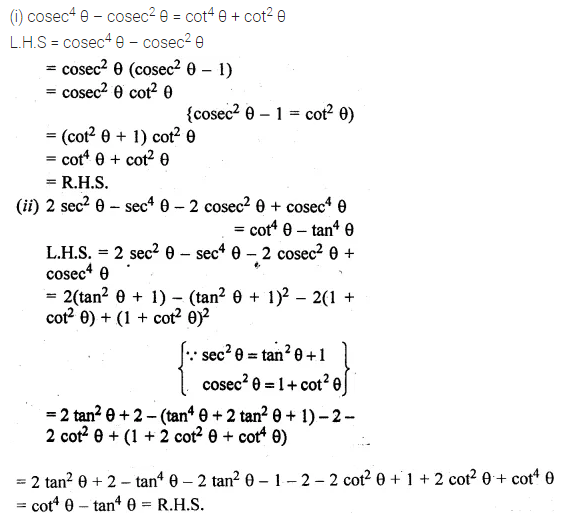
Question 21.
(i) \(\frac { 1+cos\theta -{ sin }^{ 2 }\theta }{ sin\theta (1+cos\theta ) } =cot\theta \)
(ii) \(\frac { { tan }^{ 3 }\theta -1 }{ tan\theta -1 } ={ sec }^{ 2 }\theta +tan\theta \)
Solution:
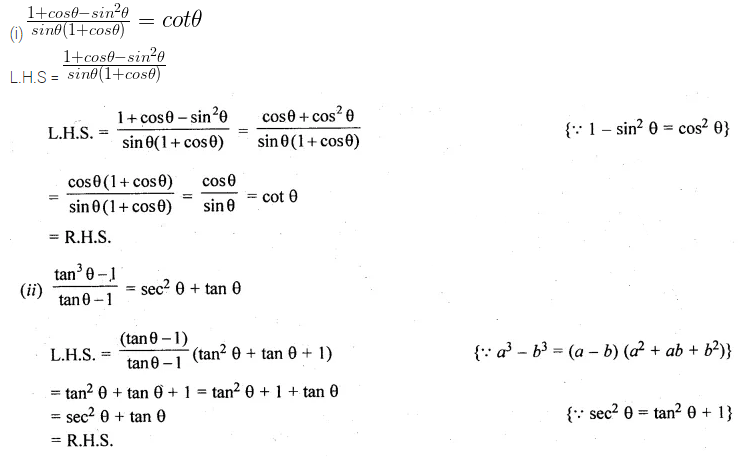
Question 22.
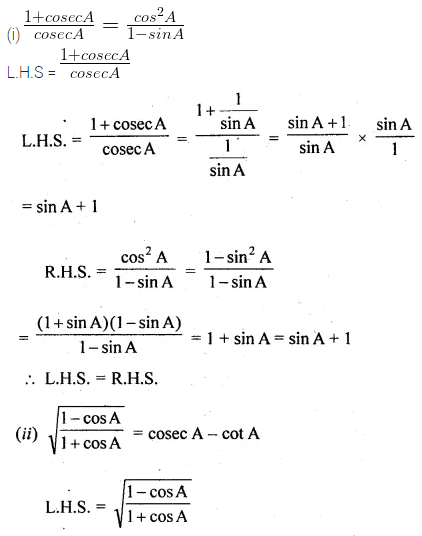
(i) \(\frac { 1+cosecA }{ cosecA } =\frac { { cos }^{ 2 }A }{ 1-sinA } \)
(ii) \(\sqrt { \frac { 1-cosA }{ 1+cosA } } =\frac { sinA }{ 1+cosA } \)
Solution:

Question 23.
(i) \(\sqrt { \frac { 1+sinA }{ 1-sinA } } =tanA+secA\)
(ii) \(\sqrt { \frac { 1-cosA }{ 1+cosA } } =cosecA-cotA\)
Solution:


Question 24.
(i) \(\sqrt { \frac { secA-1 }{ secA+1 } } +\sqrt { \frac { secA+1 }{ secA-1 } } =2cosecA\)
(ii) \(\frac { cotAcotA }{ 1-sinA } =1+cosecA \)
Solution:

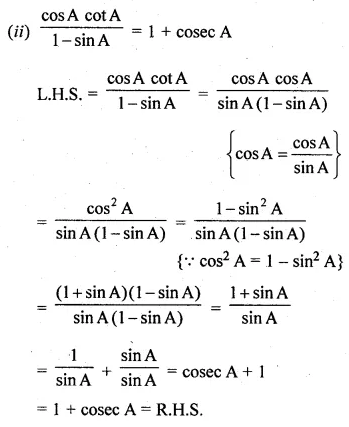
Question 25.
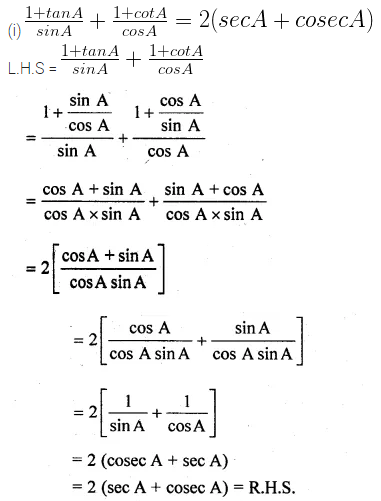
(i) \(\frac { 1+tanA }{ sinA } +\frac { 1+cotA }{ cosA } =2(secA+cosecA)\)
(ii) \({ sec }^{ 4 }A-{ tan }^{ 4 }A=1+2{ tan }^{ 2 }A \)
Solution:
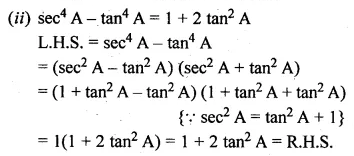
Question 26.
(i) cosec6 A – cot6 A = 3 cot2 A cosec2 A + 1
(ii) sec6 A – tan6 A = 1 + 3 tan2 A + 3 tan4 A
Solution:

Question 27.
(i) \(\frac { cot\theta -cosec\theta -1 }{ cot\theta -cosec\theta +1 } =\frac { 1+cos\theta }{ sin\theta } \)
(ii) \(\frac { sin\theta }{ cot\theta +cosec\theta } =2+\frac { sin\theta }{ cot\theta -cosec\theta } \)
Solution:
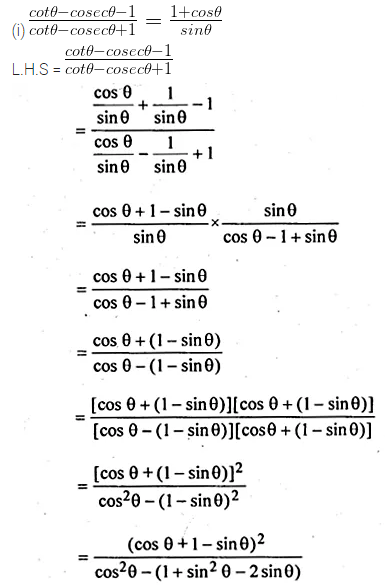
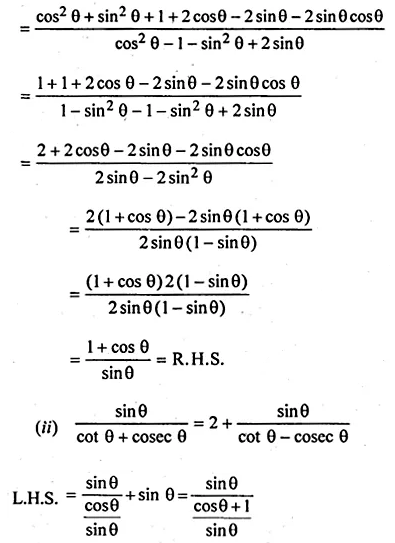
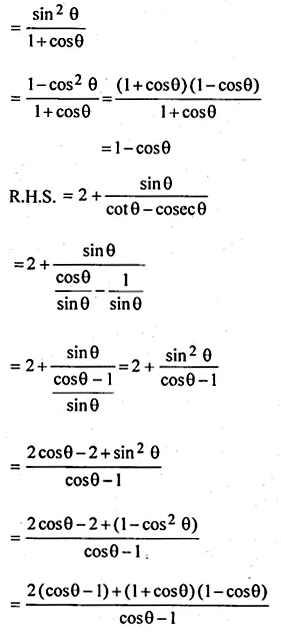
Question 28.
(i) (sinθ + cosθ)(secθ + cosecθ) = 2 + secθ cosecθ
(ii) (cosecA – sinA)(secA – cosA) sec2A = tanA
(iii) (cosecθ – sinθ)(secθ – cosθ)(tan θ + cotθ) = 1
Solution:


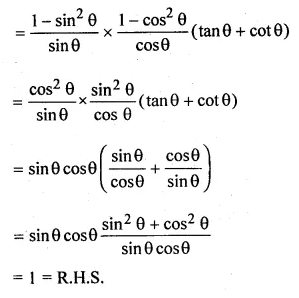
Question 29.
(i) \(\frac { { sin }^{ 3 }A+{ cos }^{ 3 }A }{ sinA+cosA } +\frac { { sin }^{ 3 }A-{ cos }^{ 3 }A }{ sinA-cosA } =2\)
(ii) \(\frac { { tan }^{ 2 }A }{ { 1+tan }^{ 2 }A } +\frac { cot^{ 2 }A }{ 1+{ cot }^{ 2 }A } =1\)
Solution:
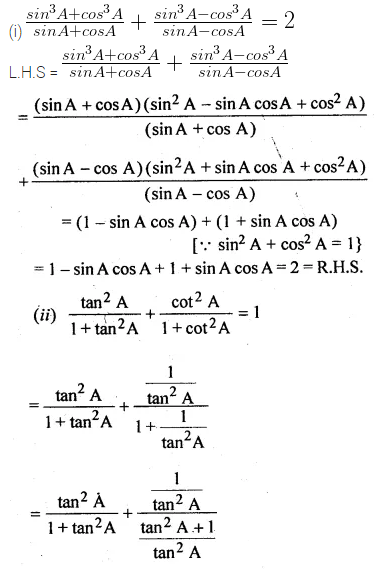
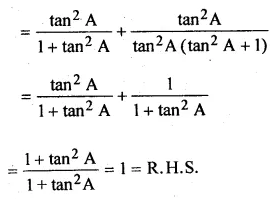
Question 30.
(i) \(\frac { 1 }{ secA+tanA } -\frac { 1 }{ cosA } =\frac { 1 }{ cosA } -\frac { 1 }{ secA-tanA } \)
(ii) \({ (sinA+secA) }^{ 2 }+{ (cosA+cosecA) }^{ 2 }={ (1+secA\quad cosecA) }^{ 2 }\)
(iii) \(\frac { tanA+sinA }{ tanA-sinA } =\frac { secA+1 }{ secA-1 } \)
Solution:
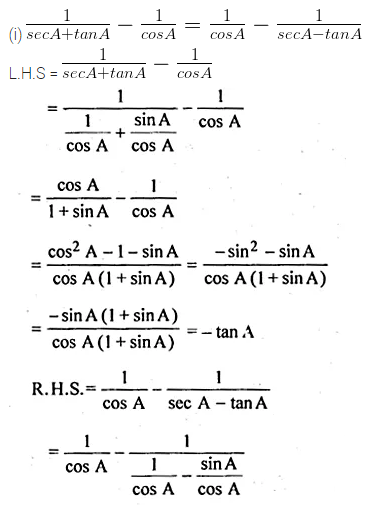
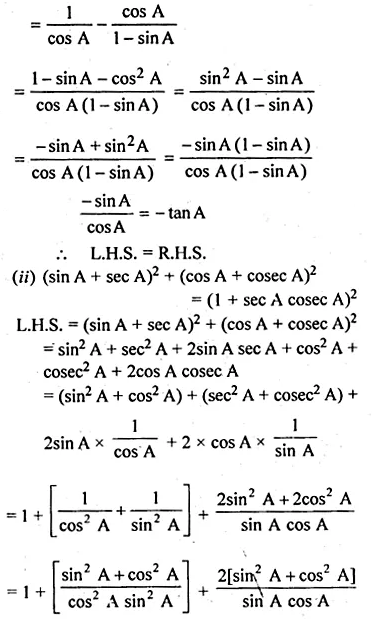


Question 31.
If sin θ + cos θ = √2 sin (90° – θ), show that cot θ = √2 + 1
Solution:
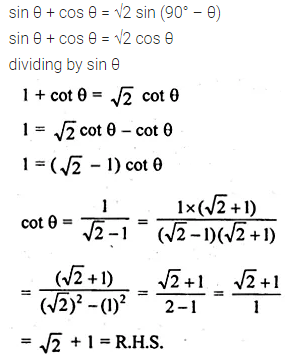
Question 32.
If 7 sin2 θ + 3 cos2 θ = 4, 0° ≤ θ ≤ 90°, then find the value of θ.
Solution:
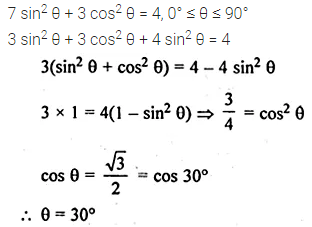
Question 33.
If sec θ + tan θ = m and sec θ – tan θ = n, prove that mn = 1.
Solution:

Question 34.
If x – a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x2 – y2 = a2 – b2.
Solution:
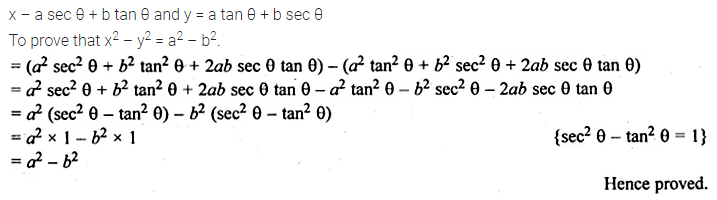
Question 35.
If x = h + a cos θ and y = k + a sin θ, prove that (x – h)2 + (y – k)2 = a2.
Solution:
