ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS

Choose the correct answer from the given four options (1 to 32):

Question 1.
In a cylinder, if the radius is halved and height is doubled then the volume will be
(a) same
(b) doubled
(c) halved
(d) four times
Solution:

Question 2.
In a cylinder, if the radius is doubled &nd height is halved then its curved surface area will be
(a) halved
(b) doubled
(c) same
(d) four times
Solution:

Question 3.
If a well of diameter 8 m has been dug to the depth of 14 m, then the volume of the earth dug out is
(a) 352 m³
(b) 704 m³
(c) 1408 m³
(d) 2816 m³
Solution:

Question 4.
If two cylinders of the same lateral surface have their radii in the ratio 4 : 9, then the ratio of their heights is
(a) 2 : 3
(b) 3 : 2
(c) 4 : 9
(d) 9 : 4
Solution:

Question 5.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is
(a) 10 : 17
(b) 20 : 27
(c) 17 : 27
(d) 20 : 37
Solution:

Question 6.
The total surface area of a cone whose radius is \(\\ \frac { r }{ 2 } \) and slant height 2l is
(a) 2πr (l + r)
(b) \(\pi r\left( l+\frac { r }{ 4 } \right) \)
(c) πr(l + r)
(d) 2πrl
Solution:

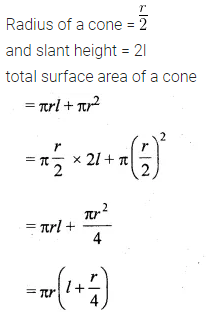
Question 7.
If the diameter of the base of cone is 10 cm and its height is 12 cm, then its curved surface area is
(a) 60π cm²
(b) 65π cm²
(c) 90π cm²
(d) 120π cm²
Solution:

Question 8.
If the diameter of the base of a cone is 12 cm and height is 20 cm, then its volume is ,
(a) 240π cm³
(b) 480π cm³
(c) 720π cm³
(d) 960π cm³
Solution:

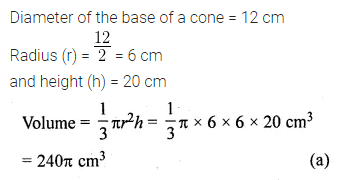
Question 9.
If the radius of a sphere is 2r, then its volume will be
(a) \(\frac { 4 }{ 3 } \pi { r }^{ 3 } \)
(b) \(4\pi { r }^{ 3 }\)
(c) \(\frac { 8\pi { r }^{ 3 } }{ 3 } \)
(d) \(\frac { 32\pi { r }^{ 3 } }{ 3 } \)
Solution:

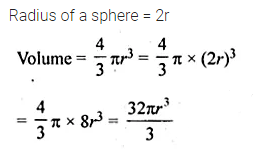
Question 10.
If the diameter of a sphere is 16 cm, then its surface area is
(a) 64π cm²
(b) 256π cm²
(c) 192π cm²
(d) 256 cm²
Solution:

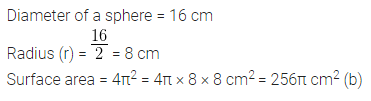
Question 11.
If the radius of a hemisphere is 5 cm, then its volume is
(a) \(\frac { 250 }{ 3 } \pi { \quad cm }^{ 3 }\)
(b) \(\frac { 500 }{ 3 } \pi { \quad cm }^{ 3 } \)
(c) \(75\pi { \quad cm }^{ 3 } \)
(d) \(\frac { 125 }{ 3 } \pi { \quad cm }^{ 3 } \)
Solution:

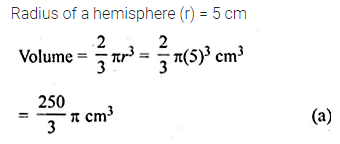
Question 12.
If the ratio of the diameters of the two spheres is 3 : 5, then the ratio of their surface areas is
(a) 3 : 5
(b) 5 : 3
(c) 27 : 125
(d) 9 : 25
Solution:

Question 13.
The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratio of the surface areas of the balloon in the two cases is
(a) 1 : 4
(b) 1 : 3
(c) 2 : 3
(d) 2 : 1
Solution:

Question 14.
The shape of a gilli, in the the game of gilli- danda, is a combination of

(a) two cylinders
(b) a cone and a cylinders
(c) two cones and a cylinder
(d) two cylinders and a cone
Solution:

Question 15.
If two solid hemisphere of same base radius r are joined together along with their bases, then the curved surface of this new solid is
(a) 4πr²
(b) 6πr²
(c) 3πr²
(d) 8πr²
Solution:

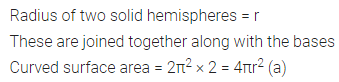
Question 16.
During the conversion of a solid from one shape to another, the volume of the new shape will
(a) increase
(b) decrease
(c) remain unaltered
(d) be doubled
Solution:

Question 17.
If a solid of one shape is converted to another, then the surface area of the new solid
(a) remains same
(b) increases
(c) decreases
(d) can’t say
Solution:

Question 18.
If a marble of radius 2.1 cm is put into a cylindrical cup full of water of radius 5 cm and height 6 cm, then the volume of water that flows out of the cylindrical cup is
(a) 38.8 cm³
(b) 55.4 cm³
(c) 19.4 cm³
(d) 471.4 cm³
Solution:

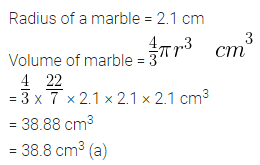
Question 19.
The volume of the largest right circular cone that can be carved out from a cube of edge 4.2 cm is
(a) 9.7 cm³
(b) 77.6 cm³
(c) 58.2 cm³
(d) 19.4 cm³
Solution:

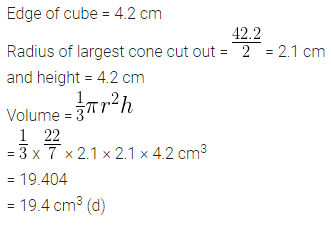
Question 20.
The volume of the greatest sphere cut off from a circular cylindrical wood of base radius 1 cm and height 6 cm is
(a) 288 π cm³
(b) \(\frac { 4 }{ 3 } \pi \) cm³
(c) 6 π cm³
(d) 4 π cm³
Solution:

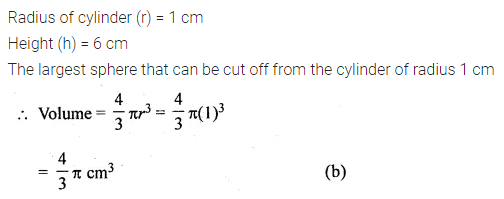
Question 21.
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) 16 : 9
Solution:

Question 22.
If a cone, a hemisphere and a cylinder have equal bases and have same height, then the ratio of their volumes is
(a) 1 : 3 : 2
(b) 2 : 3 : 1
(c) 2 : 1 : 3
(d) 1 : 2 : 3
Solution:

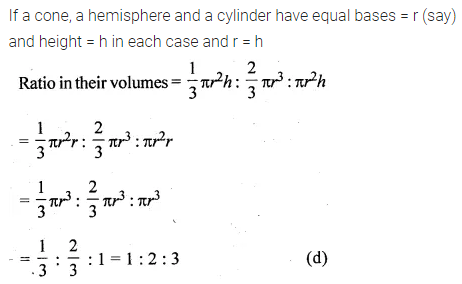
Question 23.
If a sphere and a cube have equal surface areas, then the ratio of the diameter of the sphere to the edge of the cube is
(a) 1 : 2
(b) 2 : 1
(c) √π : √6
(d) √6 : √π
Solution:

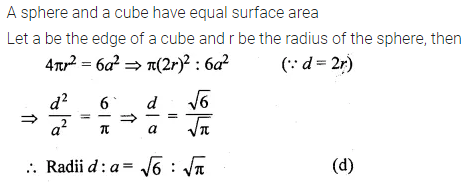
Question 24.
A solid piece of iron in the form of a cuboid of dimensions 49 cm x 33 cm x 24 cm is moulded to form a sphere. The radius of the sphere is
(a) 21 cm
(b) 23 cm
(c) 25 cm
(d) 19 cm
Solution:

Question 25.
If a solid right circular cone of height 24 cm and base radius 6 cm is melted and recast in the shape of a sphere, then the radius of the sphere is
(a) 4 cm
(b) 6 cm
(c) 8 cm
(d) 12 cm
Solution:

Question 26.
If a solid circular cylinder of iron whose diameter is 15 cm and height 10 cm is melted and recasted into a sphere, then the radius of the sphere is
(a) 15 cm
(b) 10 cm
(c) 7.5 cm
(d) 5 cm
Solution:

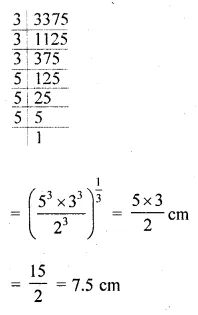
Question 27.
The number of balls of radius 1 cm that can be made from a sphere of radius 10 cm is
(a) 100
(b) 1000
(c) 10000
(d) 100000
Solution:

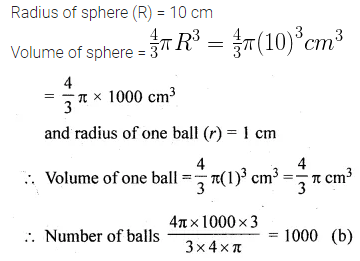
Question 28.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form of a cone of base diameter 8 cm. The height of the cone is
(a) 12 cm
(b) 14 cm
(c) 15 cm
(d) 18 cm
Solution:

Question 29.
A cubical icecream brick of edge 22 cm is to be distributed among some children by filling ice cream cones of radius 2 cm and height 7 cm up to its brim. The number of children who will get the ice cream cones is
(a) 163
(b) 263
(c) 363
(d) 463
Solution:

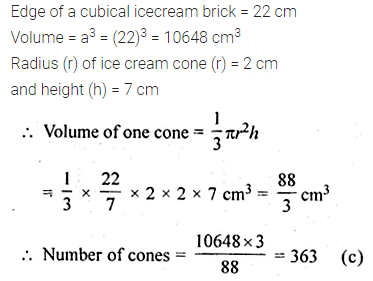
Question 30.
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is
(a) 4 cm
(b) 3 cm
(b) 2 cm
(d) 6 cm
Solution:

Question 31.
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that \(\\ \frac { 1 }{ 8 } \) space of the cube remains unfilled. Then the number of marbles that the cube can accommodate is
(a) 142296
(b) 142396
(c) 142496
(d) 142596
Solution:

Question 32.
In the given figure, the bottom of the glass has a hemispherical raised portion. If the glass is filled with orange juice, the quantity of juice which a person will get is
(a) 135 π cm³
(b) 117 π cm³
(c) 99 π cm³
(d) 36 π cm³

Solution:

ML Aggarwal Class 10 Solutions for ICSE Maths