ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1
Question 1.
Using the given information, find the value of x in each of the following figures :
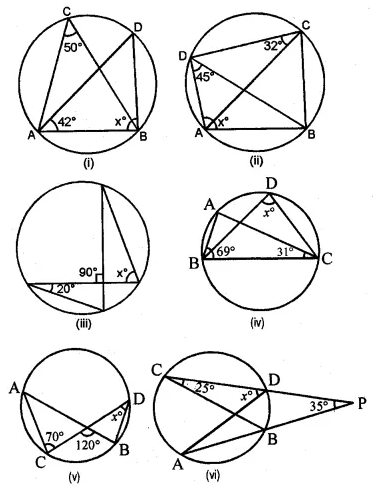
Solution:



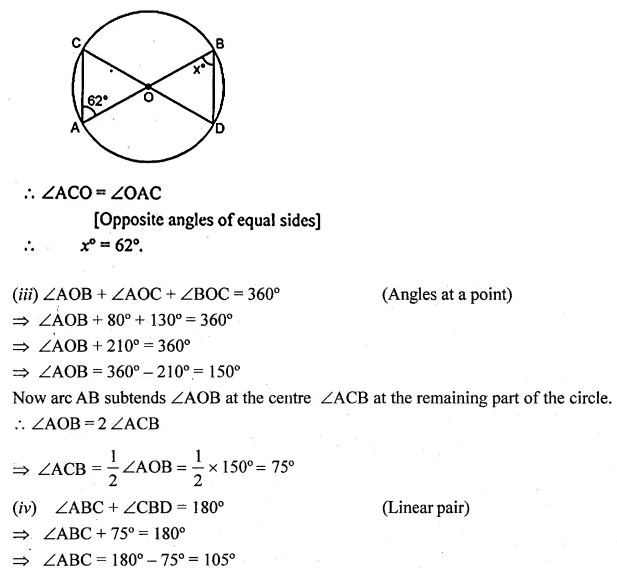
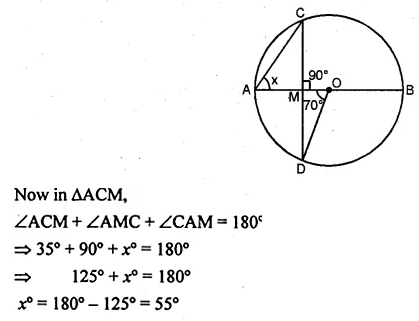
Question 2.
If O is the centre of the circle, find the value of x in each of the following figures (using the given information):
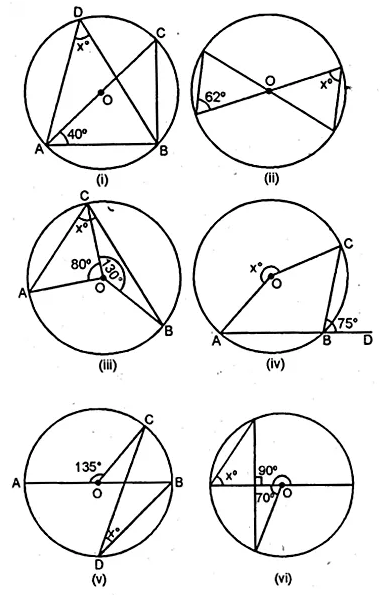
Solution:
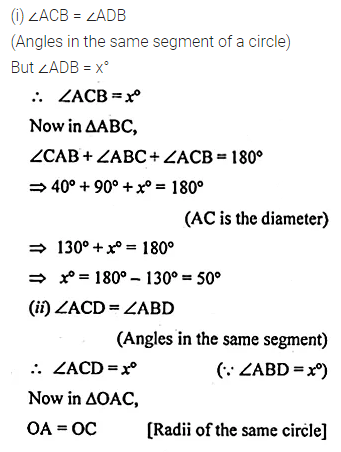

Question 3.
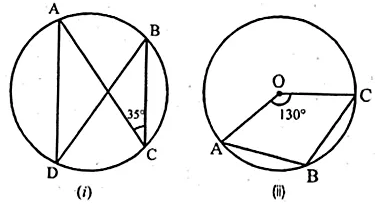
(a) In the figure (i) given below, AD || BC. If ∠ACB = 35°. Find the measurement of ∠DBC.
(b) In the figure (ii) given below, it is given that O is the centre of the circle and ∠AOC = 130°. Find∠ABC
Solution:

Question 4.
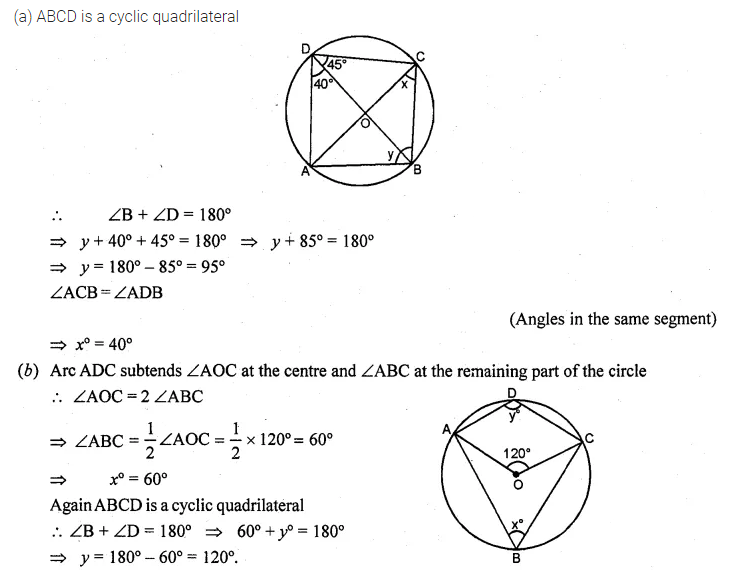
(a) In the figure (i) given below, calculate the values of x and y.
(b) In the figure (ii) given below, O is the centre of the circle. Calculate the values of x and y.
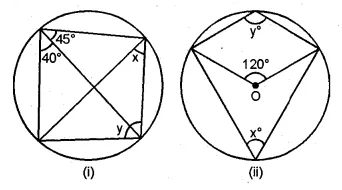
Solution:
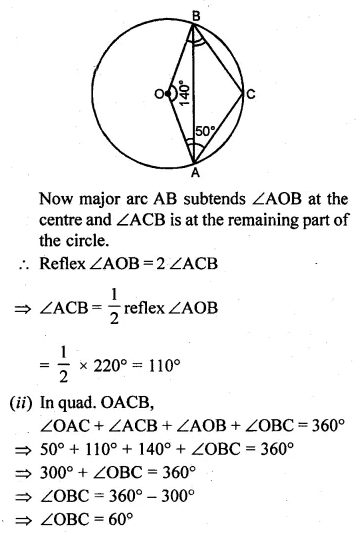
Question 5.
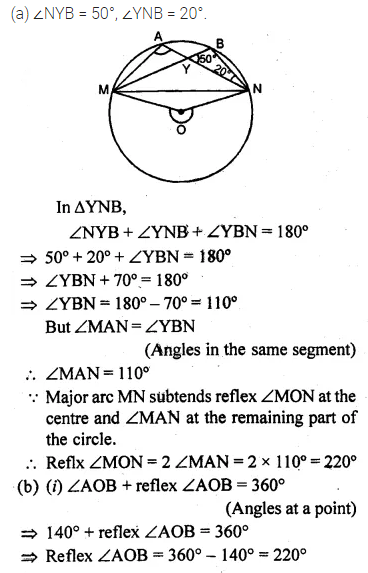
(a) In the figure (i) given below, M, A, B, N are points on a circle having centre O. AN and MB cut at Y. If ∠NYB = 50° and ∠YNB = 20°, find ∠MAN and the reflex angle MON.
(b) In the figure (ii) given below, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°, find
(i) ∠ACB
(ii) ∠OBC
(iii) ∠OAB
(iv) ∠CBA
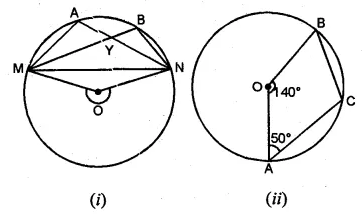
Solution:

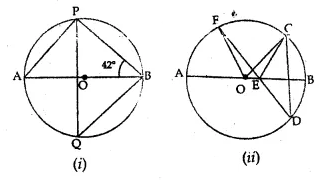
Question 6.
(a) In the figure (i) given below, O is the centre of the circle and ∠PBA = 42°. Calculate the value of ∠PQB
(b) In the figure (ii) given below, AB is a diameter of the circle whose centre is O. Given that ∠ECD = ∠EDC = 32°, calculate
(i) ∠CEF
(ii) ∠COF.
Solution:

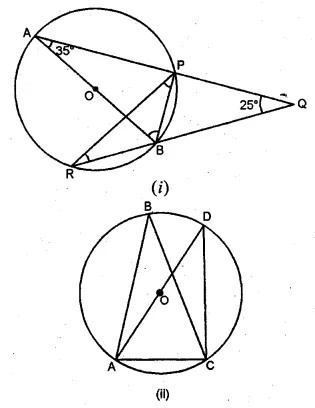
Question 7.
(a) In the figure (i) given below, AB is a diameter of the circle APBR. APQ and RBQ are straight lines, ∠A = 35°, ∠Q = 25°. Find (i) ∠PRB (ii) ∠PBR (iii) ∠BPR.
(b) In the figure (ii) given below, it is given that ∠ABC = 40° and AD is a diameter of the circle. Calculate ∠DAC.
Solution:

Question 8.
(a) In the figure given below, P and Q are centres of two circles intersecting at B and C. ACD is an st. line. Calculate the numerical value of x.
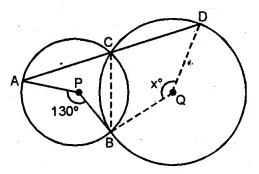
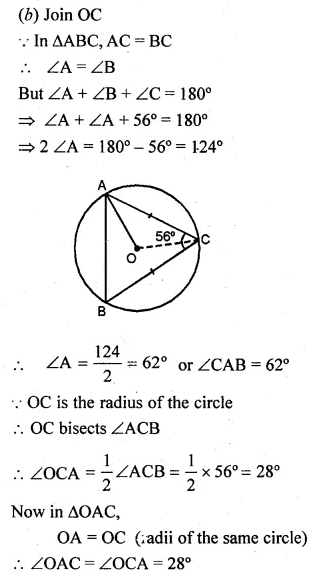
(b) In the figure given below, O is the circumcentre of triangle ABC in which AC = BC. Given that ∠ACB = 56°, calculate
(i)∠CAB
(ii)∠OAC
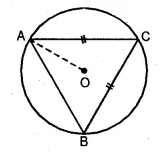
Solution:

Question 9.
(a) In the figure (i) given below, chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
(b) In the figure (ii) given below, C is a point on the minor arc AB of the circle with centre O. Given ∠ACB = p°, ∠AOB = q°, express q in terms of p. Calculate p if OACB is a parallelogram.
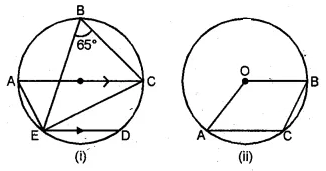
Solution:

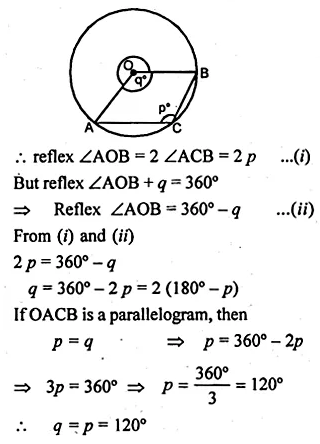
Question 10.
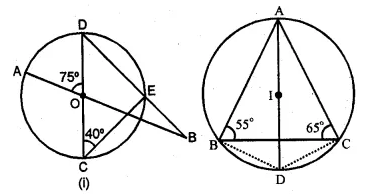
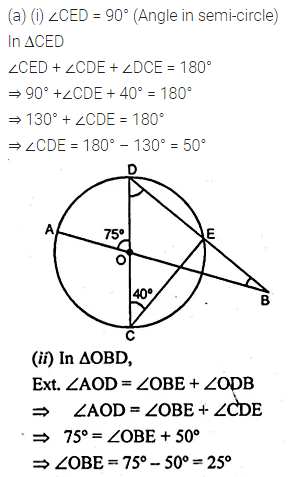
(a) In the figure (i) given below, straight lines AB and CD pass through the centre O of a circle. If ∠OCE = 40° and ∠AOD = 75°, find the number of degrees in :
(i) ∠CDE
(ii) ∠OBE.
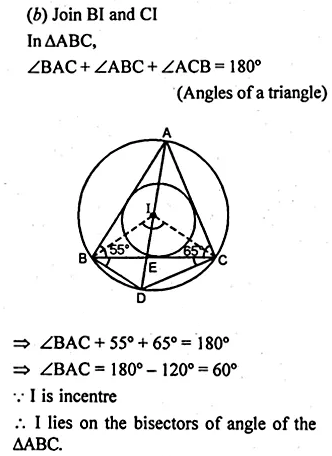
(b) In the figure (ii) given below, I is the incentre of ∆ABC. AI produced meets the circumcircle of ∆ABC at D. Given that ∠ABC = 55° and ∠ACB = 65°, calculate
(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC.
Solution:
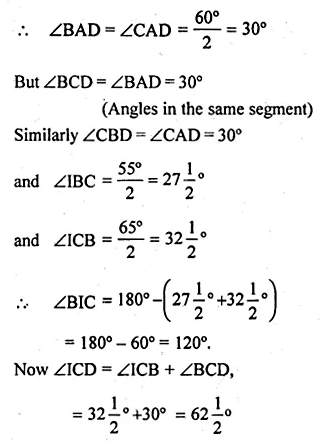
Question 11.
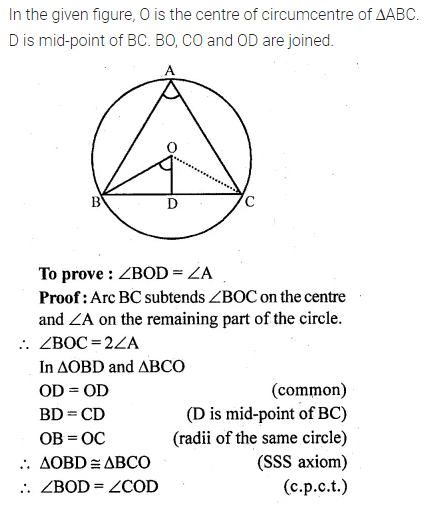
O is the circumcentre of the triangle ABC and D is mid-point of the base BC. Prove that ∠BOD = ∠A.
Solution:
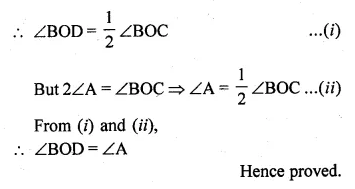
Question 12.
In the given figure, AB and CD are equal chords. AD and BC intersect at E. Prove that AE = CE and BE = DE.
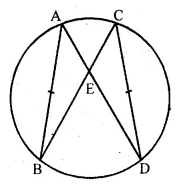
Solution:

Question 13.
(a) In the figure (i) given below, AB is a diameter of a circle with centre O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED.
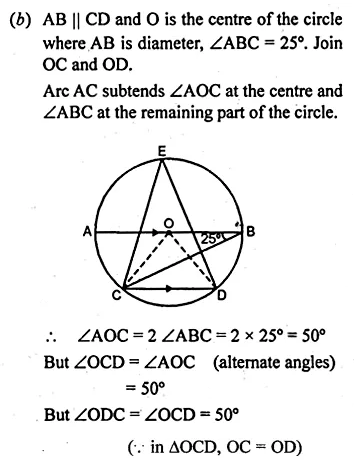
(b) In the figure (ii) given below, O is the centre of a circle. Chord CD is parallel to the diameter AB. If ∠ABC = 25°, calculate ∠CED.
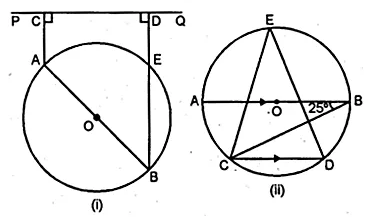
Solution:
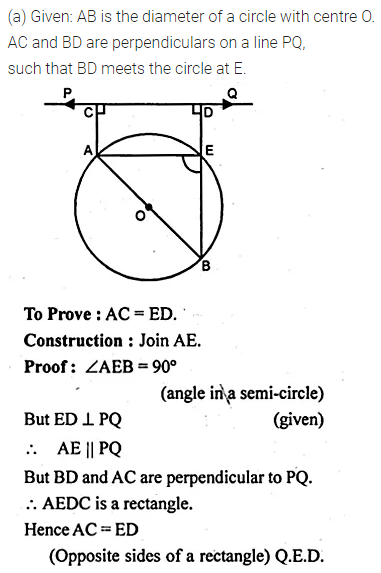

Question 14.
In the adjoining figure, O is the centre of the given circle and OABC is a parallelogram. BC is produced to meet the circle at D. Prove that ∠ABC = 2 ∠OAD.
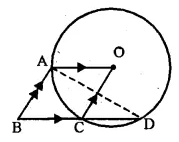
Solution:

Question 15.
(a) In the figure (i) given below, P is the point of intersection of the chords BC and AQ such that AB = AP. Prove that CP = CQ
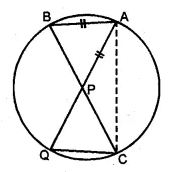
(b) In the figure (i) given below, AB = AC = CD, ∠ADC = 38°. Calculate :
(i) ∠ABC (ii) ∠BEC.
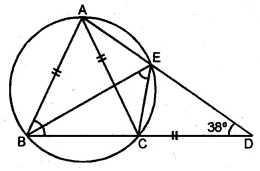
Solution:


Question 16.
(a) In the figure (i) given below, CP bisects ∠ACB. Prove that DP bisects ∠ADB.
(b) In the figure (ii) given below, BDbisects ∠ABC. Prove that \(\frac { AB }{ BD } =\frac { BE }{ BC } \)
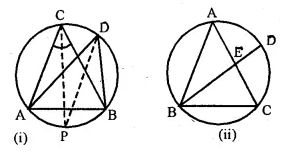
Solution:
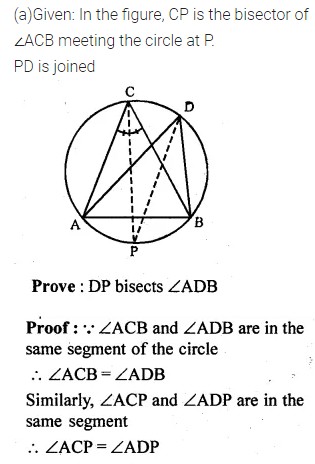
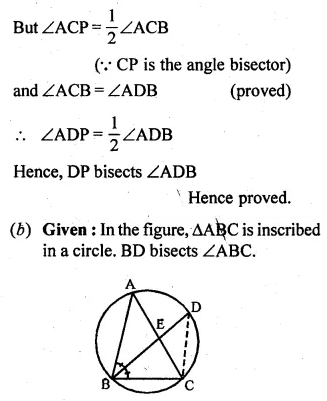

Question 17.
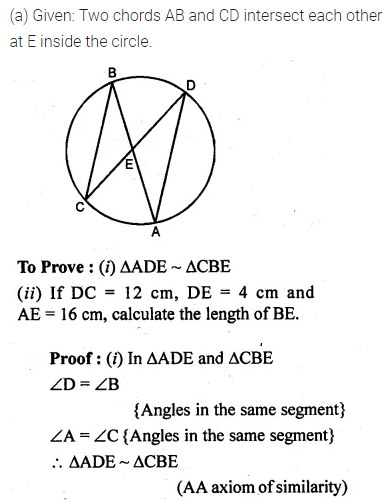
(a) In the figure (i) given below, chords AB and CD of a circle intersect at E.
(i) Prove that triangles ADE and CBE are similar.
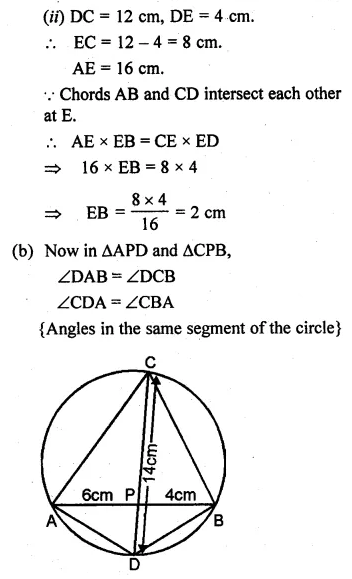
(ii) Given DC =12 cm, DE = 4 cm and AE = 16 cm, calculate the length of BE.
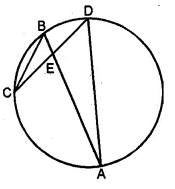
(b) In the figure (ii) given below, AB and CD are two intersecting chords of a circle. Name two triangles which are similar. Hence, calculate CP given that AP = 6 cm, PB = 4 cm, and CD = 14 cm (PC > PD).
Solution:

Question 18.
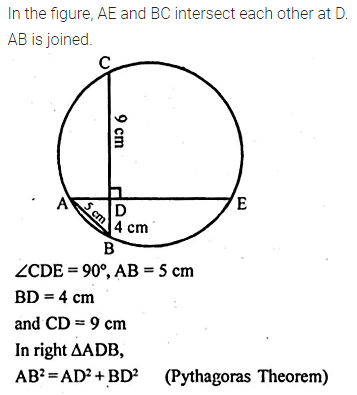
In the adjoining figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find DE. (2008)
Solution:

Question 19.
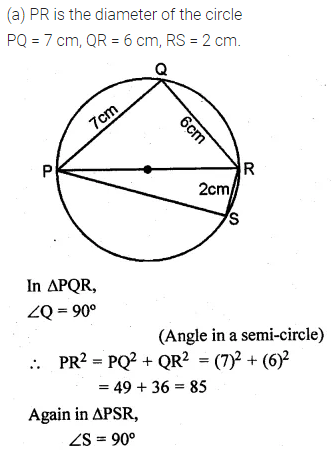
(a) In the figure (i) given below, PR is a diameter of the circle, PQ = 7 cm, QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.
(b) In the figure (ii) given below, the diagonals of a cyclic quadrilateral ABCD intersect in P and the area of the triangle APB is 24 cm². If AB = 8 cm and CD = 5 cm, calculate the area of ∆DPC.
Solution:
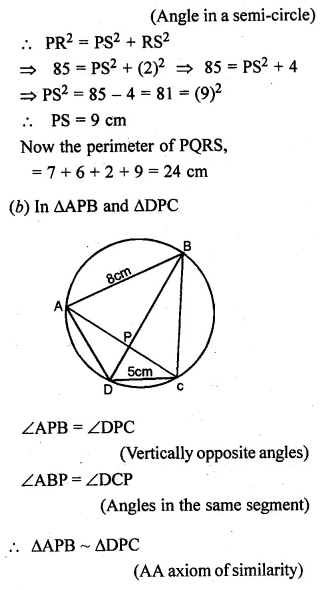

Question 20.
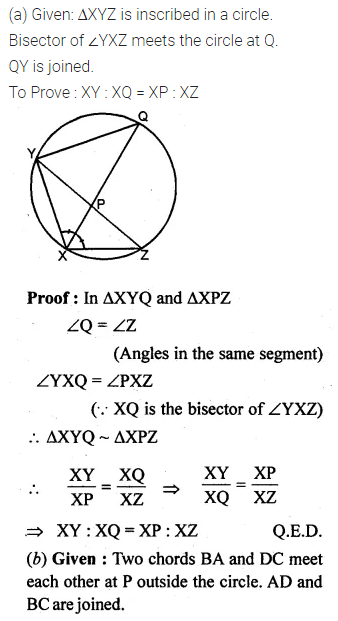
(a) In the figure (i) given below, QPX is the bisector of ∠YXZ of the triangle XYZ. Prove that XY : XQ = XP : XZ,
(b) In the figure (ii) given below, chords BA and DC of a circle meet at P. Prove that:
(i) ∠PAD = ∠PCB
(ii) PA. PB = PC . PD.
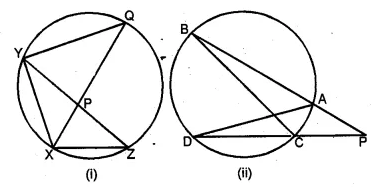
Solution: