ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14
Question 1.
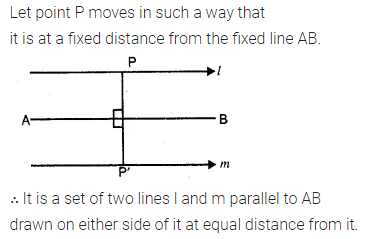
A point moves such that its distance from a fixed line AB is always the same. What is the relation between AB and the path travelled by P?
Solution:
Question 2.
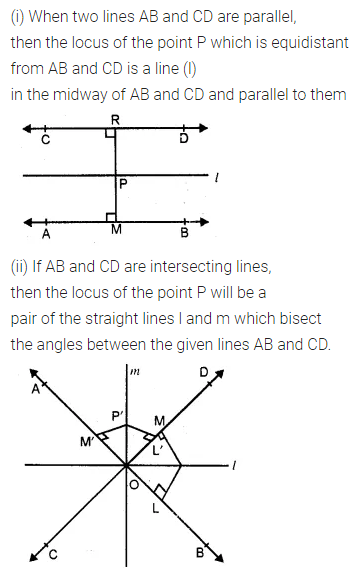
A point P moves so that its perpendicular distance from two given lines AB and CD are equal. State the locus of the point P.
Solution:
Question 3.
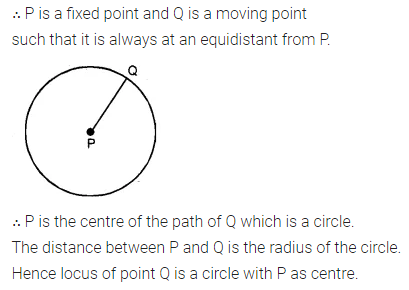
P is a fixed point and a point Q moves such that the distance PQ is constant, what is the locus of the path traced out by the point Q?
Solution:
Question 4.
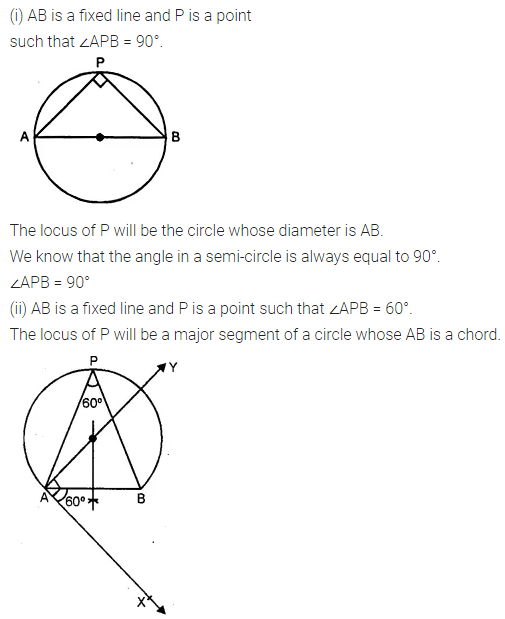
(i) AB is a fixed line. State the locus of the point P so that ∠APB = 90°.
(ii) A, B are fixed points. State the locus of the point P so that ∠APB = 60°.
Solution:
Question 5.
Draw and describe the locus in each of the following cases :
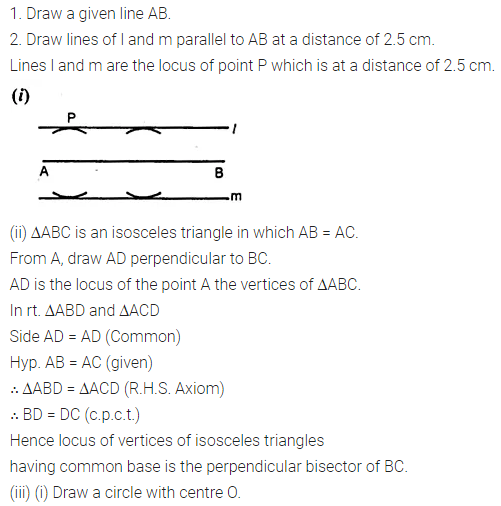
(i) The locus of points at a distance 2.5 cm from a fixed line.
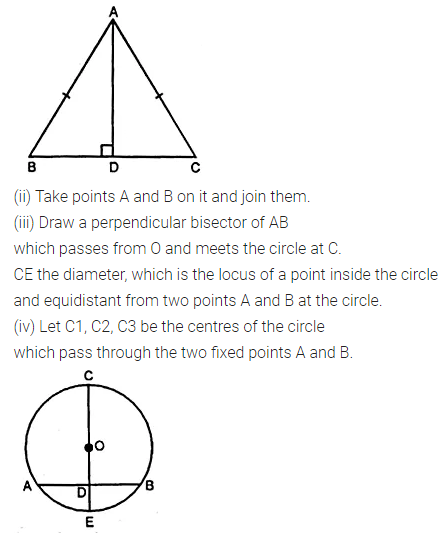
(ii) The locus of vertices of all isosceles triangles having a common base.
(iii) The locus of points inside a circle and equidistant from two fixed points on the circle.
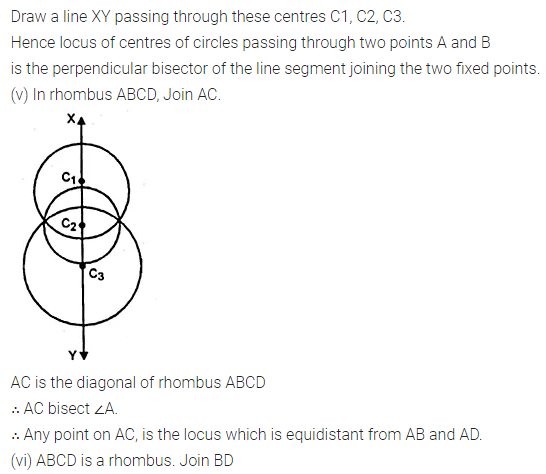
(iv) The locus of centres of all circles passing through two fixed points.
(v) The locus of a point in rhombus ABCD which is equidistant from AB and AD. (1998)
(vi) The locus of a point in the rhombus ABCD which is equidistant from points A and C.
Solution:
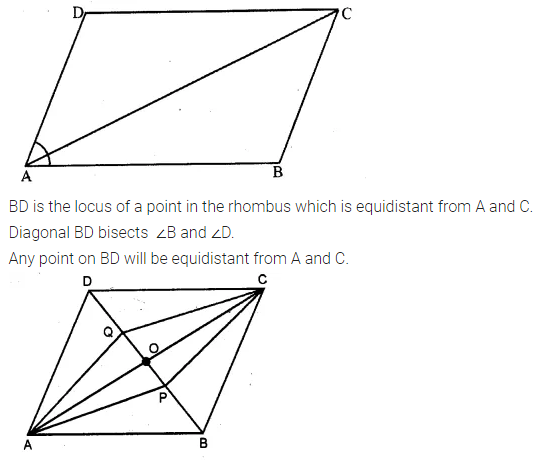
Question 6.
Describe completely the locus of points in each of the following cases :
(i) mid-point of radii of a circle.
(ii) centre of a ball, rolling along a straight line on a level floor.
(iii) the point in a plane equidistant from a given line.
(iv) the point in a plane, at a constant distance of 5 cm from a fixed point (in the plane).
(v) centre of a circle of varying radius and touching two arms of ∠ADC.
(vi) centre of a circle of varying radius and touching a fixed circle, centre O, at a fixed point A on it.
(vii) centre of a circle of radius 2 cm and touching a fixed circle of radius 3 cm with centre 0.
Solution:

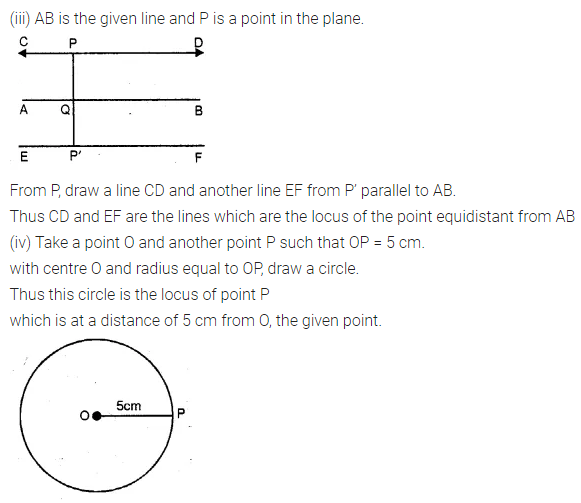
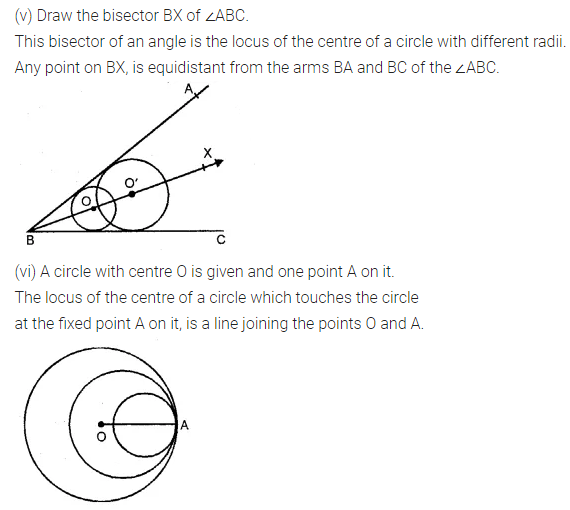
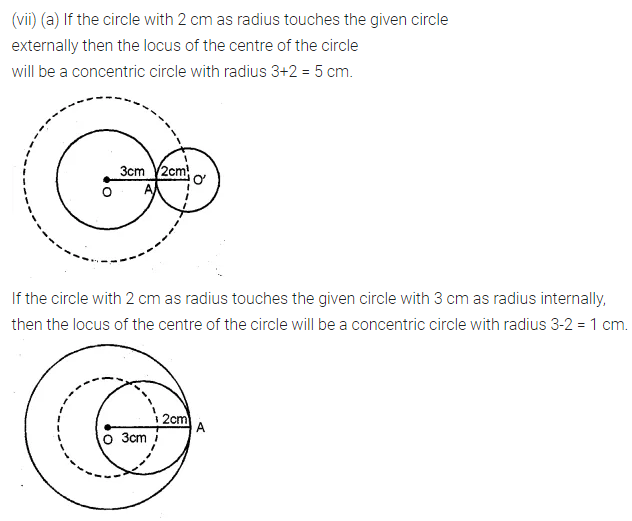
Question 7.
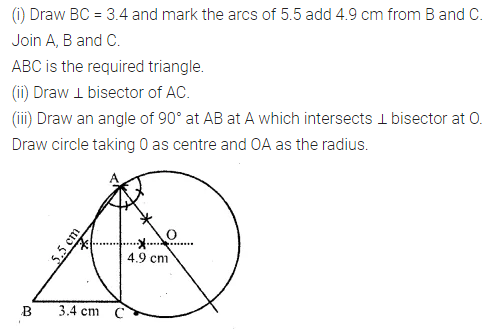
Using a ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of points equidistant from A and C.
Solution:
Question 8.
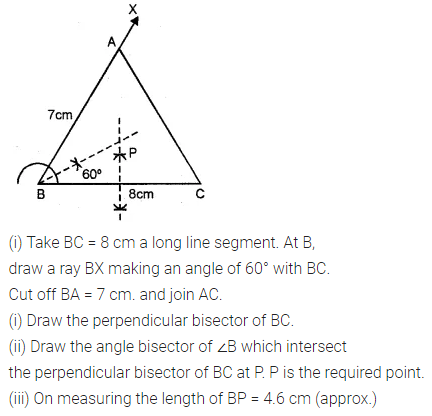
Construct triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
(i) P is equidistant from B and C and
(ii) P is equidistant from AB and BC
(iii) Measure and record the length of PB. (2000)
Solution:
Question 9.
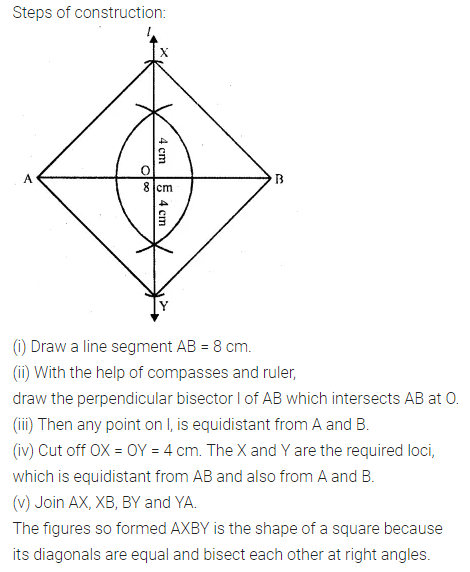
A straight line AB is 8 cm long. Locate by construction the locus of a point which is:
(i) Equidistant from A and B.
(ii) Always 4 cm from the line AB.
(iii) Mark two points X and Y, which are 4 cm from AB and equidistant from A and B. Name the figure AXBY.(2008)
Solution:
Question 10.
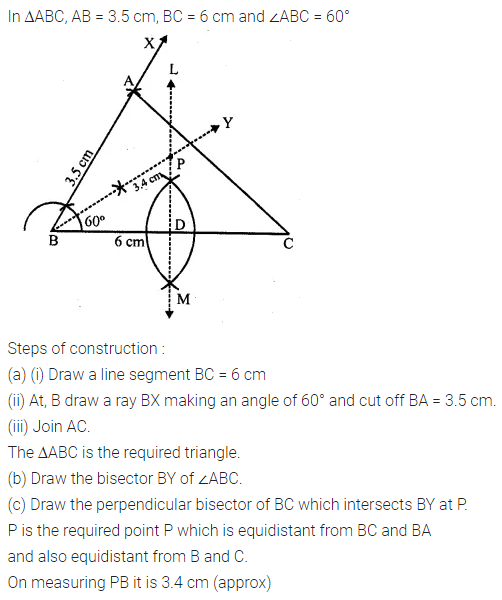
Use ruler and compasses only for this question.
(i) Construct ∆ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure arid record the length of PB. (2010)
Solution:
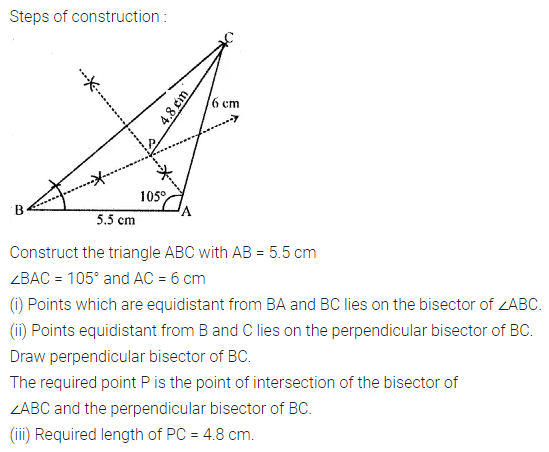
Question 11.
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°. Hence:
(i) Construct the locus of points equidistant from BA and BC.
(ii) Construct the locus of points equidistant from B and C.
(iii) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Solution:
Question 12.
In the given diagram, A, B and C are fixed collinear points; D is a fixed point outside the line: Locate

(i) the point P on AB such that CP = DP.
(ii) the points Q such that CQ = DQ = 3 cm. How many such points are possible?
(iii) the points R on AB such that DR = 4 cm. How many such points are possible?
(iv) the points S such that CS = DS and S is 4 cm away from the line CD. How many such points are possible?
(v) Are the points P, Q, R collinear?
(vi) Are the points P, Q, S collinear?
Solution:

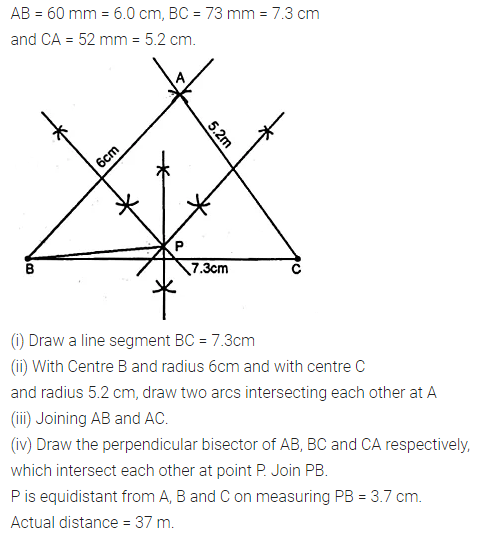
Question 13.
Points A, B and C represent the position of three towers such that AB = 60 m, BC = 73 m and CA = 52 m. Taking a scale of 10 m to 1 cm, make an accurate drawing of ∆ABC. Find by drawing, the location of a point which is equidistant from A, B and C, and its actual distance from any of the towers.
Solution:
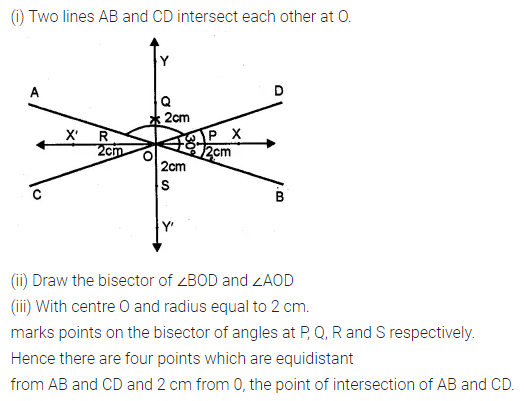
Question 14.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these lines and also 2 cm away from their point of intersection. How many such points exist? (1990)
Solution:
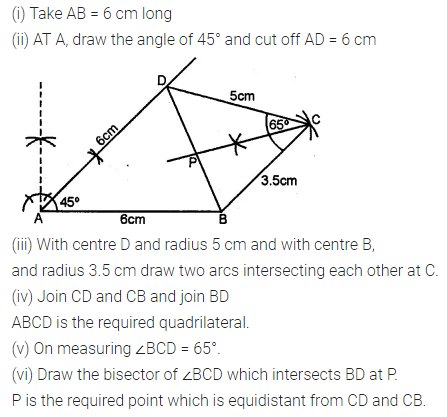
Question 15.
Without using set square or protractor, construct the quadrilateral ABCD in which ∠BAD = 45°, AD = AB = 6 cm, BC = 3.6 cm and CD = 5 cm.
(i) Measure ∠BCD.
(ii) Locate the point P on BD which is equidistant from BC and CD. (1992)
Solution:
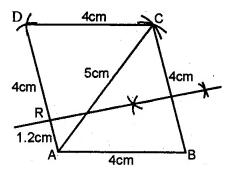
Question 16.
Without using set square or protractor, construct rhombus ABCD with sides of length 4 cm and diagonal AC of length 5 cm. Measure ∠ABC. Find the point R on AD such that RB = RC. Measure the length of AR. (1990)
Solution:

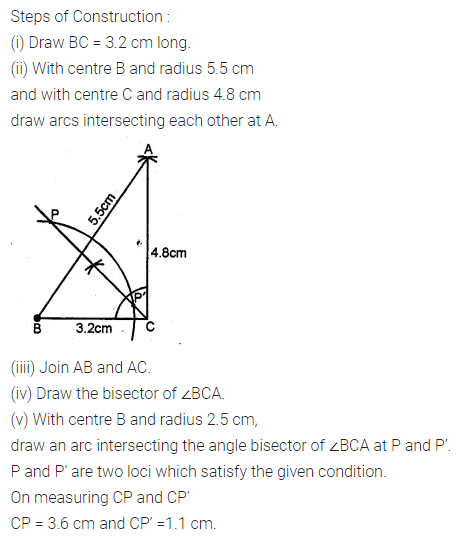
Question 17.
Without using set-squares or protractor construct :
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC. (1994)
Solution:
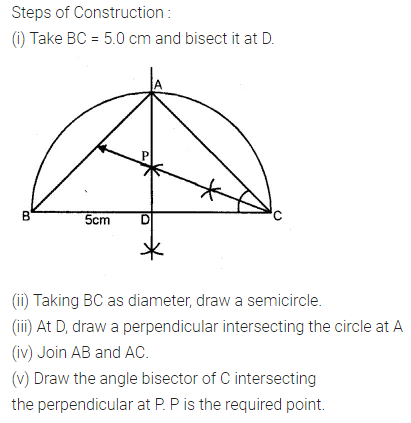
Question 18.
By using ruler and compasses only, construct an isosceles triangle ABC in which BC = 5 cm, AB = AC and ∠BAC = 90°. Locate the point P such that :
(i) P is equidistant from the sides BC and AC.
(ii) P is equidistant from the points B and C.
Solution:
Question 19.
Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6 cm, BC = 5 cm, ∠B = 60°, AD = 5 cm and D is equidistant from AB and BC. Measure CD. (1983)
Solution:

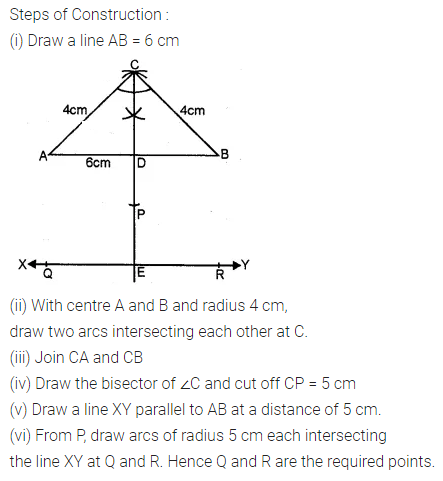
Question 20.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB (2001)
Solution:
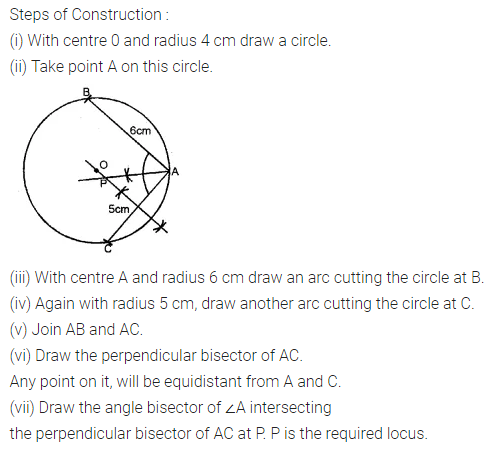
Question 21.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that is equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that is equidistant from AB and AC, (1995)
Solution:
Question 22.
Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
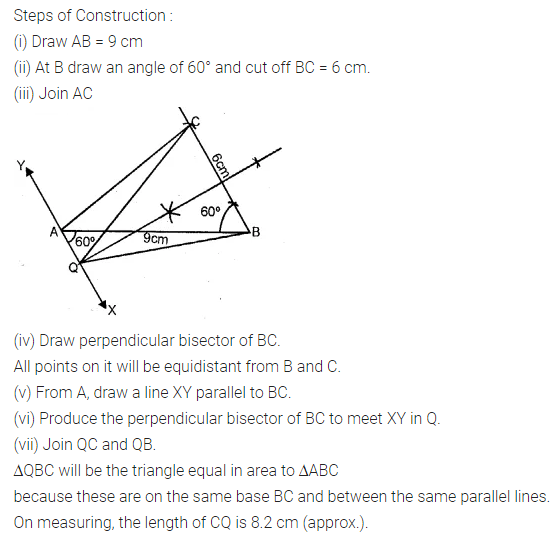
(i) Construct a triangle ABC, in which BC = 6 cm, AB = 9 cm. and ∠ABC = 60°.
(ii) Construct the locus of all points, inside ∆ABC, which are equidistant from B and C.
(iii) Construct the locus of the vertices of the triangles with BC as a base, which is equal in area to ∆ABC.
(iv) Mark the point Q, in your construction, which would make ∆QBC equal in area to ∆ABC, and isosceles.
(v) Measure and record the length of CQ. (1998)
Solution: