ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
Choose the correct answer from the given four options (1 to 13):
Question 1.
The slope of a line parallel to y-axis is
(a) 0
(b) 1
(c) -1
(d) not defined
Solution:
![]()
Question 2.
The slope of a line which makes an angle of 30° with the positive direction of x-axis is
(a) 1
(b) \(\frac { 1 }{ \sqrt { 3 } } \)
(c) √3
(d) \(– \frac { 1 }{ \sqrt { 3 } } \)
Solution:
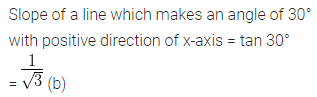
Question 3.
The slope of the line passing through the points (0, -4) and (-6, 2) is
(a) 0
(b) 1
(c) -1
(d) 6
Solution:
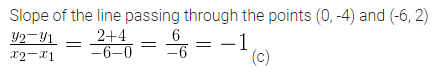
Question 4.
The slope of the line passing through the points (3, -2) and (-7, -2) is
(a) 0
(b) 1
(c) \(– \frac { 1 }{ 10 } \)
(d) not defined
Solution:
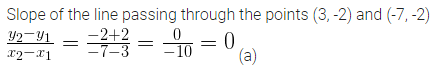
Question 5.
The slope of the line passing through the points (3, -2) and (3, -4) is
(a) -2
(b) 0
(c) 1
(d) not defined
Solution:
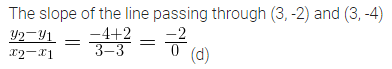
Question 6.
The inclination of the line y = √3x – 5 is
(a) 30°
(b) 60°
(c) 45°
(d) 0°
Solution:

Question 7.
If the slope of the line passing through the points (2, 5) and (k, 3) is 2, then the value of k is
(a) -2
(b) -1
(c) 1
(d) 2
Solution:
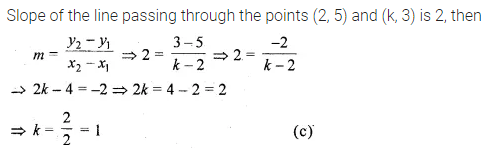
Question 8.
The slope of a line parallel to the line passing through the points (0, 6) and (7, 3) is
(a) \(– \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 5 } \)
(c) -5
(d) 5
Solution:
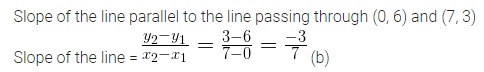
Question 9.
The slope of a line perpendicular to the line passing through the points (2, 5) and (-3, 6) is
(a) \(– \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 5 } \)
(c) -5
(d) 5
Solution:
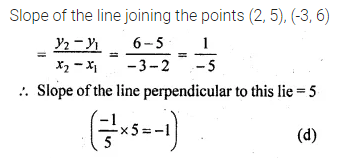
Question 10.
The slope of a line parallel to the line 2x + 3y – 7 = 0 is
(a) \(– \frac { 2 }{ 3 } \)
(b) \(\\ \frac { 2 }{ 3 } \)
(c) \(– \frac { 3 }{ 2 } \)
(d) \(\\ \frac { 3 }{ 2 } \)
Solution:
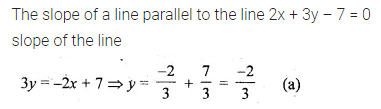
Question 11.
The slope of a line perpendicular to the line 3x = 4y + 11 is
(a) \(\\ \frac { 3 }{ 4 } \)
(b) \(– \frac { 3 }{ 4 } \)
(c) \(\\ \frac { 4 }{ 3 } \)
(d) \(– \frac { 4 }{ 3 } \)
Solution:

Question 12.
If the lines 2x + 3y = 5 and kx – 6y = 7 are parallel, then the value of k is
(a) 4
(b) -4
(c) \(\\ \frac { 1 }{ 4 } \)
(d) \(– \frac { 1 }{ 4 } \)
Solution:

Question 13.
If the line 3x – 4y + 7 = 0 and 2x + ky + 5 = 0 are perpendicular to each other, then the value of k is
(a) \(\\ \frac { 3 }{ 2 } \)
(b) \(– \frac { 3 }{ 2 } \)
(c) \(\\ \frac { 2 }{ 3 } \)
(d) \(– \frac { 2 }{ 3 } \)
Solution:
