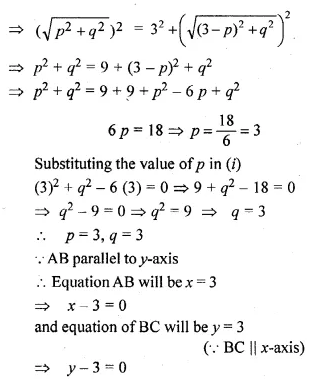ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2

Question 1.
State which one of the following is true:
The straight lines y = 3x – 5 and 2y = 4x + 7 are
(i) parallel
(ii) perpendicular
(iii) neither parallel nor perpendicular.
Solution:

Question 2.
If 6x + 5y – 7 = 0 and 2px + 5y + 1 = 0 are parallel lines, find the value of p.
Solution:

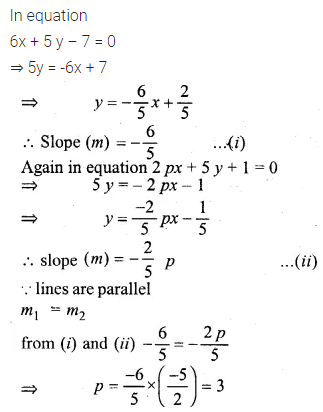
Question 3.
Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel. Find the relation connecting a and b. (1991)
Solution:

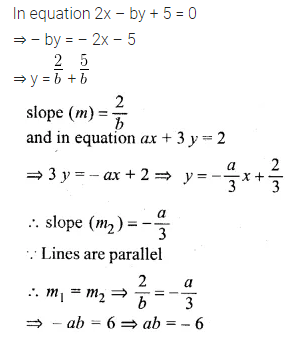
Question 4.
Given that the line \(\\ \frac { y }{ 2 } \) = x – p and the line ax + 5 = 3y are parallel, find the value of a. (1992)
Solution:

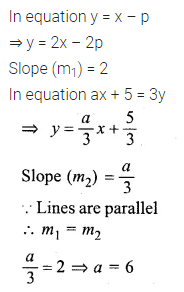
Question 5.
If the lines y = 3x + 7 and 2y + px = 3 perpendicular to each other, find the value of p. (2006)
Solution:

Question 6.
Find the value of k for which the lines kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other. (2003)
Solution:

Question 7.
If the lines 3x + by + 5 = 0 and ax – 5y + 7 = 0 are perpendicular to each other, find the relation connecting a and b.
Solution:

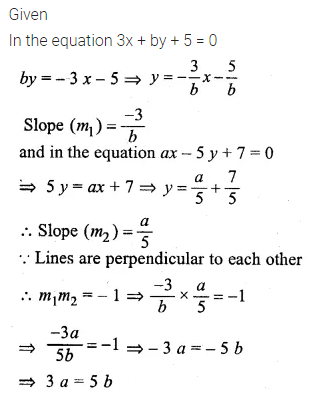
Question 8.
Is the line through (-2, 3) and (4, 1) perpendicular to the line 3x = y + 1 ?
Does the line 3x = y + 1 bisect the join of (-2, 3) and (4, 1). (1993)
Solution:

Question 9.
The line through A (-2, 3) and B (4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution:

Question 10.
If the lines 3x + y = 4, x – ay + 7 = 0 and bx + 2y + 5 = 0 form three consecutive sides of a rectangle, find the value of a and b.
Solution:

Question 11.
Find the equation of a line, which has the y-intercept 4, and is parallel to the line 2x – 3y – 7 = 0. Find the coordinates of the point where it cuts the x-axis. (1998)
Solution:

Question 12.
Find the equation of a straight line perpendicular to the line 2x + 5y + 7 = 0 and with y-intercept -3 units.
Solution:

Question 13.
Find the equation of a st. line perpendicular to the line 3x – 4y + 12 = 0 and having same y-intercept as 2x – y + 5 = 0.
Solution:

Question 14.
Find the equation of the line which is parallel to 3x – 2y = -4 and passes through the point (0, 3). (1990)
Solution:

Question 15.
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0. (1999)
Solution:

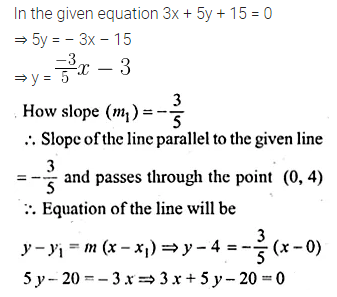
Question 16.
The equation of a line is y = 3x – 5. Write down the slope of this line and the intercept made by it on the y-axis. Hence or otherwise, write down the equation of a line which is parallel to the line and which passes through the point (0, 5).
Solution:

Question 17.
Write down the equation of the line perpendicular to 3x + 8y = 12 and passing through the point (-1, -2).
Solution:

Question 18.
(i) The line 4x – 3y + 12 = 0 meets the x-axis at A. Write down the co-ordinates of A.
(ii) Determine the equation of the line passing through A and perpendicular to 4x – 3y + 12 = 0. (1993)
Solution:

Question 19.
Find the equation of the line that is parallel to 2x + 5y – 7 = 0 and passes through the mid-point of the line segment joining the points (2, 7) and (-4, 1).
Solution:

Question 20.
Find the equation of the line that is perpendicular to 3x + 2y – 8 = 0 and passes through the mid-point of the line segment joining the points (5, -2), (2, 2).
Solution:

Question 21.
Find the equation of a straight line passing through the intersection of 2x + 5y – 4 = 0 with x-axis and parallel to the line 3x – 7y + 8 = 0.
Solution:

Question 22.
The equation of a line is 3x + 4y – 7 = 0. Find
(i) the slope of the line. .
(ii) the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0. (2010)
Solution:

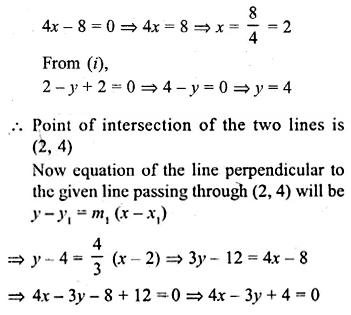
Question 23.
Find the equation of the line perpendicular from the point (1, -2) on the line 4x – 3y – 5 = 0. Also, find the co-ordinates of the foot of the perpendicular.
Solution:

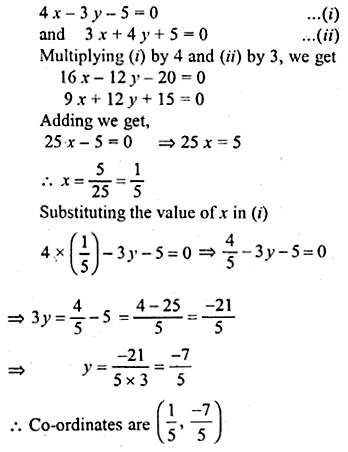
Question 24.
Prove that the line through (0, 0) and (2, 3) is parallel to the line through (2, -2) and (6, 4).
Solution:

Question 25.
Prove that the line through,(-2, 6) and (4, 8) is perpendicular to the line through (8, 12) and (4, 24).
Solution:

Question 26.
Show that the triangle formed by the points A (1, 3), B (3, -1) and C (-5, -5) is a right-angled triangle by using slopes.
Solution:

Question 27.
Find the equation of the line through the point (-1, 3) and parallel to the line joining the points (0, -2) and (4, 5).
Solution:

Question 28.
A (-1, 3), B (4, 2), C (3, -2) are the vertices of a triangle.
(i) Find the coordinates of the centroid G of the triangle.
(ii) Find the equation of the line through G and parallel to AC
Solution:

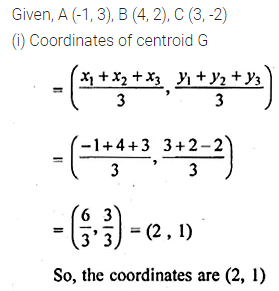
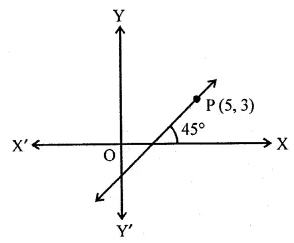
Question 29.
The line through P (5, 3) intersects y-axis at Q.
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the coordinates of Q.

Solution:

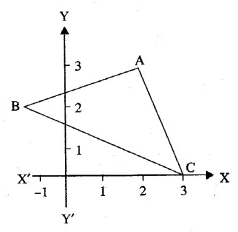
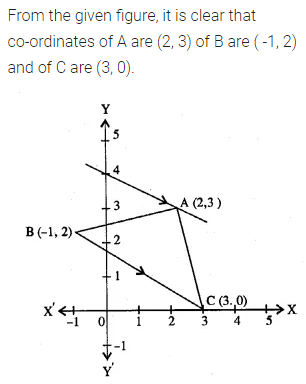
Question 30.
In the adjoining diagram, write down
(i) the co-ordinates of the points A, B and C.
(ii) the equation of the line through A parallel to BC. (2005)

Solution:

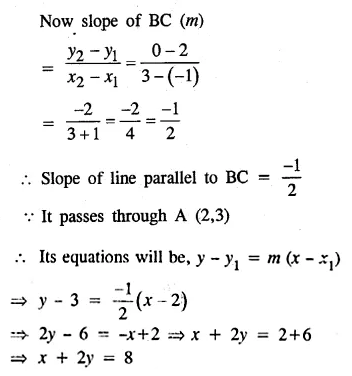
Question 31.
Find the equation of the line through (0, -3) and perpendicular to the line joining the points (-3, 2) and (9, 1).
Solution:

Question 32.
The vertices of a triangle are A (10, 4), B (4, -9) and C (-2, -1). Find the equation of the altitude through A. The perpendicular drawn from a vertex of a triangle to the opposite side is called altitude.
Solution:

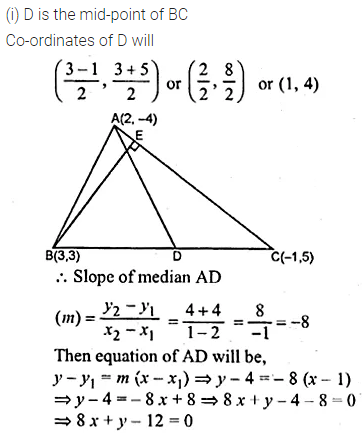
Question 33.
A (2, -4), B (3, 3) and C (-1, 5) are the vertices of triangle ABC. Find the equation of:
(i) the median of the triangle through A
(ii) the altitude of the triangle through B
Solution:

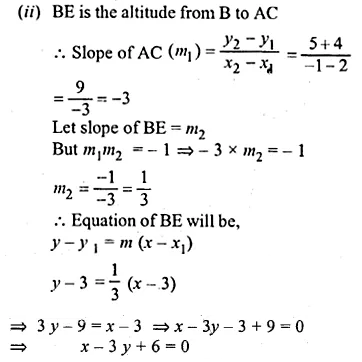
Question 34.
Find the equation of the right bisector of the line segment joining the points (1, 2) and (5, -6).
Solution:

Question 35.
Points A and B have coordinates (7, -3) and (1, 9) respectively. Find
(i) the slope of AB.
(ii) the equation of the perpendicular bisector of the line segment AB.
(iii) the value of ‘p’ if (-2, p) lies on it.
Solution:

Question 36.
The points B (1, 3) and D (6, 8) are two opposite vertices of a square ABCD. Find the equation of the diagonal AC.
Solution:

Question 37.
ABCD is a rhombus. The co-ordinates of A and C are (3, 6) and (-1, 2) respectively. Write down the equation of BD. (2000)
Solution:

Question 38.
Find the equation of the line passing through the intersection of the lines 4x + 3y = 1 and 5x + 4y = 2 and
(i) parallel to the line x + 2y – 5 = 0
(ii) perpendicular to the x-axis.
Solution:

Question 39.
(i) Write down the co-ordinates of the point P that divides the line joining A (-4, 1) and B (17, 10) in the ratio 1 : 2.
(ii) Calculate the distance OP where 0 is the origin
(iii) In what ratio does the y-axis divide the line AB?
Solution:

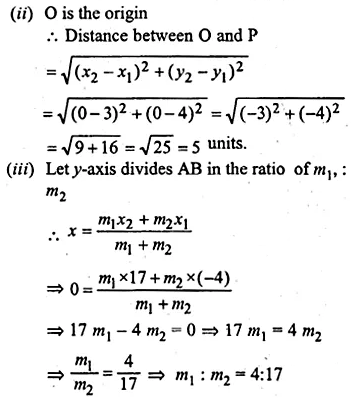
Question 40.
Find the image of the point (1, 2) in the line x – 2y – 7 = 0
Solution:

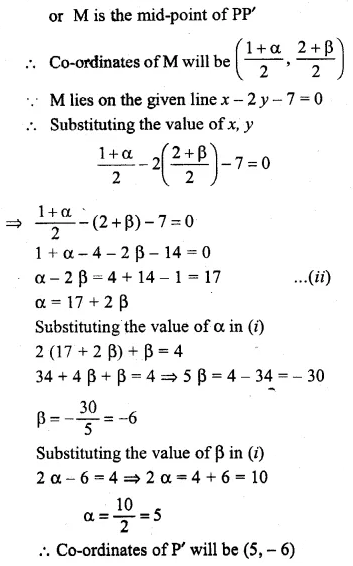
Question 41.
If the line x – 4y – 6 = 0 is the perpendicular bisector of the line segment PQ and the co-ordinates of P are (1, 3), find the co-ordinates of Q.
Solution:

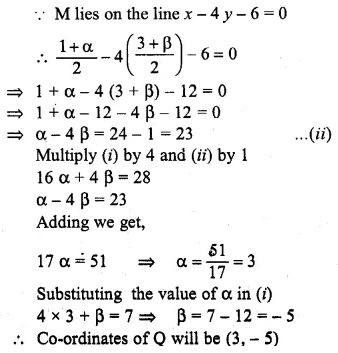
Question 42.
OABC is a square, O is the origin and the points A and B are (3, 0) and (p, q). If OABC lies in the first quadrant, find the values of p and q. Also, write down the equations of AB and BC.
Solution:

ML Aggarwal Class 10 Solutions for ICSE Maths