ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
Question 1.
Find the slope of a line whose inclination is
(i) 45°
(ii) 30°
Solution:
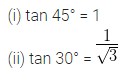
Question 2.
Find the inclination of a line whose gradient is
(i) 1
(ii) √3
(iii) \(\frac { 1 }{ \sqrt { 3 } } \)
Solution:
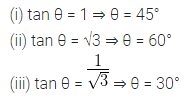
Question 3.
Find the equation of a straight line parallel 1 to x-axis which is at a distance
(i) 2 units above it
(ii) 3 units below it.
Solution:
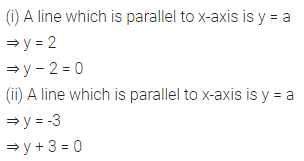
Question 4.
Find the equation of a straight line parallel to y-axis which is at a distance of:
(i) 3 units to the right
(ii) 2 units to the left.
Solution:

Question 5.
Find the equation of a straight line parallel to the y-axis and passing through the point (-3, 5).
Solution:

Question 6.
Find the equation of the a line whose
(i) slope = 3, y-intercept = -5
(ii) slope = \(– \frac { 2 }{ 7 } \), y-intercept = 3
(iii) gradient = √3, y-intercept = \(– \frac { 4 }{ 3 } \)
(iv) inclination = 30°, y-intercept = 2
Solution:
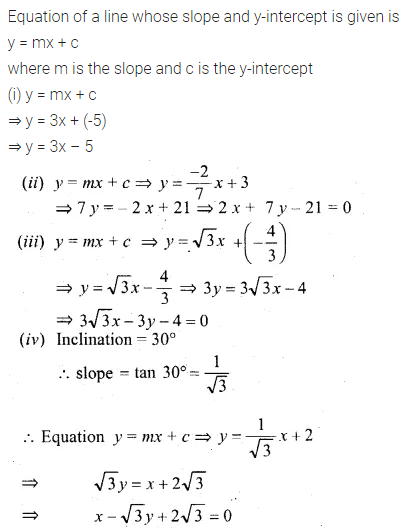
Question 7.
Find the slope and y-intercept of the following lines:
(i) x – 2y – 1 = 0
(ii) 4x – 5y – 9 = – 0
(iii) 3x +5y + 7 = 0
(iv) \(\frac { x }{ 3 } +\frac { y }{ 4 } =1\)
(v) y – 3 = 0
(vi) x – 3 = 0
Solution:

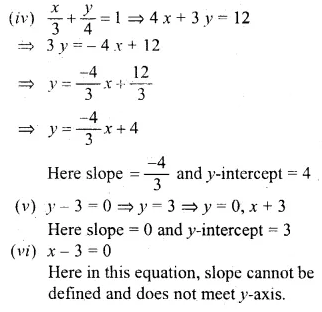
Question 8.
The equation of the line PQ is 3y – 3x + 7 = 0
(i) Write down the slope of the line PQ.
(ii) Calculate the angle that the line PQ makes with the positive direction of the x-axis.
Solution:

Question 9.
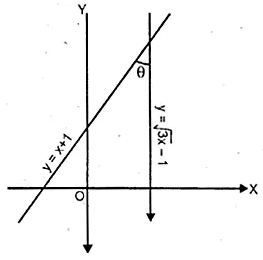
The given figure represents the line y = x + 1 and y = √3x – 1. Write down the angles which the lines make with the positive direction of the x-axis. Hence determine θ.
Solution:
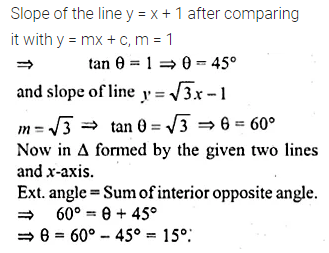
Question 10.
Find the value of p, given that the line \(\frac { y }{ 2 } =x-p\) passes through the point (-4, 4) (1992).
Solution:

Question 11.
Given that (a, 2a) lies on the line \(\frac { y }{ 2 } =3x-6\) find the value of a.
Solution:

Question 12.
The graph of the equation y = mx + c passes through the points (1, 4) and (-2, -5). Determine the values of m and c.
Solution:

Question 13.
Find the equation of the line passing through the point (2, -5) and making an intercept of -3 on the y-axis.
Solution:

Question 14.
Find the equation of a straight line passing through (-1, 2) and whose slope is \(\\ \frac { 2 }{ 5 } \).
Solution:
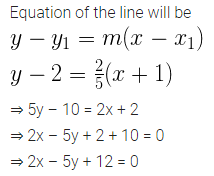
Question 15.
Find the equation of a straight line whose inclination is 60° and which passes through the point (0, -3).
Solution:

Question 16.
Find the gradient of a line passing through the following pairs of points.
(i) (0, -2), (3, 4)
(ii) (3, -7), (-1, 8)
Solution:

Question 17.
The coordinates of two points E and F are (0, 4) and (3, 7) respectively. Find:
(i) The gradient of EF
(ii) The equation of EF
(iii) The coordinates of the point where the line EF intersects the x-axis.
Solution:

Question 18.
Find the intercepts made by the line 2x – 3y + 12 = 0 on the co-ordinate axis.
Solution:
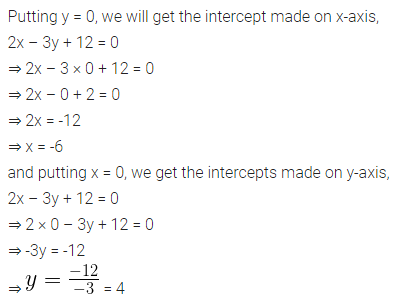
Question 19.
Find the equation of the line passing through the points P (5, 1) and Q (1, -1). Hence, show that the points P, Q and R (11, 4) are collinear.
Solution:
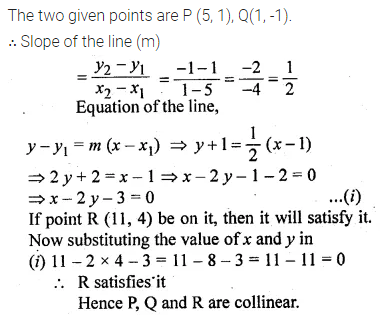
Question 20.
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line.
Solution:

Question 21.
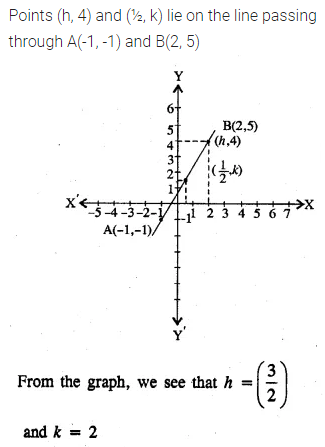
Use a graph paper for this question. The graph of a linear equation in x and y, passes through A (-1, -1) and B (2, 5). From your graph, find the values of h and k, if the line passes through (h, 4) and (½, k). (2005)
Solution:
Question 22.
ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, -4). Find
(i) the coordinates of A
(ii) the equation of the diagonal BD.
Solution:

Question 23.
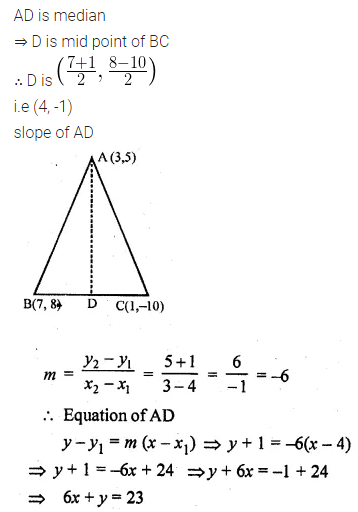
In ∆ABC, A (3, 5), B (7, 8) and C (1, -10). Find the equation of the median through A.
Solution:
Question 24.
Find the equation of a line passing through the point (-2, 3) and having x-intercept 4 units. (2002)
Solution:

Question 25.
Find the equation of the line whose x-intercept is 6 and y-intercept is -4.
Solution:

Question 26.
Write down the equation of the line whose gradient is \(\\ \frac { 1 }{ 2 } \) and which passes through P where P divides the line segment joining A (-2, 6) and B (3, -4) in the ratio 2 : 3. (2001)
Solution:

Question 27.
Find the equation of the line passing through the point (1, 4) and intersecting the line x – 2y – 11 = 0 on the y-axis.
Solution:

Question 28.
Find the equation of the straight line containing the point (3, 2) and making positive equal intercepts on axes.
Solution:

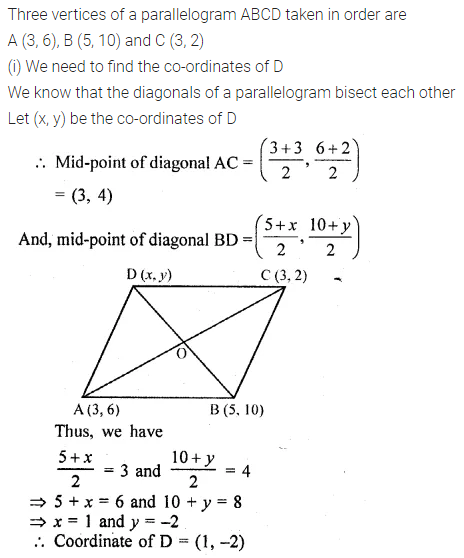
Question 29.
Three vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2) find:
(i) the coordinates of the fourth vertex D.
(ii) length of diagonal BD.
(iii) equation of side AB of the parallelogram ABCD. (2015)
Solution:

Question 30.
A and B are two points on the x-axis and y-axis respectively. P (2, -3) is the midpoint of AB. Find the
(i) the co-ordinates of A and B.
(ii) the slope of the line AB.
(iii) the equation of the line AB. (2010)
Solution:
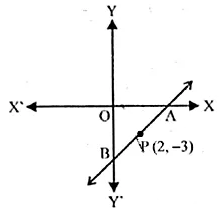

Question 31.
Find the equations of the diagonals of a rectangle whose sides are x = -1, x = 2 , y = -2 and y = 6.
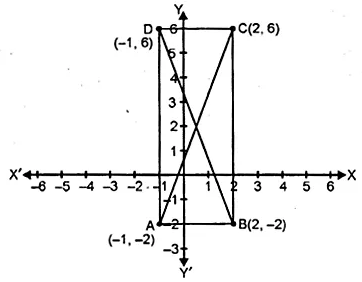
Solution:

Question 32.
Find the equation of a straight line passing through the origin and through the point of intersection of the lines 5x + 1y – 3 and 2x – 3y = 7
Solution:

Question 33.
Point A (3, -2) on reflection in the x-axis is mapped as A’ and point B on reflection in the y-axis is mapped onto B’ (-4, 3).
(i) Write down the co-ordinates of A’ and B.
(ii) Find the slope of the line A’B, hence find its inclination.
Solution:
