MCQ Questions for Class 9 Maths Chapter 9 Areas of Parallelogram and Triangles with Answers
MCQs from Class 9 Maths Chapter 9 – Areas of Parallelogram and Triangles are provided here to help students prepare for their upcoming Maths exam.
MCQs from CBSE Class 9 Maths Chapter 9: Areas of Parallelogram and Triangles
1) If ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 10 cm, AE = 6 cm and CF = 5 cm, then AD is equal to:
a. 10cm
B.6cm
c. 12cm
d. 15cm
Answer/ Explanation
Answer: (c)
Explanation: Given,
AB = CD = 10 cm (Opposite sides of a parallelogram)
CF = 5 cm and AE = 6 cm
Now,
Area of parallelogram = Base × Altitude
CD × AE = AD × CF
10 × 6 = AD × 5
AD = 60/5
AD = 12 cm
2) If E, F, G and H are the mid-points of the sides of a parallelogram ABCD, respectively, then ar (EFGH) is equal to:
a. 1/2 ar(ABCD)
b. ¼ ar(ABCD)
c. 2 ar(ABCD)
d. ar(ABCD)
Answer/ Explanation
Answer: (a)
Explanation: Join H and F as shown in the below figure:
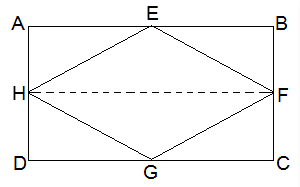
AD || BC and AD = BC
½ AD = ½ BC
AH || BF and and DH || CF
AH = BF and DH = CF (H and F are midpoints)
∴, ABFH and HFCD are parallelograms.
ΔEFH and llgmABFH, both lie on a common base, FH.
∴ area of EFH = ½ area of ABFH — 1
area of GHF = 1/2area of HFCD — 2
Adding eq. 1 and 2 we get;
area of ΔEFH + area of ΔGHF = ½ (area of ABFH + area of HFCD)
ar (EFGH) = ½ ar(ABCD)
3) If P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD, then:
a. ar(APB) > ar(BQC)
b. ar(APB) < ar(BQC)
c. ar(APB) = ar(BQC)
d. None of the above
Answer/ Explanation
Answer: (c)
Explanation: ΔAPB and parallelogram ABCD lie on the same base AB and in-between same parallel AB and DC.
ar(ΔAPB) = ½ ar(parallelogram ABCD) — 1
ar(ΔBQC) = ½ ar(parallelogram ABCD) — 2
From eq. 1 and 2:
ar(ΔAPB) = ar(ΔBQC)
4) If ABCD and EFGH are two parallelograms between same parallel lines and on the same base, then:
a. ar (ABCD) > ar (EFGH)
b. ar (ABCD) < ar (EFGH)
c. ar (ABCD) = ar (EFGH)
d. None of the above
Answer/ Explanation
Answer: (c)
5) A median of a triangle divides it into two
a. Congruent triangles
b. Isosceles triangles
c. Right triangles
d. Equal area triangles
Answer/ Explanation
Answer: (d)
Explanation: Suppose, ABC is a triangle and AD is the median.
AD is median of ΔABC.
∴ It will divide ΔABC into two triangles of equal area.
∴ ar(ABD) = ar(ACD) — (i)
also,
ED is the median of ΔABC.
∴ ar(EBD) = ar(ECD) — (ii)
Subtracting (ii) from (i),
ar(ABD) – ar(EBD) = ar(ACD) – ar(ECD)
⇒ ar(ABE) = ar(ACE)
6) In a triangle ABC, E is the mid-point of median AD. Then:
a. ar(BED) = 1/4 ar(ABC)
b. ar(BED) = ar(ABC)
c. ar(BED) = 1/2 ar(ABC)
d. ar(BED) = 2 ar(ABC)
Answer/ Explanation
Answer: (a)
Explanation: See the figure below:
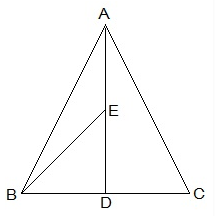
ar(BED) = ½ BD.DE
AE = DE (E is the midpoint)
BD = DC (AD is the median on side BC)
DE = ½ AD —- 1
BD = ½ BC —- 2
From eq. 1 and 2, we get;
ar(BED) = (½ ) x (½) BC x (½) AD
ar(BED) = (½) x (½) ar(ABC)
ar(BED) = ¼ ar (ABC)
7) If D and E are points on sides AB and AC respectively of ΔABC such that ar(DBC) = ar(EBC). Then:
a. DE is equal to BC
b. DE is parallel to BC
c. DE is not equal to BC
d. DE is perpendicular to BC
Answer/ Explanation
Answer: (b)
Explanation: ΔDBC and ΔEBC are on the same base BC and also having equal areas.
∴ they will lie between the same parallel lines.
∴ DE || BC.
8) If Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Then,
a. ar (AOD) = ar (BOC)
b. ar (AOD) > ar (BOC)
c. ar (AOD) < ar (BOC)
d. None of the above
Answer/ Explanation
Answer: (a)
Explanation: △DAC and △DBC lie on the same base DC and between the same parallels AB and CD.
ar(△DAC) = ar(△DBC)
⇒ ar(△DAC) − ar(△DOC) = ar(△DBC) − ar(△DOC)
⇒ ar(△AOD) = ar(△BOC)
9) If Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(△AOD) = ar(△BOC). Then ABCD is a:
a. Parallelogram
b. Rectangle
c. Square
d. Trapezium
Answer/ Explanation
Answer: (d)
Explanation: ar(△AOD) = ar(△BOC)
ar(△AOD) = ar(△BOC)
⇒ ar(△AOD) + ar(△AOB) = ar(△BOC) + ar(△AOB)
⇒ ar(△ADB) = ar(△ACB)
Areas of △ADB and △ACB are equal.
Therefore, they must lie between the same parallel lines.
Therefore, AB ∥ CD
Hence, ABCD is a trapezium.
10) If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram will be:
a. 1:2
b. 3:2
c. 1:4
d. 1:3
Answer/ Explanation
Answer: (a)
