MCQ Questions for Class 9 Maths Chapter 7 Triangles with Answers
MCQs from Class 9 Maths Chapter 7 – Triangles are provided here to help students prepare for their upcoming Maths exam.
MCQs from CBSE Class 9 Maths Chapter 7: Triangles
Q1. If E and F are the midpoints of equal sides AB and AC of a triangle ABC. Then:
a) BF=AC
b) BF=AF
c) CE=AB
d) BF = CE
Answer/Explanation
Answer: (d)
Explanation: AB and AC are equal sides.
AB = AC (Given)
∠A = ∠A (Common angle)
AE = AF (Halves of equal sides)
∆ ABF ≅ ∆ ACE (By SAS rule)
Hence, BF = CE (CPCT)
Q2. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Then:
a) BE>CF
b) BE<CF
c) BE=CF
d) None of the above
Answer/Explanation:
Answer: (c)
Explanation:
∠A = ∠A (common arm)
∠AEB = ∠AFC (Right angles)
AB = AC (Given)
∴ ΔAEB ≅ ΔAFC
Hence, BE = CF (by CPCT)
Q3. If ABC and DBC are two isosceles triangles on the same base BC. Then:
a) ∠ABD = ∠ACD
b) ∠ABD > ∠ACD
c) ∠ABD < ∠ACD
d) None of the above
Answer/Explanation
Answer: (a)
Explanation: AD = AD (Common arm)
AB = AC (Sides of isosceles triangle)
BD = CD (Sides of isosceles triangle)
So, ΔABD ≅ ΔACD.
∴ ∠ABD = ∠ACD (By CPCT)
Q4. If ABC is an equilateral triangle, then each angle equals to:
a) 90°
B)180°
c) 120°
d) 60°
Answer/Explanation
Answer: (d)
Explanation: Equilateral triangle has all its sides equal and each angle measures 60°.
AB= BC = AC (All sides are equal)
Hence, ∠A = ∠B = ∠C (Opposite angles of equal sides)
Also, we know that,
∠A + ∠B + ∠C = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
∴ ∠A = ∠B = ∠C = 60°
Q5. If AD is an altitude of an isosceles triangle ABC in which AB = AC. Then:
a) BD=CD
b) BD>CD
c) BD<CD
d) None of the above
Answer/Explanation
Answer: (c)
Explanation: In ΔABD and ΔACD,
∠ADB = ∠ADC = 90°
AB = AC (Given)
AD = AD (Common)
∴ ΔABD ≅ ΔACD (By RHS congruence condition)
BD = CD (By CPCT)
Q6. In a right triangle, the longest side is:
a) Perpendicular
b) Hypotenuse
c) Base
d) None of the above
Answer/Explanation
Answer: (b)
Explanation: In triangle ABC, right-angled at B.
∠B = 90
By angle sum property, we know:
∠A + ∠B + ∠C = 180
Hence, ∠A + ∠C = 90
So, ∠B is the largest angle.
Therefore, the side (hypotenuse) opposite to largest angle will be longest one.
Q7. In triangle ABC, if AB=BC and ∠B = 70, ∠A will be:
a) 70
b) 110
c) 55
d) 130
Answer
Answer: (c)
Explanation: Given,
AB = BC
Hence, ∠A=∠C
And ∠B = 70
By angle sum property of triangle we know:
∠A+∠B+∠C = 180
2∠A+∠B=180
2∠A = 180-∠B = 180-70 = 110
∠A = 55
Q8. For two triangles, if two angles and the included side of one triangle are equal to two angles and the included side of another triangle. Then the congruency rule is:
a) SSS
b) ASA
c) SAS
d) None of the above
Answer
(b)
Q9. A triangle in which two sides are equal is called:
a) Scalene triangle
b) Equilateral triangle
c) Isosceles triangle
d) None of the above
Answer
(c)
Q10. The angles opposite to equal sides of a triangle are:
a) Equal
b) Unequal
c) supplementary angles
d) Complementary angles
Answer
(a)
Q11. In two triangles DEF and PQR, if DE = QR, EF = PR and FD = PQ, then
a) ∆DEF ≅ ∆PQR
b) ∆FED ≅ ∆PRQ
c) ∆EDF ≅ ∆RPQ
d) ∆PQR ≅ ∆EFD
Answer
(b)
Q12. In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to:
a) 80o
b) 40o
c) 50o
d) 100o
Answer
(c)
Q13. Two sides of a triangle are of length 5 cm and 1.5 cm. The length of the third side of the triangle cannot be:
a) 3.6 cm
b) 4.1 cm
c) 3.8 cm
d) 6.9 cm
Answer
(d)
Q14. In ∆PQR, if ∠R > ∠Q, then
a) QR > PR
b) PQ > PR
c) PQ < PR
d) QR < PR
Answer
(b)
Q15. D is a point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
a) BD : DC = AB : AC
b) CD > CA
c) BD > BA
d) BA > BD
Answer
(a)
Q16. It is given that Δ ABC ≅ Δ FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
a) DF = 5 cm, ∠F = 60°
b) DF = 5 cm, ∠E = 60°
c) DE = 5 cm, ∠E = 60°
d) DE = 5 cm, ∠D = 40°
Answer
(b)
Q17. All the medians of a triangle are equal in case of a:
a) Scalene triangle
b) Right angled triangle
c) Equilateral triangle
d) Isosceles triangle
Answer
(c)
Q18. In the given figure, PS is the median then ∠QPS?
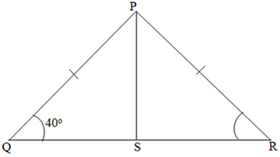
a) 40o
b) 50o
c) 80o
d) 90o
Answer
(b)
Q19. In triangle PQR if ∠Q = 90°, then:
a) PQ is the longest side
b) QR is the longest side
c) PR is the longest side
d) None of these
Answer
(c)
Q20. In the given figure, AB = AC and ∠B = 50° then; ∠A is:
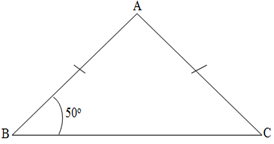
a) 50o
b) 80o
c) 100o
d) 130o
Answer
(b)
Q21. In the given figure, if the exterior angle is 135o then ∠P is:
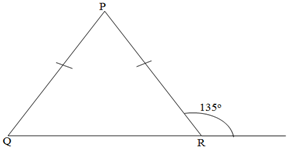
a) 45o
b) 60o
c) 80o
d) 90o
Answer
(d)
Q22. If in ΔPQR, PQ = PR then:
a) ∠P = ∠R
b) ∠P = ∠Q
c) ∠Q = ∠R
d) None of these
Answer
(c)
Q23. In a triangle ABC, ∠B = 35° and ∠C = 60°, then
a) ∠A = 80°
b) ∠A = 85°
c) ∠A = 120°
d) ∠A = 145°
Answer
(b)
Q24. In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are:
a) Isosceles but not congruent
b) Isosceles and congruent
c) Congruent but not isosceles
d) Neither congruent nor isosceles
Answer
(a)
Q25. In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if:
a) BC = EF
b) AC = DE
c) AC = EF
d) BC = DE
Answer
(b)
