MCQ Questions for Class 9 Maths Chapter 12 Heron’s with Answers
MCQs from Class 9 Maths Chapter 12 – Heron’s are provided here to help students prepare for their upcoming Maths exam.
MCQs from CBSE Class 9 Maths Chapter 12: Heron’s
1) Area of triangle is equal to:
a. Base x Height
b. 2(Base x Height)
c. ½(Base x Height)
d. ½ (Base + Height)
Answer/ Explanation
Answer: (c)
2) If the perimeter of a equilateral triangle is 180 cm. Then its area will be:
a. 900 cm2
b. 900√3 cm2
c. 300√3 cm2
d. 600√3 cm2
Answer/ Explanation
Answer: (b)
Explanation: Given, Perimeter = 180 cm
3a = 180 (Equilateral triangle)
a = 60 cm
Semi-perimeter = 180/2 = 90cm
Now as per Heron’s formula,
Hence, if we put the values here, we get:
A = 900√3
3) The sides of a triangle are 122 m, 22 m and 120 m respectively. The area of the triangle is:
a. 1320 sq.m
b. 1300 sq.m
c. 1400 sq.m
d. 1420 sq.m
Answer/ Explanation
Answer: (a)
Explanation: Given,
a = 122 m
b = 22 m
c = 120 m
Semi-perimeter, s = (122+22+120)/2 = 132 m
Using heron’s formula:
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)Put the values of s, a, b and c, to get the answer equal to 1320 sq.m.
4) The area of triangle with given two sides 18cm and 10cm respectively and perimeter equal to 42 cm is:
a. 20√11 cm2
b. 19√11 cm2
c. 22√11 cm2
d. 21√11 cm2
Answer/ Explanation
Answer: (d)
Explanation: Perimeter = 42
a+b+c=42
18+10+c=42
c=42-28=14 cm
Semiperimeter, s = 42/2 = 21cm
Using Heron’s formula:
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)Put the values of s, a, b and c, to get the answer equal to 21√11 cm2
5) The sides of a triangle are in the ratio 12 : 17 : 25 and its perimeter is 540cm. The area is:
a. 1000 sq.cm.
b. 5000 sq.cm.
c. 9000 sq.cm.
d. 8000 sq.cm.
Answer/ Explanation
Answer: (c)
Explanation:The ratio of the sides are 12:17:25
Perimeter = 540 cm
Let the sides of triangle be 12x, 17x and 25x.
Hence,
12x+17x+25x = 540 cm
54x = 540 cm
x = 10
Therefore,
a = 12x=12 x 10 = 120
b = 17x = 17 x 10 = 170
c = 25x = 25 x 10 = 250
Semi-perimeter, s = 540/2 = 270 cm
Putting the values of s, a, b and c in the Heron’s formula, we will get the area equal to 9000 sq.cm.
6) The equal sides of isosceles triangle are 12 cm and perimeter is 30 cm. The area of this triangle is:
a. 9√15 sq.cm
b. 6√15 sq.cm
c. 3√15 sq.cm
d. √15 sq.cm.
Answer/ Explanation
Answer: (a)
Explanation: Given,
Perimeter = 30cm
Semiperimeter, s = 30/2 = 15cm
a = b = 12cm
c=?
a+b+c = 30
12 +12+c=30
c=30-24 = 6cm
By putting the values of s, a, b and c in the Heron’s formula, we can get the value of area.
7) A quadrilateral whose sides are 3cm, 4cm, 4cm, 5cm and one of the diagonal is equal to 5cm as per the below figure. The area of the quadrilateral is:
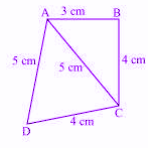
a. 19.17 sq.cm
b. 15.17 sq.cm
c. 20.17 sq.cm
d. 22.17 sq.cm.
Answer/ Explanation
Answer: (b)
Explanation: Using Pythagoras theorem, in ΔABC,
AC2 = AB2 + BC2
⇒ 52 = 32 + 42
⇒ 25 = 25
Hence, ABC is a right triangle.
Area of ΔABC = ½ x 3 x 4 = 6 sq.cm
Semiperimeter of ΔACD = (5+5+4)/2 = 14/2 = 7cm
Area of ΔACD can be determined by using Heron’s formula.
Therefore, the area of quad.ABCD = Area of ΔABC + Area of ΔACD
8) The area of an equilateral triangle having side length equal to √3/4cm is:
a. 2/27 sq.cm
b. 2/15 sq.cm
c. 3/16 sq.cm
d. 3/14 sq.cm
Answer/ Explanation
Answer: (c)
Explanation: Here, a = b = c = √3/4
Find the semi-perimeter of the triangle and use Heron’s formula to find the answer.
9) The sides of a parallelogram are 100 m each and length of the longest diagonal is 160m. The area of parallelogram is:
a. 9600 sq.m
b. 9000 sq.m
c. 9200 sq.m
d. 8800 sq.m
Answer/ Explanation
Answer: (a)
Explanation: The diagonal divides the parallelogram into two equivalent triangles. Hence, its area will be equal to the sum of area of the two triangles.
Hence, we can determine the area of the two triangles using Heron’s formula.
10) The sides of a triangle are in the ratio of 3 : 5 : 7 and its perimeter is 300 cm. Its area will be:
a. 1000√3 sq.cm
b. 1500√3 sq.cm
c. 1700√3 sq.cm
d. 1900√3 sq.cm
Answer/ Explanation
Answer: (b)
Explanation: Take the reference of Q.No.5
