Free PDF Download of CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Introduction to Trigonometry MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 8 Introduction to Trigonometry
1. The value of cos 0°. cos 1°. cos 2°. cos 3°… cos 89° cos 90° is
(a) 1
(b) -1
(c) 0
(d) \(\frac{1}{\sqrt{2}}\)
Answer
Answer: c
2. If x tan 45° sin 30° = cos 30° tan 30°, then x is equal to
(a) √3
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{\sqrt{2}}\)
(d) 1
Answer
Answer: d
3. If x and y are complementary angles, then
(a) sin x = sin y
(b) tan x = tan y
(c) cos x = cos y
(d) sec x = cosec y
Answer
Answer: d
4. sin 2B = 2 sin B is true when B is equal to
(a) 90°
(b) 60°
(c) 30°
(d) 0°
Answer
Answer: d
5. If A, B and C are interior angles of a ΔABC then \(\cos \left(\frac{\mathrm{B}+\mathrm{C}}{2}\right)\) is equal to

Answer
Answer: a
6. If A and (2A – 45°) are acute angles such that sin A = cos (2A – 45°), then tan A is equal to
(a) 0
(b) \(\frac{1}{\sqrt{3}}\)
(c) 1
(d) √3
Answer
Answer: c
7. If y sin 45° cos 45° = tan2 45° – cos2 30°, then y = …
(a) –\(\frac{1}{2}\)
(b) \(\frac{1}{2}\)
(c) -2
(d) 2
Answer
Answer: b
8. If sin θ + sin² θ = 1, then cos² θ + cos4 θ = ..
(a) -1
(b) 0
(c) 1
(d) 2
Answer
Answer: c
9. 5 tan² A – 5 sec² A + 1 is equal to
(a) 6
(6) -5
(c) 1
(d) -4
Answer
Answer: d
10. If sec A + tan A = x, then sec A =

Answer
Answer: d
11. If sec A + tan A = x, then tan A =

Answer
Answer: b
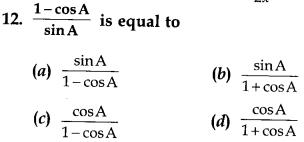
Answer
Answer: b
13. If x = a cos 0 and y = b sin 0, then b2x2 + a2y2 =
(a) ab
(b) b² + a²
(c) a²b²
(d) a4b4
Answer
Answer: c
14. What is the maximum value of \(\frac{1}{\csc A}\)?
(a) 0
(b) 1
(c) \(\frac{1}{2}\)
(d) 2
Answer
Answer: b
15. What is the minimum value of sin A, 0 ≤ A ≤ 90°
(a) -1
(b) 0
(c) 1
(d) \(\frac{1}{2}\)
Answer
Answer: b
16. What is the minimum value of cos θ, 0 ≤ θ ≤ 90°
(a) -1
(b) 0
(c) 1
(d) \(\frac{1}{2}\)
Answer
Answer: b
17. Given that sin θ = \(\frac{a}{b}\) , then tan θ =

Answer
Answer: c
18. If cos 9A = sin A and 9A < 90°, then the value of tan 5A is
(a) 0
(b) 1
(c) \(\frac{1}{\sqrt{3}}\)
(d) √3
Answer
Answer: b
19. If in ΔABC, ∠C = 90°, then sin (A + B) =
(a) 0
(b) 1/2
(c) \(\frac{1}{\sqrt{2}}\)
(d) 1
Answer
Answer: d
20. If sin A – cos A = 0, then the value of sin4 A + cos4 A is
(a) 2
(b) 1
(c) \(\frac{3}{4}\)
(d) \(\frac{1}{2}\)
Answer
Answer: d
21. Ratios of sides of a right triangle with respect to its acute angles are known as
(a) trigonometric identities
(b) trigonometry
(c) trigonometric ratios of the angles
(d) none of these
Answer/Explanation
Answer: c
Explaination: (c) trigonometric ratios of the angles
22. If tan θ = \(\frac{a}{b}\) then the value of
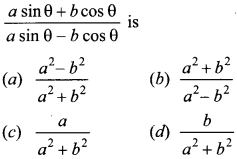
Answer/Explanation
Answer: b
Explaination:
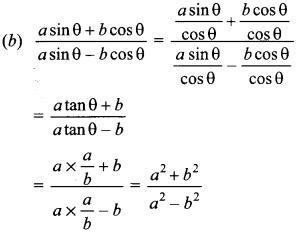
23. Match the Columns:

(a) 1 – A, 2 – C, 3 – B
(b) 1 – B, 2 – C, 3 – A
(c) 1 – B, 2 – C, 3 – D
(d) 1 – D, 2 – B, 3 – A
Answer/Explanation
Answer: b
Explaination:

24. In the given figure, if AB = 14 cm, then the value of tan B is:
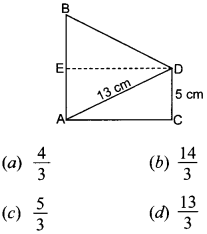
Answer/Explanation
Answer: a
Explaination:
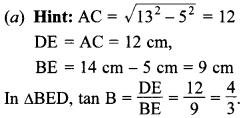
25. Match the Columns:

(a) 1 – A, 2 – C, 3 – B
(b) 1 – C, 2 – A, 3 – D
(c) 1 – B, 2 – A, 3 – E
(d) 1 – B, 2 – D, 3 – A
Answer/Explanation
Answer: d
Explaination: (d) definition of trigonometric ratios.
26. The value of sin² 30° – cos² 30° is
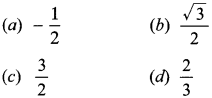
Answer/Explanation
Answer:
Explaination:

27. If 3 cot θ = 2, then the value of tan θ
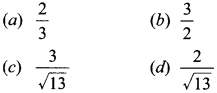
Answer/Explanation
Answer: b
Explaination:
3 cot θ = 2
⇒ cot θ \(\frac{2}{3}\)
tan θ = \(\frac{3}{2}\)
28. If ∆ABC is right angled at C, then the value of cos (A + B) is [NCERT Exemplar Problems]

Answer/Explanation
Answer: a
Explaination:
(a) ∆ ABC is right angled at C,
∴ A + B + C = 180°
A + B = 180° – 90° = 90° (∵ ∠C = 90°)
cos (A + B) = cos 90° = 0
29. If 0° < θ < 90°, then sec 0 is (a) >1
(b) < 1
(c) =1
(d) 0
Answer/Explanation
Answer: a
Explaination:
(a) ∵ sec θ = \(\frac{1}{\cos \theta}\)
∵ sce θ > 1.
30. If sin 0 = √3 cos θ, 0° < θ < 90°, then θ is equal to
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer/Explanation
Answer: c
Explaination:
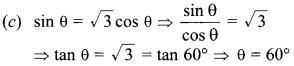
31. If cos (α + β) = 0, then sin (α – β) can be reduced to [NCERT Exemplar Problems]
(a) cos β
(b) cos 2β
(c) sin α
(d) sin 2α
Answer/Explanation
Answer: b
Explaination:
(b) cos (α + β) = 0 = cos 90°
⇒ α + β = 90°
sin (α – β) = sin (α – β + β – β)
= sin (α + β – 2β)
= sin (90° – 2β) = cos 2β
32. If cos 9α = sin a and 9α < 90°, then the value of tan 5α is [NCERT Exemplar Problems]
(a) \(\frac{1}{\sqrt{3}}\)
(b) √3
(c) 1
(d) 0
Answer/Explanation
Answer: c
Explaination:
cos 9α = sin α
⇒ cos 9α = cos (90° – α)
⇒ 9α = 90° – α
⇒ 10α = 90°
⇒ α = 9°
∴ tan 5α = tan 5 × 9°
= tan 45° = 1
33. sin (45° + θ) – cos (45° – θ) is equal to
(a) 2 cos θ
(b) 0
(c) 2 sin θ
(d) 1
Answer/Explanation
Answer: b
Explaination:
sin (45° + θ) – cos (45° – θ)
= sin {90° – (45° – θ)} – cos (45° – θ)
= cos (45° – θ) – cos (45° – θ) = 0
34. The value of sin² 5° + sin² 10° + sin² 15° + … + sin² 90° is equal to
(a) 8
(b) 8.5
(c) 9
(d) 9.5
Answer/Explanation
Answer: d
Explaination:
sin² 5° + sin² 10° + sin² 15° + ….. + sin² 90°
= (sin² 5° + sin² 85°) + (sin² 10° + sin² 80°) + … + (sin² 40° + sin² 50°) + sin² 45° + sin² 90°
= (sin² 5° + cos² 5°) + (sin 10° + cos² 10°) + … + (sin² 40° + cos² 40°) + \(\left(\frac{1}{\sqrt{2}}\right)^{2}\) + 1
= 1 + 1 + 1 + … 8 times + \(\frac{1}{2}\) + 1
= 9\(\frac{1}{2}\) = 9.5
35. The value of the expression [cosec (75° + θ) – sec (15° – θ) – tan (55° + θ) + cot (35° – θ)] is [NCERT Exemplar Problems]
(a) -1
(b) 0
(c) 1
(d) \(\frac{3}{2}\)
Answer/Explanation
Answer: b
Explaination:
cosec (75° + θ) – sec (15° – θ) – tan (55° + θ) + cot (35° – θ)
= cosec {90° – (15° – θ)} – sec (15° – θ) – tan {90° – (35° – θ)} + cot (35° – θ)
= sec (15° – θ) – sec (15° – θ) – cot (35° – θ) + cot (35° – θ) = 0
36. sin (90° – A) =
(a) sin A
(b) tan A
(c) cos A
(d) cosec A
Answer
Answer: c
37. tan A =
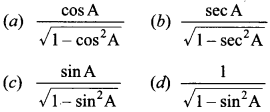
Answer/Explanation
Answer: c
Explaination:
![]()
38. If cosec A – cot A = —, then cosec A =
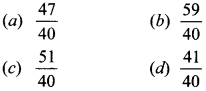
Answer/Explanation
Answer: d
Explaination:
cosec A – cot A = \(\frac{4}{5}\) ……(i)
Also cosec² A – cot² A = 1
⇒ (cosec A – cot A) (cosec A + cot A) = 1
⇒ \(\frac{4}{5}\)(cosec A + cot A) = 1
⇒ cosec A + cot A = \(\frac{4}{5}\) …(ii)
From (i) and (ii), cosec A = \(\frac{41}{40}\)
39. If sin x + cosec x = 2, then sin19x + cosec20x =
(a) 219
(b) 220
(c) 2
(d) 239
Answer/Explanation
Answer: c
Explaination:
(c) sin x + cosec x = 2
⇒ sin x + \(\frac{1}{sin x}\) = 2
⇒ sin² x + 1 = 2 sin x
⇒ (sin x – 1)² = 0 => sin x = 1 => cosec x = 1
∴ sin19 x + cosec20 x = 1 + 1 = 2
40. If sin θ – cos θ = 0, then the value of (sin4 θ + cos4 θ) is

Answer/Explanation
Answer: c
Explaination:
sin θ – cos θ = 0
⇒ (sin θ – cos θ)² = 0
⇒ sin2²θ + cos²θ – 2 sin θ cos θ = 0
⇒ – 2 sin θ cos θ = – 1
⇒ 2 sin θ cos θ=1
⇒ sin θ cos θ = \(\frac{1}{2}\)
⇒ sin²θ cos²θ = \(\frac{1}{4}\)
sin4θ + cos4θ = sin4θ + cos4θ + 2 sin²θ cos²θ – 2 sin²θ cos²θ
= (sin²θ + cos² θ)² – 2 sin²θ cos²θ
= (1)² – 2 × \(\frac{1}{4}\) = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
41. sec A =
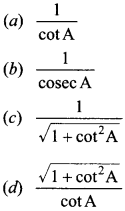
Answer/Explanation
Answer: d
Explaination:

42. 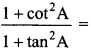
(a) tan² A
(b) sec² A
(c) cosec² A – 1
(d) 1 – sin² A
Answer/Explanation
Answer: c
Explaination:
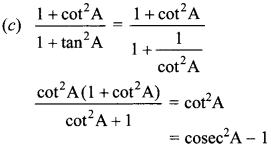
43. If sec A + tan A = x, then tan A =

Answer/Explanation
Answer: c
Explaination:
secA + tanA = x … (i)
Also sec² A – tan² A = 1
⇒ (sec A – tan A) (sec A + tan A) = 1
⇒ x (sec A – tan A)
∴ sec A – tan A = \(\frac{1}{x}\) ….. (ii)
Now, subtracting (ii) from (i), we have
tan A = \(\frac{x^{2}-1}{2 x}\)
44. Reciprocal of cot A is _____ .
Answer/Explanation
Answer:
Explaination: tan A
45. Reciprocal of cosec A is _____ .
Answer/Explanation
Answer:
Explaination: sin A
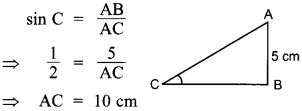
46. In ∆ABC, right angled at B, AB = 5 cm and sin C = \(\frac{1}{2}\). Determine the length of side AC.
Answer/Explanation
Answer:
Explaination:
47. If sec θ = \(\frac{25}{7}\), find the values of tan θ and cosec θ.
Answer/Explanation
Answer:
Explaination:

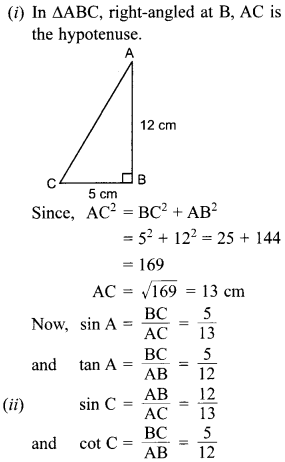
48. In ∆ABC, right angled at B, if AB = 12 cm and BC = 5 cm, find
(i) sin A and tan A, (ii) sin C and cot C.
Answer/Explanation
Answer:
Explaination:
49. If sin A = cos A, 0° < A < 90°, then A is equal to _____ .
Answer/Explanation
Answer:c
Explaination:
sin A = cos A sin A
⇒ \(\frac{\sin A}{\cos A}\) = 1
⇒ tan A = 1
⇒ A = 45°
50. If sin θ1 + sin θ2 + sin θ3 = 3, 0° < θ1 θ2, θ3 ≤ 90°, then cos θ1, + cos θ2, + cos θ3 = _____ .
Answer/Explanation
Answer:
Explaination:
Hint: Maximum value of sin 0 = 1
sin θ1 + sin θ2 + sin θ3 = 3
⇒ sin θ1 = 1, sin θ2 = 1 and sin θ3 = 1
⇒ θ1 = 90°, θ2 = 90° and θ3 = 90°
∴ cos θ1 + cos θ2 + cos θ3 = 0
51. Evaluate:
sin² 60° + 2 tan 45° – cos² 30° [Allahabad 2019]
Answer/Explanation
Answer:
Explaination:
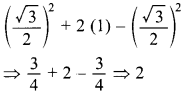
52. Given A = 30°, verify sin 2A = 2 sin A cos A.
Answer/Explanation
Answer:
Explaination:
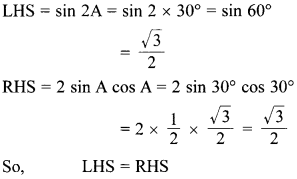
53. If tan θ = \(\frac{1}{\sqrt{3}}\) =r, then evaluate
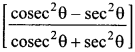
Answer/Explanation
Answer:
Explaination:
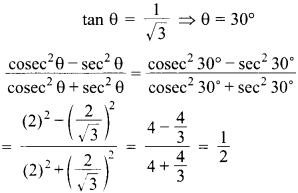
54. If sin (A – B) = \(\frac{1}{2}\), cos (A + B) = \(\frac{1}{2}\), find A and B.
Answer/Explanation
Answer:
Explaination:
sin (A – B) = \(\frac{1}{2}\)
⇒ A – B = 30° ……(i)
and cos (A + B) = \(\frac{1}{2}\)
⇒ A + B = 60 °…..(ii)
Solving equation (i) and (ii),
we get A = 45° and B = 15°
55. Value of \(\frac{\tan 65^{\circ}}{\cot 25^{\circ}}\) = _____.
Answer/Explanation
Answer:
Explaination:

56. If cos (40° + A) = sin 30°, the value of A is _____ .
Answer/Explanation
Answer:
Explaination:
Hint: cos (40° + A) = sin 30°
⇒ cos (40° + A) = cos (90° – 30°)
⇒ 40° + A = 60° => A = 20°
57. If tan θ = cot (30° + θ), find the value of θ.
Answer/Explanation
Answer:
Explaination:
tan θ = cot (30° + θ)
⇒ cot (90° – θ)
= cot (30° + θ)
⇒ 90° – θ = 30° + θ
⇒ 2θ = 60°
⇒ θ = 30°
58. Find the value of (sin²33° + sin²57°) [Delhi 2019]
Answer/Explanation
Answer:
Explaination:
sin²33° + sin²57°
⇒ sin²33° + sin²(90° – 33°)
⇒ sin²33° + cos²33° [Using sin(90° – θ) = cos θ]
⇒ 1 [Using sin²θ + cos² θ=1]
59. Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Answer/Explanation
Answer:
Explaination:
cot 85° + cos 75° = tan (90° – 85°) + sin (90° – 75°)
= tan 5° + sin 15°
60. If sec A = \(\frac{15}{7}\) and A + B = 90°, find the value of cosec B.
Answer/Explanation
Answer:
Explaination:
sec A = \(\frac{15}{7}\)
⇒ sec(90° – B) = \(\frac{15}{7}\) [∵ A + B = 90° ⇒ A = 90°-B]
⇒ cosec B = \(\frac{15}{7}\) [∵ sec (90° – θ) = cosec θ]
61. If tan A + cot A = 4, then tan4 A + cot4 A =
Answer/Explanation
Answer:
Explaination:
Hint: (tan A + cot A)2 = 42
⇒ tan² A + cot² A + 2 = 16
⇒ tan² A + cot² A = 14
⇒ (tan² A + cot² A)² = (14)²
⇒ tan4 A + cot4 A + 2 = 196
tan4 A + cot4 A = 194
62. If sin x + sin²x = 1, then value of cos² x + cos4 x
Answer/Explanation
Answer:
Explaination:
Hint: sin x + sin² x = 1
⇒ sin x = 1 – sin² x
⇒ sin x = cos² x
cos² x + cos4 x = cos² x (1 + cos² x)
= sin x (1 + sin x)
= sin x + sin² x = 1
63. If tan A = \(\frac{5}{12}\), find the value of 12 (sin A + cos A).sec A.
Answer/Explanation
Answer:c
Explaination:
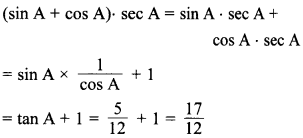
64. If cot θ = \(\frac{7}{8}\), evaluate
![]()
Answer/Explanation
Answer:
Explaination:
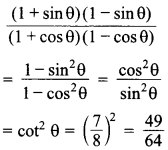
65. If sin θ = \(\frac{1}{3}\), then find the value of (2 cot² θ + 2)
Answer/Explanation
Answer:
Explaination:
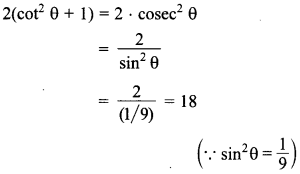
We hope the given MCQ Questions for Class 10 Maths Introduction to Trigonometry with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.