Free PDF Download of CBSE Class 10 Maths Chapter 7 Coordinate Geometry Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Coordinate Geometry MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 7 Coordinate Geometry
1. The distance of the point P(2, 3) from the x-axis is
(a) 2
(b) 3
(c) 1
(d) 5
Answer/ Explanation
Answer: b
Explaination: Reason: The distance from x-axis is equal to its ordinate i.e., 3
2. The distance between the point P(1, 4) and Q(4, 0) is
(a) 4
(b) 5
(c) 6
(d) 3√3
Answer/ Explanation
Answer: b
Explaination: Reason: The required distance = \(\sqrt{(4-1)^{2}+(0-4)^{2}}=\sqrt{9+16}=\sqrt{25}=5\)
3. The points (-5, 1), (1, p) and (4, -2) are collinear if
the value of p is
(a) 3
(b) 2
(c) 1
(d) -1
Answer/ Explanation
Answer: d
Explaination: Reason: The points are collinear if area of Δ = 0
= \(\frac{1}{2}\)[-5(p + 2) +l(-2 -1) + 4(1 – p)] – 0
⇒ -5 p -10-3 + 4-4p = 0
⇒ -9p = +9
∴ p = -1
4. The area of the triangle ABC with the vertices A(-5, 7), B(-4, -5) and C(4, 5) is
(a) 63
(b) 35
(c) 53
(d) 36
Answer/ Explanation
Answer: c
Explaination: Reason: Area of ΔABC = \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= \(\frac{1}{2}\)[-5(-5 – 5) -4(5 – 7) + 4(7 – (-5))] = \(\frac{1}{2}\)[-5(-10) -4(-2) + 4(12)]
= \(\frac{1}{2}\)[50 + 8 + 48] = \(\frac{1}{2}\) × 106 = 53 sq. units
5. The distance of the point (α, β) from the origin is
(a) α + β
(b) α² + β²
(c) |α| + |β|
(d) \(\sqrt{\alpha^{2}+\beta^{2}}\)
Answer/ Explanation
Answer: d
Explaination: Reason: Distance of (α, β) from origin (0, 0) = \(\sqrt{(\alpha-0)^{2}+(\beta-0)^{2}}=\sqrt{\alpha^{2}+\beta^{2}}\)
6. The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is
(a) 11
(b) 22
(c) 33
(d) 21
Answer/ Explanation
Answer: a
Explaination: Reason: Required area= \(\frac{1}{2}\)[1(3 + 4) -2(-4 – 2) -3(2 – 3)]
= \(\frac{1}{2}\)[7 + 12 + 3]
= \(\frac{1}{2}\) × 22 = 11
7. The line segment joining the points (3, -1) and (-6, 5) is trisected. The coordinates of point of trisection are
(a) (3, 3)
(b) (- 3, 3)
(c) (3, – 3)
(d) (-3,-3)
Answer/ Explanation
Answer: b
Explaination: Reason: Since the line segment AB is trisected

8. The line 3x + y – 9 = 0 divides the line joining the points (1, 3) and (2, 7) internally in the ratio
(a) 3 : 4
(b) 3 : 2
(c) 2 : 3
(d) 4 : 3
Answer/ Explanation
Answer: a
Explaination: Reason: Let the line 3x + y – 9 = 0 divide the line segment joining A(l, 3) ad B(2, 7) in the ratio K : 1 at point C.

9. The distance between A (a + b, a – b) and B(a – b, -a – b) is
Answer/ Explanation
Answer: c
Explaination:
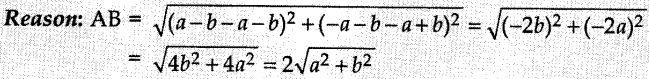
10. If (a/3, 4) is the mid-point of the segment joining the points P(-6, 5) and R(-2, 3), then the value of ‘a’ is
(a) 12
(b) -6
(c) -12
(d) -4
Answer/ Explanation
Answer: c
Explaination:

11. If the distance between the points (x, -1) and (3, 2) is 5, then the value of x is
(a) -7 or -1
(b) -7 or 1
(c) 7 or 1
(d) 7 or -1
Answer/ Explanation
Answer: d
Explaination: Reason: We have \(\sqrt{(x-3)^{2}+(-1-2)^{2}}=5\)
⇒ (x – 3)² + 9 = 25
⇒ x² – 6x + 9 + 9 = 25
⇒ x² -6x – 7 = 0
⇒ (x – 7)(x + 1) = 0
⇒ x = 7 or x = -1
12. The points (1,1), (-2, 7) and (3, -3) are
(a) vertices of an equilateral triangle
(b) collinear
(c) vertices of an isosceles triangle
(d) none of these
Answer/ Explanation
Answer: b
Explaination: Reason: Let A(1, 1), B(-2, 7) and C(3, 3) are the given points, Then, we have

13. The coordinates of the centroid of a triangle whose vertices are (0, 6), (8,12) and (8, 0) is
(a) (4, 6)
(b) (16, 6)
(c) (8, 6)
(d) (16/3, 6)
Answer/ Explanation
Answer: d
Explaination: Reason: The co-ordinates of the centroid of the triangle is

14. Two vertices of a triangle are (3, – 5) and (- 7,4). If its centroid is (2, -1), then the third vertex is
(a) (10, 2)
(b) (-10,2)
(c) (10,-2)
(d) (-10,-2)
Answer/ Explanation
Answer: c
Explaination: Reason: Let the coordinates of the third vertex be (x, y)
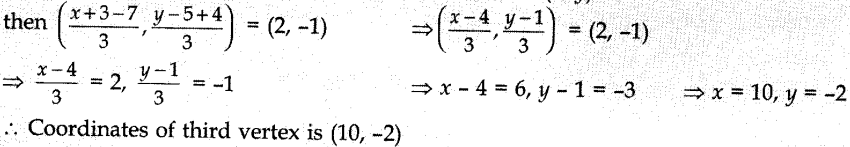
15. The area of the triangle formed by the points A(-1.5, 3), B(6, -2) and C(-3, 4) is
(a) 0
(b) 1
(c) 2
(d) 3/2
Answer/ Explanation
Answer: a
Explaination: Reason: Area of ΔABC = \(\frac{1}{2}\) [-1.5(-2 – 4) + 6(4 – 3) + (-3) (3 + 2)] = \(\frac{1}{2}\) [9 + 6 – 15] = 0. It is a straight line.
16. If the points P(1, 2), B(0, 0) and C(a, b) are collinear, then
(a) 2a = b
(b) a = -b
(c) a = 2b
(d) a = b
Answer/ Explanation
Answer: a
Explaination: Reason: Area of ΔPBC = 0
⇒ \(\frac{1}{2}\)[1(0 – b) + 0(6 – 1) + a(2 – 0)] = 0
⇒ \(\frac{1}{2}\)[-6 + 2a] = 0
⇒ -b + 2a = 0
∴ 2a = b
17. A triangle with vertices (4, 0), (- 1, – 1) and (3, 5) is a/an
(a) equilateral triangle
(b) right-angled triangle
(c) isosceles right-angled triangle
(d) none of these
Answer/Explanation
Answer: a
Explaination:

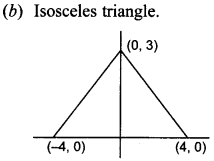
18. The points (- 4, 0), (4, 0) and (0, 3) are the vertices of a/an [NCERT Exemplar Problems]
(a) right triangle
(b) isosceles triangle
(c) equilateral triangle
(d) scalene triangle
Answer/Explanation
Answer: b
Explaination:
19. A circle drawn with origin as the centre passes through , \(\left(\frac{13}{2}, 0\right)\). The point which does not lie in the interior of the circle is [NCERT Exemplar Problems]
Answer/Explanation
Answer: d
Explaination:

20. If the distance between the points(4, p) and (1, 0) is 5 units, then the value of p is [NCERT Exemplar Problems]
(a) 4 only
(b) ± 4
(c) -4 only
(d) 0
Answer/Explanation
Answer: b
Explaination:

21. The points (2, 5), (4, – 1) and (6, – 7) are vertices of an/a
(a) isosceles triangle
(b) equilateral triangle
(c) right-angled triangle
(d) none of these
Answer/Explanation
Answer: d
Explaination:
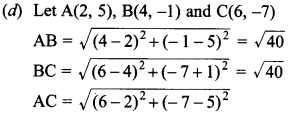
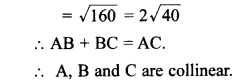
22. If the segment joining the points (a, b) and (c, d) subtends a right angle at the origin, then
(a) ac – bd = 0
(b) ac + bd = 0
(c) ab + cd = 0
(d) ab – cd= 0
Answer/Explanation
Answer: b
Explaination:
Let A {a, b), B(c, d), 0(0, 0)
∴ ∠AOB = 90°
⇒ AB² = AO² + BO²
(c – a)² + (d- b)² = a² + b² + c² + d²
⇒ ac + bd = 0
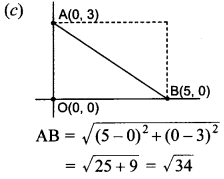
23. AOBC is a rectangle whose three vertices are A(0, 3), 0(0, 0) and B(5, 0). The length of its diagonal is [NCERT Exemplar Problems]
(a) 5
(b) 3
(c) √34
(d) 4
Answer/Explanation
Answer: c
Explaination:
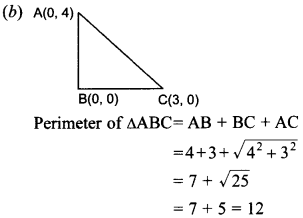
24. The perimeter of a triangle with vertices (0,4), (0, 0) and (3, 0) is [NCERT Exemplar Problems]
(a) 5
(b) 12
(c) 11
(d) 7 + √5
Answer/Explanation
Answer: b
Explaination:
 `
`
25. If the distance between the points (4, p) and (1, 0) is 5 units, then the value of p is [NCERT Exemplar Problems]
(a) 4 only
(b) ±4
(c) -4 only
(d) 0
Answer/Explanation
Answer: b
Explaination:
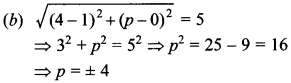
26. If p\(\left(\frac{a}{3}, 4\right)\) is the mid-point of the line segment joining the points Q (-6, 5) and R (-2, 3), then the value of a is [NCERT Exemplar Problems]
(a) -4
(b) -12
(c) 12
(d) -6
Answer/Explanation
Answer: b
Explaination:
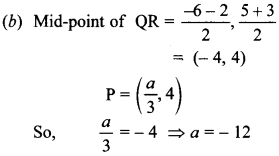
27. If P(l, 2), Q(4, 6), R(5, 7) and S(a, b) are the vertices of a parallelogram PQRS, then
(a) a = 2,b = A
(b) a = 3,b = 4
(c) a = 2, b = 3
(d) a = 3, b = 5
Answer/Explanation
Answer: c
Explaination:

28. The point P which divides the line segment joining the points A(2, -5) and B(5, 2) in the ratio 2 : 3 lies in the quadrant
(a) I
(b) II
(c) III
(d) IV
Answer/Explanation
Answer: d
Explaination:|

29. The points (k + 1, 1), (2k + 1, 3) and (2k + 2, 2k) are collinear if
(a) k = -1, 2
(b) k=\(\frac{1}{2}\),2
(c) k = 2, 1
(d) k = –\(\frac{1}{2}\),2
Answer/Explanation
Answer: d
Explaination:
∵ Points are collinear.
∴ (k + 1) (3 – 2k) + (2k + 1) (2k- 1) + (2k + 2) (1 – 3) = 0
⇒ 3k + 3 – 2k² – 2k + 4k² – 1 -4k – 4 = 0
⇒ 2k² – 3k – 2 = 0
⇒ 2k² – 4k + k – 2 = 0
⇒ 2k(k – 2) + 1(k – 2) = 0
⇒ (2k + 1) (k – 2) = 0
k = –\(\frac{1}{2}\), k = 2
30. The area of the triangle with vertices at the points (a, b + c), (b, c + a) and (c, a + b) is
(a) (a + b + c) sq. units
(b) (a + b – c) sq. units
(c) (a – b + cj sq. units
(d) 0
Answer/Explanation
Answer: d
Explaination:
Using formula for area of triangle, we get
Area = zero.
Area of triangle
= \(\frac{1}{2}\)| a(c + a- a-b) + b(a+ b- b-c) + c(b + c- c-a) |
= \(\frac{1}{2}\) |ac – ab + ba – bc + cb – ca| = 0
31. The area (in square units) of the triangle formed by the points A(a, 0), 0(0, 0) and B(0, b) is

Answer/Explanation
Answer: b
Explaination:
A (a, 0), O(0, 0) and B(0, b)
ar(∆AOB) = \(\frac{1}{2}\)|a(0 – b) + 0(b – 0) + 0(0 -0)|
= \(\frac{1}{2}\)|-ab + 0 + 0| = \(\frac{ab}{2}\)
32. The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is [NCERT Exemplar Problems]

Answer/Explanation
Answer: a
Explaination:
∵ AOB is a right triangle.
∴ Mid-point of AB is equidistant from A, O and B.
33. The vertices of a triangle are (0, 0), (3, 0) and (0, 4). The centroid of the triangle is

Answer/Explanation
Answer: b
Explaination:
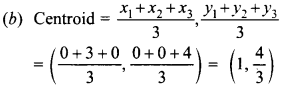
34. If A = (a , 2a) and B = \(\left(\frac{1}{a^{2}},-\frac{2}{a}\right)\) S = (1,0), then \(\frac{1}{\mathrm{SA}}+\frac{1}{\mathrm{SB}}=\) = _______ .
Answer/Explanation
Answer:
Explaination:
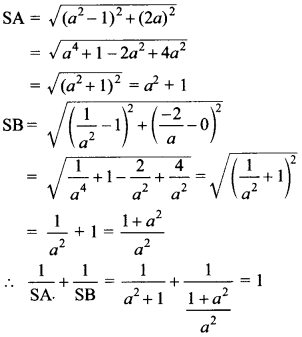
35. Find the distance of a point P(x, y) from the origin. [CBSE 2018]
Answer/Explanation
Answer:
Explaination:

36. Find the distance between the points \(\left(-\frac{8}{5}, 2\right) \text { and }\left(\frac{2}{5}, 2\right)\)
Answer/Explanation
Answer:
Explaination:
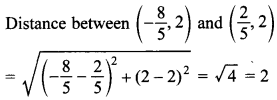
37. If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k? [Delhi 2017]
Answer/Explanation
Answer:
Explaination:

38. Show that (1, -1) is the centre of the circle circumscribing the triangle whose angular points are (4, 3), (- 2, 3) and (6, – 1).
Answer/Explanation
Answer:
Explaination:

39. A circle has its centre at the origin and a point P(5, 0) lies on it. The point Q(6, 8) lies outside the circle. State whether true or false. Justify your answer. [NCERT Exemplar Problems]
Answer/Explanation
Answer:
Explaination:
True, because distance between centre (origin) and Q(6,8) is greater than its radius, i.e. 5.
40. Find the coordinates of a point A, where AB is diameter of a circle whose centre is (2, -3) and B is the point (1, 4).
[Delhi 2019]
Answer/Explanation
Answer:
Explaination:
AB is diameter of the circle.
Let C be centre of circle, coordinates of C are (2, -3). So, C is mid-point of AB (diameter).
Let coordinates of A are (x, y).
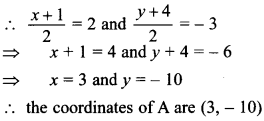
41. A straight line is drawn joining the points (3, 4) and (5, 6). If the line is extended, the ordinate of the point on the line, whose abscissa is -1 is ________ .
Answer/Explanation
Answer:
Explaination:

42. In figure, P(5, -3) and Q(3,y) are the points of trisection of the line segment joining A(7, -2) and B (1, -5). Then y equals ________ .
![]()
Answer/Explanation
Answer:
Explaination:

43. A(5, 1); B(l, 5) and C(-3, – 1) are the vertices of ∆ABC. Find the length of median AD. [CBSE 2018 (C)]
Answer/Explanation
Answer:
Explaination:
AD is median of ΔABC
∴ D is mid-point of BC
Coordinates of

44. If the mid-point of the line segment joining the points P(6, b – 2) and Q(- 2, 4) is (2, – 3), find the value of b.
Answer/Explanation
Answer:
Explaination:

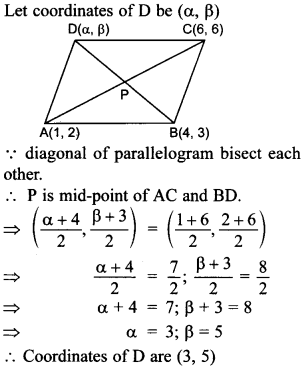
45. If A(1, 2), B(4, 3) and C(6, 6) are the three vertices of a parallelogram ABCD, find the coordinates of the fourth vertex D.
Answer/Explanation
Answer:
Explaination:
46. Find the coordinates of the centroid of a triangle whose vertices are (0, 6), (8, 12) and (8, 0).
Answer/Explanation
Answer:
Explaination:

47. Two vertices of a triangle are (3, -5) and (-7, 4). If its centroid is (2, – 1), find the third vertex.
Answer/Explanation
Answer:
Explaination:

48. The coordinates of one end point of a diameter of a circle are (4, -1) and the coordinates of the centre are (1, -3). Find the coordinates of the other end of the diameter.
Answer/Explanation
Answer:
Explaination:
![]()
Given that coordinates of one end point of the diameter is (4, -1) and centre of the circle is (1, – 3).
Let coordinates of the other end of the diameter be (x, y).
We know that the centre of the circle (1, -3) is the mid-point of diameter.
⇒ \(\frac{4+x}{2}\) = 1 and \(\frac{(-1+y)}{2}\) ,
⇒ 4 + x = 2 and -1 + y = -6
⇒ x = – 2 and y = -6 + 1 = -5
Thus, coordinates of the other end of the diameter are (-2, -5).
49. Point P divides the line segment joining the points A(2, -5) and B(5, 2) in the ratio 2:3. Name the quadrant in which P lies. [Delhi 2011]
Answer/Explanation
Answer:
Explaination:

50. In figure, P(5, -3) and Q(3, vj are the points of trisection of the line segment joining A(7, -2) and B(1, -5). Find y [Foreign 2013]
Answer/Explanation
Answer:
Explaination:
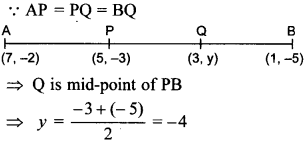
51. Area of the triangle formed by (1, – 4), (3, – 2) and (- 3, 16) is _______ .
Answer/Explanation
Answer:
Explaination:
Area of the ∆ = \(\frac{1}{2}\)|1(-2 – 16) + 3(16 + 4) + (-3) (-4 + 2)|
= \(\frac{1}{2}\)| -18 + 60 + 6 | = 24 sq. units
52. If the points (- 2, – 5), (2, – 2) and (8, p) are collinear, then the value of p is _______ .
Answer/Explanation
Answer:
Explaination:
Points are collinear
∴ x1y2 + x2y3 + x3y1 – x2y1– x3y2 – x1y3 = 0
⇒ (-2) × (-2) + (2) × (p) + 8 × (-5) – (2) × (-5) – (8) × (-2) – (-2) ×(p) = 0
⇒ 4 + 2p – 40 + 10 + 16 + 2p = 0
⇒ 4p – 40 + 30 = 0
⇒ 4p = 10 10 5
⇒ p = \(\frac{10}{4}\) = \(\frac{5}{2}\)/
53. Show that the points P(\(\frac{-3}{2}\), 3), Q(6, -2) and R(-3, 4) are collinear.
Answer/Explanation
Answer:
Explaination:
If [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 0 then points are collinear.
∴ \(\frac{-3}{2}\)(-2 – 4) + 6(4 – 3) + [(-3){3-(-2)}]
= \(\frac{-3}{2}\) × (-6) + 6 × 1 – 3 × 5
= 9 + 6 – 15 = 0.
∴ P, Q and R are collinear.
54. Find the area (in square units) of the triangle formed by the points A(a, 0), 0(0, 0) and B(0, b). [Foreign 2011]
Answer/Explanation
Answer:
Explaination:
A (a, 0), O(0, 0) and B(0, b)
ar(∆AOB) = \(\frac{1}{2}\)|a(0 – b) + 0{b – 0) + 0(0 -0)|
= \(\frac{1}{2}\)| -ab + 0 +0| = \(\frac{ab}{2}\)
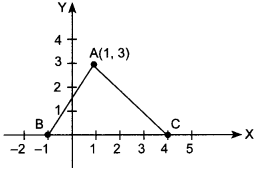
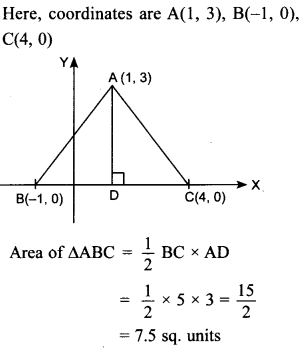
55. In figure, find the area of triangle ABC.
Answer/Explanation
Answer:
Explaination:
56. If area of the triangle given below is 20 square units, what are the coordinates of point C
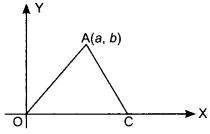
Answer/Explanation
Answer:
Explaination:
Drow AD ⊥ OC

∴ AD = b
and coordinates of C are (h, 0)
∴ OC = h
Area of ∆OAC = 20 sq. units
⇒ \(\frac{1}{2}\) × OC × AD = 20
h × b = 40
h = \(\frac{40}{b}\)
∴ Coordinates of C are (\(\frac{40}{b}\), 0)
We hope the given MCQ Questions for Class 10 Maths Coordinate Geometry with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 7 Coordinate Geometry Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.