Free PDF Download of CBSE Class 10 Maths Chapter 6 Triangles Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Triangles MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 6 Triangles
1. O is a point on side PQ of a APQR such that PO = QO = RO, then
(a) RS² = PR × QR
(b) PR² + QR² = PQ²
(c) QR² = QO² + RO²
(d) PO² + RO² = PR²
Answer
Answer: b
2. In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to
(a) 7.5 cm
(b) 3 cm
(c) 4.5 cm
(d) 6 cm
Answer
Answer: c
3. AABC is an equilateral A of side a. Its area will be…

Answer
Answer: a
4. In a square of side 10 cm, its diagonal = …
(a) 15 cm
(b) 10√2 cm
(c) 20 cm
(d) 12 cm
Answer
Answer: b
5. In a rectangle Length = 8 cm, Breadth = 6 cm. Then its diagonal = …
(a) 9 cm
(b) 14 cm
(c) 10 cm
(d) 12 cm
Answer
Answer: c
6. In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be…
(a) 16 × 12 cm²
(b) 96 cm²
(c) 8 × 6 cm²
(d) 144 cm²
Answer
Answer: b
7. In a rhombus if d1 = 16 cm, d2 = 12 cm, then the length of the side of the rhombus is
(a) 8 cm
(b) 9 cm
(c) 10 cm
(d) 12 cm
Answer
Answer: c
8. If in two As ABC and DEF, \(\frac{\mathrm{AB}}{\mathrm{DF}}=\frac{\mathrm{BC}}{\mathrm{FE}}=\frac{\mathrm{CA}}{\mathrm{ED}}\), then
(a) ∆ABC ~ ∆DEF
(b) ∆ABC ~ ∆EDF
(c) ∆ABC ~ ∆EFD
(d) ∆ABC ~ ∆DFE
Answer
Answer: d
9. It is given that ∆ABC ~ ∆DEF and \(\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{1}{5}\). Then \(\frac{\operatorname{ar}(D E F)}{\operatorname{ar}(A B C)}\) is equal to
(а) 5
(b) 25
(c) \(\frac{1}{25}\)
(d) \(\frac{1}{5}\)
Answer
Answer: b
10. In ∠BAC = 90° and AD ⊥ BC. A Then
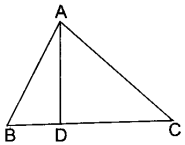
(а) BD.CD = BC²
(б) AB.AC = BC²
(c) BD.CD = AD²
(d) AB.AC = AD²
Answer
Answer: c
11. D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is
(a) 2.5
(b) 3
(c) 5
(d) 6
Answer
Answer: b
12. If ΔABC ~ ΔDEF and ΔABC is not similar to ΔDEF then which of the following is not true?
(a) BC.EF = AC.FD
(b) AB.ED = AC.DE
(c) BC.DE = AB.EE
(d) BC.DE = AB.FD
Answer
Answer: c
13. If in two triangles DEF and PQR, ZD = ZQ and ZR = ZE, then which of the following is not true?
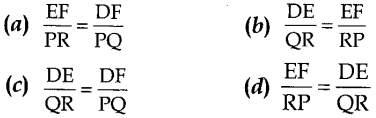
Answer
Answer: b
14. If ΔABC ~ ΔPQR, \(\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{1}{3}\) then \(\frac{\operatorname{ar}(PQR)}{\operatorname{ar}(BCA)}\) is
(a) 9
(b) 3
(c) 1/3
(d) 1/9
Answer
Answer: a
15. If ΔABC ~ ΔQRP, \(\frac{\operatorname{ar}(\mathrm{ABC})}{\operatorname{ar}(\mathrm{PQR})}=\frac{9}{4}\), AB = 18 cm and BC = 15 cm, then PR is equal to
(a) 10 cm
(b) 12 cm
(c) \(\frac{20}{3}\)cm
(d) 8 cm
Answer
Answer: a
16. If in triangles ABC and DEF,\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{FD}}\) , then they will be similar, if
(a) ∠B = ∠E
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠A = ∠F
Answer
Answer: c
17. In the given figure, \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) and ∠ADC = 70° ∠BAC =
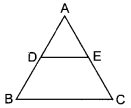
(a) 70°
(b) 50°
(c) 80°
(d) 60°
Answer/Explanation
Answer: d
Explaination:
∵ DE || BC
∴ ∠ABC = 70°.
(Corresponding angles) Using angle sum property of triangle ∠ABC + ∠BCA + ∠BAC = 180° ∠BCA = 60°.
18. In given figure, AD = 3 cm, AE = 5 cm, BD = 4 cm, CE = 4 cm, CF = 2 cm, BF = 2.5 cm, then
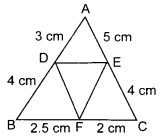
(a) DE || BC
(b) DF || AC
(c) EF || AB
(d) none of these
Answer/Explanation
Answer: c
Explaination:

19. If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true? [NCERT Exemplar Problems]
(a) BC . EF = AC . FD
(b) AB . EF = AC . DE
(c) BC . DE = AB . EF
(d) BC . DE = AB . FD
Answer/Explanation
Answer: c
Explaination:

20. If in two triangles ABC and PQR, \(\frac{\mathrm{AB}}{\mathrm{QR}}=\frac{\mathrm{BC}}{\mathrm{PR}}=\frac{\mathrm{CA}}{\mathrm{PQ}}\), then [NCERT Exemplar Problems]
(a) ΔPQR ~ ΔCAB
(b) ΔPQR ~ ΔABC
(c) ΔCBA ~ ΔPQR
(d) ΔBCA ~ ΔPQR
Answer/Explanation
Answer: a
Explaination:
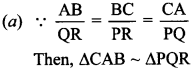
21. Match the column:

(a) 1 → A, 2 → B, 3 → C, 4→ D
(b) 1 → D, 2 → A, 3 → C, 4 → B
(c) 1 → B, 2 → A, 3 → C, 4 → D
(d) 1 → C, 2 → B, 3 → D, 4 → A.
Answer/Explanation
Answer: c
Explaination:
(c) Properties of triangles
22. In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are [NCERT Exemplar Problems]
(a) congruent but not similar
(b) similar but not congruent
(c) neither congruent nor similar
(d) congruent as well as similar
Answer/Explanation
Answer: b
Explaination: (b) Similar but not congruent
23. If in triangles ABC and DEF, \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{FD}}\) then they will be similar, when [NCERT Exemplar Problems]
(a) ∠B = ∠E
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠A = ∠F
Answer/Explanation
Answer: c
Explaination:
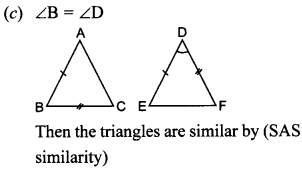
24. ABC and BDE are two equilateral triangles such that D is mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(a) 2 : 1
(b) 1:4
(c) 1:2
(d) 4:1
Answer/Explanation
Answer: d
Explaination:
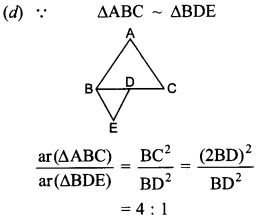
25. Sides of two similar triangles are in the ratio 3 : 7. Areas of these triangles are in the ratio
(a) 9 : 35
(b) 9 : 49
(c) 49 : 9
(d) 9 : 42
Answer/Explanation
Answer: b
Explaination:
(b) Ratio of areas of two similar triangles is the square of the ratio of their corresponding sides.
Required ratio = 9 : 49.
26. Sides of triangles are (i) 3 cm, 4 cm, 6 cm. (ii) 4 cm, 5 cm, 6 cm. (iii) 7 cm, 24 cm, 25 cm (iv) 5 cm, 12 cm, 14 cm. Which of these is right triangle?
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Answer/Explanation
Answer: c
Explaination:
On verification, triangle with sides 7 cm, 24 cm and 25 cm is a right triangle
∵ (25)² = (7)² + (24)².
27. If in two triangles DEF and PQR, ZD = ZQ and ZR = ZE, then which of the following is not true?

Answer/Explanation
Answer: b
Explaination: (b) Because ΔDEF ~ ΔQRP
28. “If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.” This theorem is known as _____ .
Answer/Explanation
Answer:
Explaination:
Thales Theorem or Basic Proportionality Theorem
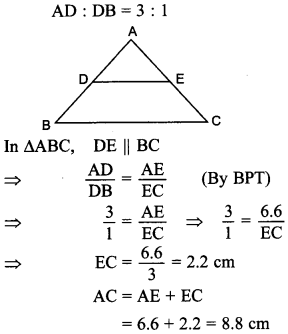
29. In ΔABC, D and E are points on sides AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 6.6 cm then find AC.
Answer/Explanation
Answer:
Explaination:
30. In the given figure, value of x (in cm) is _____ .
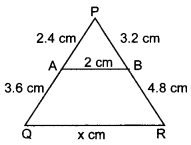
Answer/Explanation
Answer:
Explaination:

31. In the given figure, if ΔABC ~ ΔPQR
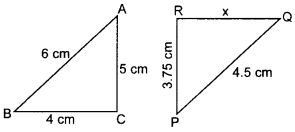
The value of x is_____ .
Answer/Explanation
Answer:
Explaination:
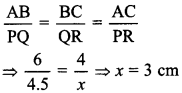
32. The perimeter of two similar triangles ABC and LMN are 60 cm and 48 cm respectively. If LM = 8 cm, then what is the length of AB?
Answer/Explanation
Answer:
Explaination:

33. In fig. ZM = ZN = 46°, express x in terms of a, b and c, where a, b and c are lengths of LM, MN and NK respectively.
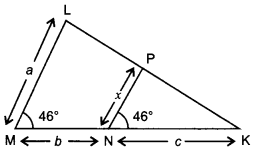
Answer/Explanation
Answer:
Explaination:

34. ΔABC ~ ΔPQR. Area of ΔABC = 81 cm² and area of ΔPQR =121 cm². If altitude AD = 9 cm, then PM = ______ .
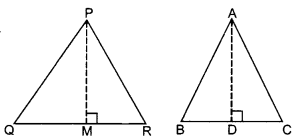
Answer/Explanation
Answer:
Explaination:
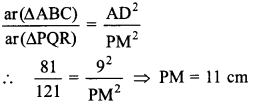
35. Given ΔABC ~ ΔPQR, if \(\frac{A B}{P Q}=\frac{1}{3}\), then find \(\frac{\operatorname{ar} \Delta \mathrm{ABC}}{\operatorname{ar} \Delta \mathrm{PQR}}\). [CBSE 2018]
Answer/Explanation
Answer:
Explaination:

36. In fig., DE || BC, AD = 1 cm and BD = 2 cm. What is the ratio of the ar(ΔABC) to the ar(ΔADE)? [Delhi 2019]

Answer/Explanation
Answer:
Explaination:
Given: In ΔABC, DE || BC
Also AD = 1 cm and BD = 2 cm
To find: ar(ΔABC) : ar(ΔADE)
As DE || BC (Given)
∠D = ∠B and ∠E = ∠C (Corresponding angles)
∴ ΔADE ~ ΔABC (By AA similarity)

ar(ΔABC) : ar(ΔADE) = 9:1.
37. In figure, S and T are points on the sides PQ and PR, respectively of APQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
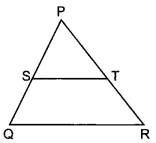
Answer/Explanation
Answer:
Explaination:
S and T are points on the sides PQ and PR of ΔPQR and PT = 2 cm, TR = 4 cm, ST || QR
In APST and ΔPQR,
∠S = ∠Q (Corresponding angles)
∠P = ∠P (Common)
∴ ΔPST ~ ΔPQR (AA similarity)

38. In ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm. The angle B is _____ .
Answer/Explanation
Answer:
Explaination:
AC² = 144 cm²
AB² = 108 cm²
BC² = 36 cm²
Now, AB² + BC²
= 144 = AC² B
∴ ∠B = 90°
39. The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is
(a) 9 cm
(b) 10 cm
(c) 8 cm
(d) 20 cm
Answer/Explanation
Answer: b
Explaination:
Diagonals of a Rhombus are perpendicular to each other and bisect each oSo AO = 8 cm
BO = 6 cm
∠AOB = 90°
In right angled ΔAOB
AB² = AO² + OB²
AB² = 8² + 6² = 64 + 36
AB =√100 = 10 cm.
40. The sides of a triangle are 30, 70 and 80 units. If an altitude is droped upon the side of length 80 units, the larger segment cut off on this side is______.
Answer/Explanation
Answer:
Explaination:
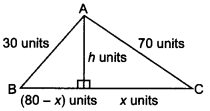
Now h² = 30² – (80 – x)²
Also h² = 70² – x²
⇒ 30² – (80 – x)² = 70² – x²
⇒ 160x = 10400
⇒ x=65 units.
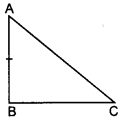
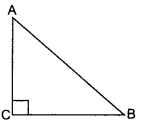
41. In Fig., ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
Answer/Explanation
Answer:
Explaination:
Given: AC = 4 cm
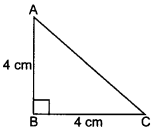
For isosceles triangle,
AC = BC
∴ BC = 4 cm
Using Pythagoras theorem,
AB² = AC2 + BC²
AB² = (4)2 + (4)²
⇒ AB² = 16 + 16 = 32
⇒ AB = A√32 = 4√2 cm.
We hope the given MCQ Questions for Class 10 Maths Triangles with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 6 Triangles Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.