Free PDF Download of CBSE Class 10 Maths Chapter 12 Areas Related to Circles Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Areas Related to Circles MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 12 Areas Related to Circles
Circle Multiple Choice Question 1. The area of the circle is 154 cm2. The radius of the circle is
(a) 7 cm
(b) 14 cm
(c) 3.5 cm
d) 17.5 cm
Answer/ Explanation
Areas Related To Circles Class 10 MCQ With Answer: dExplaination: Reason: Area of circle = 154 cm²
⇒ nr² = 154 cm2
⇒ \(\frac{22}{7}\) × r² = 154
⇒ r² = 154 × \(\frac{22}{7}\)
⇒ r² = 7 × 7 = 49
∴ r = √49 = 7
2. If angle of sector is 60°, radius is 3.5 cm then length of the arc is
(a) 3 cm
(b) 3.5 cm
(c) 3.66 cm
(d) 3.8 cm
Answer/ Explanation
Answer: c
Explaination: Reason: Here r = 3.5 cm = \(\frac{35}{10}\) = \(\frac{7}{2}\) cm θ = 60°
Length of arc = \(\frac{θ}{360}\) × 2πr = \(\frac{60}{360}\) × 2 × \(\frac{22}{7}\) = × \(\frac{7}{2}\) × \(\frac{1}{6}\) × 22 = \(\frac{11}{6\3}\) = 3.66 cm
Areas Related To Circles MCQs Question 3. The area of a quadrant of a circle whose circumference is 22 cm, is
![]()
Answer/ Explanation
Answer: d
Explaination: Reason: Here 2πr = 22 cm
2 × \(\frac{22}{7}\) × r = 22
⇒ r = 22 × \(\frac{7}{22}\) × \(\frac{1}{2}\) = \(\frac{7}{2}\) cm
∴ Area of quadrant of circle = \(\frac{1}{4}\)πr² = \(\frac{1}{4}\) × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) = \(\frac{77}{8}\) cm²
4. If 0 is the angle in degrees of a sector of a circle of radius V, then area of the sector is

Answer
Answer: b
5. A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze, is
(a) 77 cm²
(b) \(\frac{77}{2}\) cm²
(c) 154 cm²
(d) \(\frac{77}{4}\) cm²
Answer/ Explanation
MCQ on Areas Related To Circles With Answer: b
Explaination:

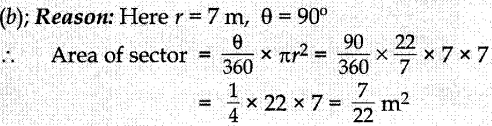
6. The area of the circle whose diameter is 21 cm is
(a) 346.5 cm²
(b) 37.68 cm²
(c) 18.84 cm²
(d) 19.84 cm²
Answer/ Explanation
Answer: a
Explaination: Reason: Here diameter = 21 cm
∴ Radius r = \(\frac{21}{2}\) cm
Area of the circle, A = πr²
∴ \(A=\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}=11 \times 3 \times \frac{21}{2}=\frac{693}{2}=346.5 \mathrm{cm}^{2}\)
7. The area of the sector of a circle with radius 6 cm and of angle 60° is
(a) 9.42 cm²
(b) 37.68 cm²
(c) 18.84 cm²
(d) 19.84 cm²
Answer/ Explanation
Answer: c
Explaination: Reason: Here r = 6 cm, θ = 60°
Area of the sector = \(\frac{θ}{360}\)
∴ Area = \(\frac{60}{360}\) × 3.14 × 6 × 6 = \(\frac{1}{6}\) × 3.14 × 6 × 6 = 3.14 × 6 = 18.84 cm²
8. The area of a circle whose circumference is 22 cm, is
(a) 11 cm²
(b) 38.5 cm²
(c) 22 cm²
(d) 77 cm²
Answer/ Explanation
Answer: b
Explaination:

9. The area of a circle is 154 cm2. Its diameter is
(a) 7 cm
(b) 14 cm
(c) 21 cm
(d) 28 cm
Answer/ Explanation
Answer: b
Explaination: Reason: Here area of the circle, A = 154 cm², Radius, r = ?
Area of the circle = 154 cm² …(Given)
∴ πr² = 154
⇒ \(\frac{22}{7}\) × r² = 154
⇒ r² = 154 × latex]\frac{7}{22}[/latex] = 7 × 7
⇒ r = 7 cm
∴ Diameter of the circle = 2 × r = 2 × 7 = 14 cm
10. The length of the minute hand of a clock is 14 cm. The area swept by the minute hand in 5 minutes is
(a) 153.9 cm²
(b) 102.6 cm²
(c) 51.3 cm²
(d) 205.2 cm²
Answer/ Explanation
Answer: c
Explaination: Reason: Angle swept by the minute hand in 1 minute = (360° ÷ 60) = 6°
∴ θ = 30°
∴ Angle swept by the minute hand in 5 minutes = 6° × 5 = 30°
Length of minute hand (r) = 14 cm
∴ Area swept = \(\frac{θ}{360}\)πr² = \(\frac{30}{360}\) × \(\frac{22}{7}\) × 14 × 14 = \(\frac{154}{3}\) = 51.3 cm²
MCQ Questions For Class 10 Maths Areas Related To Circles Question 11. The radii of two circles are 19 cm and 9 cm respectively. The radius of the circle which has circumference equal to the sum of the circumference of two circles is
(a) 35 cm
(b) 10 cm
(c) 21 cm
(d) 28 cm
Answer/ Explanation
Answer: d
Explaination: Reason: Let the radii of two circles be r1 and r2 and the radius of large circle be r.
∴ r1 = 19 cm, r2 = 9 cm
Circumference of two circles = C1+ C2 …(where C = circle)
= 2πr1 + 2πr2 = 2π × 19 + 2π × 9 = 38π + 18π = 56π
∴ Circumference of large circle = 56π
⇒ 2πr = 56π
⇒ r = 28
∴ Radius of large circle = 28 cm
12. The area of the circle that can be inscribed in a square of side 6 cm, is
(a) 18π cm²
(b) 12π cm²
(c) 9π cm²
(d) 14π cm²
Answer/ Explanation
Answer: c
Explaination: Reason: Size of square = 6 cm, radius = \(\frac{6}{2}\) = 3 cm;
Area of the circle = πr² = π × 3 × 3 = 9π cm²
13. The radii of two circles are 4 cm and 3 cm respectively. The diameter of the circle having area equal to the sum of the areas of the two circles (in cm) is [Delhi 2011]
(a) 5
(b) 7
(c) 10
(d) 14
Answer/ Explanation
Answer: c
Explaination:

MCQ on Area Related To Circles Class 10 Question 14. The perimeter (in cm) of a square circumscribing a circle of radius a cm, is [AI2011]
(a) 8 a
(b) 4 a
(c) 2 a
(d) 16 a
Answer/ Explanation
Answer: a
Explaination:
(a) Side of a square circumscribing a circle of radius a cm = diameter of circle = 2 a cm
∴ Perimeter of the square
= 4 × 2a = 8a cm
15. If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is
(a) 4 units
(b) n units
(c) 8 units
(d) 2 units
Answer/ Explanation
Answer: c
Explaination:
(c) πr² = 2πr × 2
⇒ r = 4
⇒ 2r = 8 units
16. If the circumference of a circle is 352 metres, then its area in square metres is
(a) 5986
(b) 6589
(c) 7952
(d) 9856
Answer/ Explanation
Answer: d
Explaination:

Area Related To Circle Class 10 MCQ Question 17. The diameter of a wheel is 1.26 m. The distance travelled in 500 revolutions is
(a) 2670 m
(b) 2880 m
(c) 1980 m
(d) 1596 m
Answer/ Explanation
Answer: c
Explaination:
(c) Radius of the wheel = \(\frac{1.26}{2}\) = 0.63 m
Distance travelled in one revolution
= 2πr = 2 × \(\frac{22}{7}\) × 0.63
= 3.96 m
∴ Distance travelled in 500 revolutions
= 500 × 3.96
= 1980 m.
18. If the sum of the circumferences of two circles with radii Rj and R2 is equal to the circumference of a circle of radius R, then [NCERT Exemplar Problems]
(a) R1 + R2 = R
(b) R1 + R2 > R
(C) R1 + R2 < R
(d) nothing definite can be said about the relation among Rp1, R2 and R.
Answer/ Explanation
Answer: a
Explaination:
(a) 2πR1 + 2πR2 = 2πR
⇒ R1 + R2 = R.
19. If the circumference of a circle and the perimeter of a square are equal, then [NCERT Exemplar Problems]
(a) area of the circle = area of the square
(b) area of the circle > area of the square
(c) area of the circle < area of the square
(d) nothing definite can be said about the relation between the areas of the circle and square.
Answer/ Explanation
Answer: b
Explaination:
(b) Let circumference of a circle = C
2πr = C C
⇒ r = \(\frac{C}{2π}\)
Perimeter of a square = C
⇒ 4a = C
⇒ a = \(\frac{C}{4}\)
MCQ on Area Related To Circles Question 20. Area of the largest triangle that can be inscribed in a semi-circle of radius r units is [NCERT Exemplar Problems]
(a) r² sq. units
(b) \(\frac{1}{2}\) r² sq. units
(c) 2 r² sq. units
(d) √2 r² sq. units
Answer/ Explanation
Answer: a
Explaination:

21. Match the columns

(a) 1 → A, 2 → C, 3 → D, 4 → E
(b) 1 → B, 2 → C, 3 → F, 4 → E
(c) 1 → D, 2 → B, 3 → A, 4 → F
(d) 1 → D, 2 → B, 3 → E, 4 → F
Answer/ Explanation
Answer: c
Explaination: (c) Formulae
22. In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. The area of the shaded region (in cm2) is [Using π = \(\frac{22}{7}\)] [Foreign 2012]

(a) 77
(b) 154
(c) 44
(d) 22
Answer/ Explanation
Answer: a
Explaination:
(a) Area of shaded region = area of sector with angle
(60° + 80° + 40°) = \(\frac{180^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 7 \times 7\)
= 77 cm²
Areas Related To Circles Question 23. If the difference between the and the radius of of a circle is 37 cm, then 22 using π = \(\frac{22}{7}\) the circumference (in cm) of the circle is: [Delhi 2013]
(a) 154
(b) 44
(c) 14
(d) 7
Answer/ Explanation
Answer: b
Explaination:

24. If 7i is taken as \(\frac{22}{7}\), the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is [AI2013]
(a) 2.2
(b) 1.1
(c) 9.625
(d) 96.25
Answer/ Explanation
Answer: b
Explaination:
(b) Distance covered by a wheel in one
revolution = 2 πr = 2 × \(\frac{22}{7}\) × \(\frac{35}{2}\)
= 110 cm = 1.1 m
Circle MCQ Pdf Question 25. If the circumferences of two circles are in the ratio 4 : 9, then the ratio in their area is
(a) 9 : 4
(b) 4 : 9
(c) 2 : 3
(d) 16 : 81
Answer/ Explanation
Answer: d
Explaination:

26. The ratio of the areas of the incircle and circumcircle of a square is
(a) 1 : 2
(b) 1 : 3
(c) 1 : 4
(d) 1 : √2
Answer/ Explanation
Answer: a
Explaination:
(a) Let side of square = x units
∴ Diagonal of the square = √2 x units
Diameter of the incircle = x units
Diameter of the circumcircle = √2 x units

27. A circular wire of radius 42 cm is cut and bent into the form of a rectangle whose sides are in the ratio of 6 : 5. The smaller side of the rectangle is
(a) 30 cm
(b) 60 cm
(c) 70 cm
(d) 80 cm
Answer/ Explanation
Answer: b
Explaination:
(b) Length of wire = 2πrr = 2πr × 42
= 2 × \(\frac{22}{7}\) × 42 = 264 cm
Let sides of rectangle are 6x and 5x
⇒ 2(6x + 5x) = 264
⇒ 11x = 132
⇒ x = 12
∴ Smaller side = 12 × 5 = 60 cm
28. Match the columns.

(a) 1 → B, 2 → C, 3 → D, E → 4
(b) 1 → B, 2 → D, 3 → C, E → 4
(c) 1 → A, 2 → C, 3 → D, E → 4
(d) 1 → B, 2 → C, 3 → D, E → 4
Answer/ Explanation
Answer: b
Explaination: (b) Formulae
29. ABC is an equilateral triangle. The area of the shaded region if the radius of each of the circle is 1 cm, is


Answer/ Explanation
Answer: c
Explaination:

30. ABCDEF is any hexagon with different vertices A, B, C, D, E and F as the centres of circles with same radius r are drawn. The area of the shaded portion is
(a) πr²
(b) 2πr²
(c) 3πr²
(d) 4πr²
Answer/ Explanation
Answer: b
Explaination:

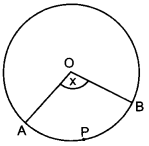
31. In the figure, PQRS is a square and O is centre of the circle. If RS = 10 √2, then area of shaded region is

(a) 90 π – 90
(b) 80 π – 80
(c) 50 π-100
(d) 100 π – 100
Answer/ Explanation
Answer: c
Explaination:
(c) Diagonal of square = √2 × (10√2) = 20 units
∴ Diameter of circle = 20 units
Area of circle = π × (10)² = 100π sq.units
Area of square = (10√2)² = 200 sq. units
Area of circle not included in the square = (100π – 200) sq.units
∴ Area of shaded portion = \(\frac{1}{2}\)(100π – 200)
= 50π – 100.
32. The diameter of the wheel of a bus is 1.4 m. The wheel makes 10 revolutions in 5 seconds. The speed of the vehicle (in kmph) is ______ .
Answer/ Explanation
Answer:
Explaination:

33. The area of a quadrant of a circle whose circumference is 44 cm is ______ .
Answer/ Explanation
Answer:
Explaination:

34. If the wheel of an engine of a train is 4\(\frac{2}{7}\)m in circumference makes seven revolutions in 4 seconds, then the speed of the train is _____ km/h.
Answer/ Explanation
Answer:
Explaination:

35. The area of the largest possible square inscribed in a circle of unit radius (in sq. units) is ______.
Answer/ Explanation
Answer:
Explaination:
2 units
Hints: Diameter of circle = 2 units
∴ Diagonal of the square = 2 units
Side of the square = \(\frac{2}{\sqrt{2}}\) = √2 units
∴ Area of the square = (√2)² = 2 sq. units
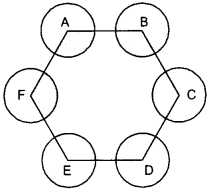
36. In the fig., O is the centre of a circle. The area of sector OAPB is \(\frac{5}{18}\) of the area of the circle. Find x.
Answer/ Explanation
Answer:
Explaination:

37. Find the perimeter of the given figure, where \(\widehat{\mathrm{AED}}\) is a semicircle and ABCD is a rectangle.
Answer/ Explanation
Answer:
Explaination:

Length of \(\widehat{\mathrm{AED}}\) = πr
= π x 7 cm = 7π cm
AB + BC + DC = 20 + 14 + 20 = 54 cm
∴ Perimeter of figure = (7π + 54) cm
38. A bicycle wheel makes 5000 revolutions in moving 11 km. Find the diameter of the wheel. (use π = \(\frac{22}{7}\))
Answer/ Explanation
Answer:
Explaination:

39. A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of pendulum, (use π = \(\frac{22}{7}\))
Answer/ Explanation
Answer:
Explaination:

40. An arc of a circle is of length 5TI cm and the sector it bounds has an area of 20π cm². Find the radius of the circle.
Answer/ Explanation
Answer:
Explaination:


41. If the diameter of a semicircular protractor is 14 cm, then find its perimeter. [π = \(\frac{22}{7}\)]
Answer/ Explanation
Answer:
Explaination:

42. Find the perimeter of the shaded region in figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles. [Use π = \(\frac{22}{7}\)]
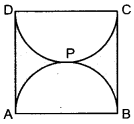
Answer/ Explanation
Answer:
Explaination:
Perimeter = AD + BC + length of DPC + length of APB
= 14 + 14 + πr + πr
= 28 + 2 × \(\frac{22}{7}\) × \(\frac{14}{2}\)= 72 cm
We hope the given MCQ Questions for Class 10 Maths Areas Related to Circles with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 12 Areas Related to Circles Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.