Free PDF Download of CBSE Maths Multiple Choice Questions for Class 12 with Answers Chapter 7 Integrals. Maths MCQs for Class 12 Chapter Wise with Answers PDF Download was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Integrals MCQs Pdf with Answers to know their preparation level.
Integrals Class 12 Maths MCQs Pdf
1. Given ∫ 2x dx = f(x) + C, then f(x) is

Answer/Explanation
Answer: c
Explaination:

2.
![]()
(a) sin² x – cos² x + C
(b) -1
(c) tan x + cot x + C
(d) tan x – cot x + C
Answer/Explanation
Answer: d
Explaination:


3.
![]()
(a) 2(sin x + x cos θ) + C
(b) 2(sin x – x cos θ) + C
(c) 2(sin x + 2x cos θ) + C
(d) 2(sin x – 2x cos θ) + C
Answer/Explanation
Answer: a
Explaination:

4. ∫cot²x dx equals to
(a) cot x – x + C
(b) cot x + x + C
(c) -cot x + x + C
(d) -cot x – x + C
Answer/Explanation
Answer: d
Explaination: (d), ∫ (cosec²x -1)dx = -cot x – x + C
5.
![]()
(a) log |sin x + cos x|
(b) x
(c) log |x|
(d) -x
Answer/Explanation
Answer: d
Explaination:

6. If ∫ sec²(7 – 4x)dx = a tan (7 – 4x) + C, then value of a is
(a) 7
(b) -4
(c) 3
(d) \(-\frac{1}{4}\)
Answer/Explanation
Answer: d
Explaination:
(d), ∫sec²(7 – 4x)dx = \(\frac{\tan (7-4 x)}{-4}\) + C = –\(\frac{1}{4}\) tan (7 – 4x) + C.
7. The value of X for which
![]()
(a) 1
(b) loge4
(c) loe4 e
(d) 4
Answer/Explanation
Answer: b
Explaination:

8.

Answer/Explanation
Answer: c
Explaination:

9.
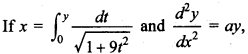
then value of a is equal to
(a) 3
(b) 6
(c) 9
(d) 1
Answer/Explanation
Answer: c
Explaination:

10.
![]()

Answer/Explanation
Answer:
Explaination:
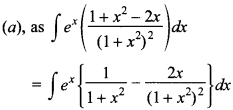
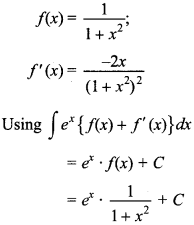
11.
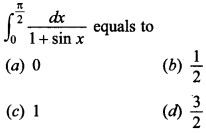
Answer/Explanation
Answer: c
Explaination:
12.
![]()
(a) I1 > I2
(b) I2 > I1
(c) I1 = I2
(d) I1 > 2I2
Answer/Explanation
Answer: b
Explaination:

13. If a is such that \(\int_{0}^{a} x d x\) ≤ a + 4, then
(a) 0 ≤ a ≤ 4
(b) -2 ≤ a ≤ 0
(c) a ≤ -2 or a ≤ 4
(d) -2 ≤ a ≤ 4
Answer/Explanation
Answer: d
Explaination:
(d), as \(\int_{0}^{a}\) x dx ≤ a + 4
⇒ \(\frac{a²}{2}\) ≤ a + 4
⇒ a² – 2a — 8 ≤ 0
⇒ (a – 1)² ≤ (3)²
⇒ -3 ≤ a – 1 ≤ 3
⇒ -2 ≤ a ≤ 4
14. If \(\frac{d}{dx}\) f(x) = g(x), then antiderivative of g(x) is ________ .
Answer/Explanation
Answer:
Explaination:
f(x), as \(\frac{d}{dx}\) f(x) = g(x)
⇒ ∫ g(x)dx = f(x).
15. Derivative of a function is unique but a function can have infinite antiderivatives. State true or false.
Answer/Explanation
Answer:
Explaination: True, as ∫ f(x)dx = g(x) + C, C is constant can take different values but \(\frac{d}{dx}\) [g(x) + C]
=f(x) only
16.
![]()
Answer/Explanation
Answer:
Explaination: \(\frac{2}{3}\) ∫ cosec x . cot x dx = –\(\frac{2}{3}\) ∫ cosec x + C
17. Find ∫(ax + b)3dx [AI 2011]
Answer/Explanation
Answer:
Explaination:
![]()
18. If ∫(ax + b)² dx = f(x) + C, find f(x)
Answer/Explanation
Answer:
Explaination:
![]()
19. We have \(\frac{d}{dx}\)(3x² + sin x – ex) = 6x + cos x -ex. Represent the expression in the form of anti derivative.
Answer/Explanation
Answer:
Explaination:
\(\frac{d}{dx}\) (3x² + sin x – ex) = 6x + cos x – ex
⇒ ∫ (6x + cos x – ex) = 3x² + sin x – ex
20.
![]()
Answer/Explanation
Answer:
Explaination:
![]()
21.
![]()
Answer/Explanation
Answer:
Explaination:

22. Evaluate ∫ (sin x + cos x)² dx
Answer/Explanation
Answer:
Explaination:
∫ (sin x + cos x)² dx = ∫ (sin²x + cos²x + 2sin x cos x)dx
= ∫(1 + sin 2x)dx = x – \(\frac{\cos 2 x}{2}\) + C
23.

Answer/Explanation
Answer:
Explaination:

24.
![]()
Answer/Explanation
Answer:
Explaination:
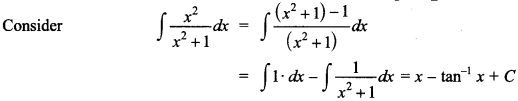
25. Find ∫(ex log a + ea log x + ea log a)dx
Answer/Explanation
Answer:
Explaination:
![]()
26. Evaluate \(\int e^{\frac{1}{2} \log x} d x\).
Answer/Explanation
Answer:
Explaination:

27.
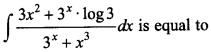
(a) 3x + x3 + C
(b) log |3x + x3| + C
(c) 3x²+ 3x loge 3 +C
(d) log |3x² + 3x loge 3| + C
Answer/Explanation
Answer: d
Explaination:
![]()
28.
![]()
Answer/Explanation
Answer:
Explaination:

29.
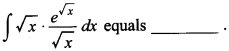
Answer/Explanation
Answer:
Explaination:
![]()
30.
![]()
Answer/Explanation
Answer:
Explaination:

31. Find ∫ sec² (7 – x)dx
Answer/Explanation
Answer:
Explaination:

32. Find \(\int \frac{\sin \sqrt{x}}{\sqrt{x}} d x\)
Answer/Explanation
Answer:
Explaination:

33. Find ∫2x sin(x² + 1) dx
Answer/Explanation
Answer:
Explaination:

34.

Answer/Explanation
Answer:
Explaination:

35.
![]()
Answer/Explanation
Answer:
Explaination:

36.
![]()
Answer/Explanation
Answer:
Explaination:

37.
![]()
Answer/Explanation
Answer:
Explaination:

38.
![]()
Answer/Explanation
Answer:
Explaination:

39.
![]()
Answer/Explanation
Answer:
Explaination:
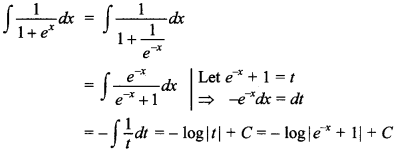
40.
![]()
Answer/Explanation
Answer:
Explaination:

41.
![]()
Answer/Explanation
Answer:
Explaination:

42.
![]()
Answer/Explanation
Answer:
Explaination:

43.
![]()
Answer/Explanation
Answer:
Explaination:
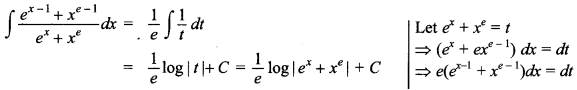
44. Evaluate ∫ sec4 x tan x dx
Answer/Explanation
Answer:
Explaination:
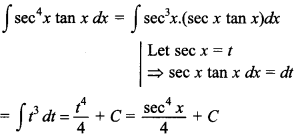
45.
![]()
Answer/Explanation
Answer:
Explaination:

46.
![]()
Answer/Explanation
Answer:
Explaination:
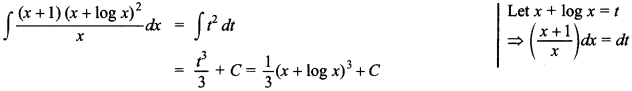
47. Find ∫ cot x . log(sin x) dx [NCERT]
Answer/Explanation
Answer:
Explaination:
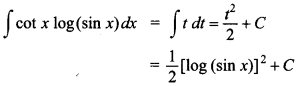

48.
![]()
Answer/Explanation
Answer:
Explaination:

49. Find ∫(ex + 3x)² (ex + 3)dx
Answer/Explanation
Answer:
Explaination:
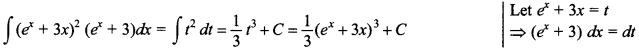
50.
![]()
Answer/Explanation
Answer:
Explaination:
![]()
51.
![]()
Answer/Explanation
Answer:
Explaination:
![]()
52. Find ∫ (cosx – sinx)² dx
Answer/Explanation
Answer:
Explaination:

53. Evaluate \(\int \sqrt{1+\sin \frac{x}{4}} d x\)
Answer/Explanation
Answer:
Explaination:

54.
![]()
Answer/Explanation
Answer:
Explaination:
![]()
55.
![]()
Answer/Explanation
Answer:
Explaination:
![]()
56.
![]()
Answer/Explanation
Answer:
Explaination:

57.
![]()
Answer/Explanation
Answer:
Explaination:

58.
![]()
Answer/Explanation
Answer:
Explaination:
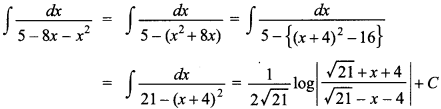
59.
![]()
Answer/Explanation
Answer:
Explaination:

60. ∫ ex sec x(1 + tan x)dx = ________ + C.
Answer/Explanation
Answer:
Explaination:
ex sec x, as ∫ex (sec x + sec x tan x) dx,
i.e. f(x) = sec x
f'(x) = sec x tan x,
using formula ∫ ex {f(x) + f'(x)}dx
= ex f(x) + C
61. If \(\int_{-1}^{4}\) f(x) dx =4 and \(\int_{2}^{4}\) (3 – f(x))dx = 7, then the value of \(\int_{-2}^{-1}\) f(x) dx is ________ .
Answer/Explanation
Answer:
Explaination:


62.
![]()
Answer/Explanation
Answer:
Explaination:

63.
![]()
Answer/Explanation
Answer:
Explaination:
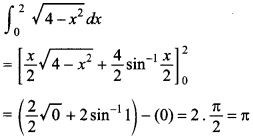
64.

Answer/Explanation
Answer:
Explaination:

65.
![]()
Answer/Explanation
Answer:
Explaination:
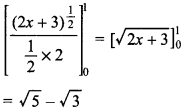
66. If \(\int_{0}^{a}\) 3x² dx = 8 write the value of a. [Foreign 2017]
Answer/Explanation
Answer:
Explaination:

67. Evaluate. \(\int_{2}^{3}\) 3x dx [Delhi 2017]
Answer/Explanation
Answer:
Explaination:

68.
![]()
Answer/Explanation
Answer:
Explaination:

69. \(\int_{0}^{2a}\)f(x)dx = 2 \(\int_{0}^{a}\) f(x)dx if f(2a -x)= f(x). State true or false.
Answer/Explanation
Answer:
Explaination: True; result
70.
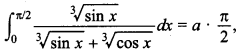
then value of a is ________ .
Answer/Explanation
Answer:
Explaination:

71.
![]()
Answer/Explanation
Answer:
Explaination:

72. \(\int_{-1}^{1}\) |(1 – x)| dx is equal to ________ .
Answer/Explanation
Answer:
Explaination:
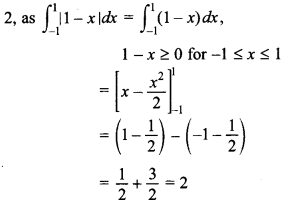
73.

is equal to 0.State true or false.
Answer/Explanation
Answer:
Explaination:
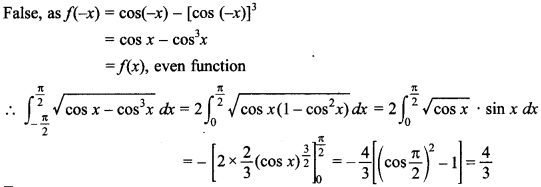
74. The value of \(\int_{0}^{\pi}\) | cos x|dx is 2. State true or false.
Answer/Explanation
Answer:
Explaination:

75. The value of \(\int_{-\pi}^{\pi}\) sin3x cos²x dx is ________ .
Answer/Explanation
Answer:
Explaination: 0, as f(x) = sin3 x. cos² x dx is an odd function
76.
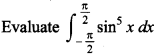
Answer/Explanation
Answer:
Explaination:
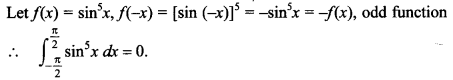
77.
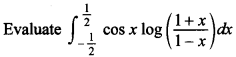
Answer/Explanation
Answer:
Explaination:

78.
![]()
Answer/Explanation
Answer:
Explaination:
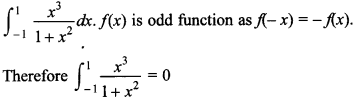
79.
![]()
Answer/Explanation
Answer:
Explaination:

80. Evaluate \(\int_{-1}^{1}\) x|x|dx
Answer/Explanation
Answer:
Explaination:
Consider \(\int_{-1}^{1}\) x|x| dx
f(x) = x|x|, f(-x) = (-x)|-x| = -x|x| = -f(x)
Odd function.
∴ \(\int_{-1}^{1}\) x|x|dx = 0
[using \(\int_{-a}^{a}\) f(x) = 0, if f(x) is odd function]
81. Evaluate \(\int_{0}^{2\pi}\) cos5x dx [Foreign 2017]
Answer/Explanation
Answer:
Explaination:

82.
![]()
Answer/Explanation
Answer:
Explaination:

83. Evaluate \(\int_{0}^{1}\) [2x]dx
Answer/Explanation
Answer:
Explaination:
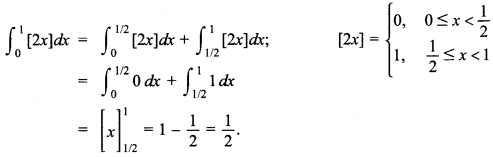
84. Evaluate \(\int_{1}^{4}\) f(x) dx, where

Answer/Explanation
Answer:
Explaination:

85.
![]()
Answer/Explanation
Answer:
Explaination:
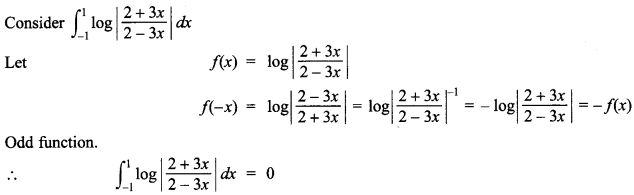
86. Evaluate \(\int_{-\pi}^{\pi}\) (sin-93 x + x295) dx
Answer/Explanation
Answer:
Explaination:
\(\int_{-\pi}^{\pi}\) (sin-93 x + x295)dx,f(x) is odd function as f(-x) = -f(x)
∴ \(\int_{-\pi}^{\pi}\) (sin-93 x + x295) dx=0
87.

Answer/Explanation
Answer:
Explaination:

88.

Answer/Explanation
Answer:
Explaination:

89.
![]()
Answer/Explanation
Answer:
Explaination:

90. \(\int_{1}^{e}\) log x. dx
Answer/Explanation
Answer:
Explaination:
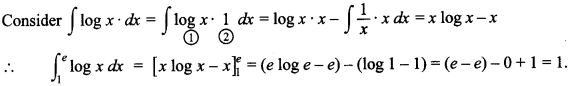
91. Evaluate \(\int_{0}^{1}\) x(1 – x)89dx
Answer/Explanation
Answer:
Explaination:
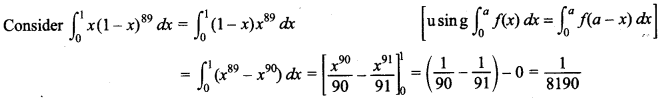
92.
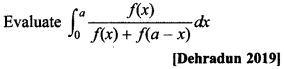
Answer/Explanation
Answer:
Explaination:

93. Evaluate \(\int_{0}^{1}\) x²(1 -x)ndx
Answer/Explanation
Answer:
Explaination:
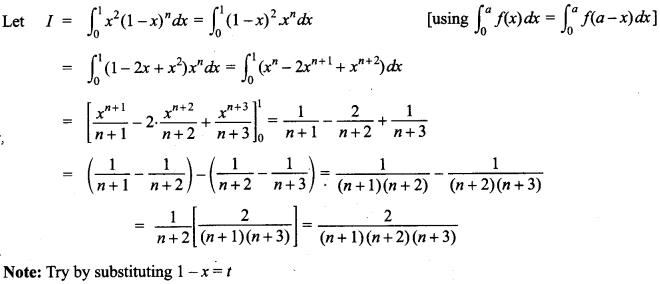
94.
![]()
Answer/Explanation
Answer:
Explaination:
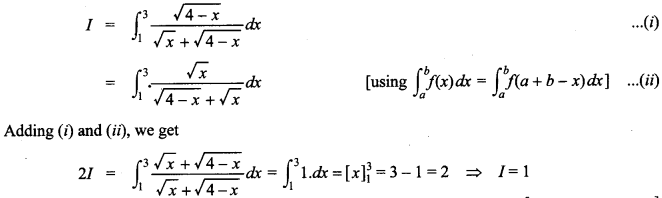
95. Evaluate \(\int_{0}^{\pi}\) |cos x|dx [DoE]
Answer/Explanation
Answer:
Explaination:

We hope the given Maths MCQs for Class 12 with Answers Chapter 7 Integrals will help you. If you have any query regarding CBSE Class 12 Maths Integrals MCQs Pdf, drop a comment below and we will get back to you at the earliest.