Free PDF Download of CBSE Maths Multiple Choice Questions for Class 12 with Answers Chapter 5 Continuity and Differentiability. Maths MCQs for Class 12 Chapter Wise with Answers PDF Download was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Continuity and Differentiability MCQs Pdf with Answers to know their preparation level.
Continuity and Differentiability Class 12 Maths MCQs Pdf
1. Given functions f(x) = \(\frac{x^{2}-4}{x-2}\) and g(x) = x + 2, x <= R. Then which of the following is correct?
(a) f is continuous at x = 2,
g is continuous at x = 2
(b) f is continuous at x = 2,
g is not continuous at x = 2
(c) f is not continuous at x = 2,
g is continuous at x = 2
(d) f is not continuous at x = 2,
g is not continuous at x = 2
Answer/Explanation
Answer: c
Explaination: (c), as f(2) is not defined so / is not continuous at x = 2 ‘g’ is a polynomial function, so continuous at x = 2.
2.

Answer/Explanation
Answer: d
Explaination:

3.
![]()
for x = 2, then value of k for which f is continuous is
(a) -2
(b) -1
(c) 0
(d) 1
Answer/Explanation
Answer: d
Explaination:
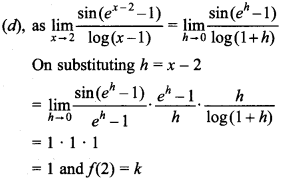
4. A function /is said to be continuous for x ∈ R, if
(a) it is continuous at x = 0
(b) differentiable at x = 0
(c) continuous at two points
(d) differentiable for x ∈ R
Answer/Explanation
Answer: d
Explaination: (d), as differentiable functions is continuous also.
5. Afunction

is continuous at x = 0 for
(a) k = 1
(b) k = 2
(c) k = \(\frac{1}{2}\)
(d) k = \(\frac{3}{2}\)
Answer/Explanation
Answer: a
Explaination:

6. Write the number of points where f(x) = |x + 2| + |x – 3| is not differentiable.
(a) 2
(b) 3
(c) 0
(d) 1
Answer/Explanation
Answer: a
Explaination: (a), as f(x) = |x – a| is continuous at x = a but not differentiable thereat.
7. Derivative of cot x° with respect to x is
(a) cosec x°
(b) cosec x° cot x°
(c) -1° cosec2 x°
(d) -1° cosec x° cot x°
Answer/Explanation
Answer: c
Explaination:

8.

![]()
Answer/Explanation
Answer: a
Explaination:

9. If f(x) = \(\log _{x^{2}}(\log x)\), then f(e) is
(a) 0
(b) 1
(c) \(\frac{1}{e}\)
(d) \(\frac{1}{2e}\)
Answer/Explanation
Answer: d
Explaination:

10. If f(x) = ex and g(x) = loge x, then (gof)’ (x) is
(a) 0
(b) 1
(c) e
(d) 1 + e
Answer/Explanation
Answer: b
Explaination:

11.
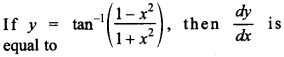

Answer/Explanation
Answer:
Explaination:
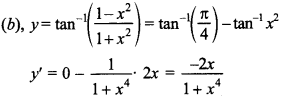
12. If y = xx-∞, , then x(l -y log x)\(\frac{d y}{d x}\) is equal to
(a) x²
(b) y²
(c) xy²
(d) x²y
Answer/Explanation
Answer: b
Explaination:

13. The derivative of sin x with respect to log x is
(a) cos x
(b) x cos x
(c) \(\frac{\cos x}{\log x}\)
(d) \(\frac{1}{x}\) cos x
Answer/Explanation
Answer: b
Explaination:
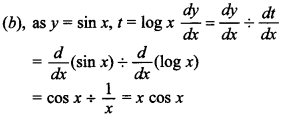
14. Ify = Ae5x,+ Be-5x x then \(\frac{d^{2} y}{d x^{2}}\) is equal to
(a) 25y
(b) 5y
(c) -25y
(d) 10y
Answer/Explanation
Answer:
Explaination:

15. Given the function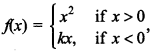
the function is continuous at x = 0, state true or false.
Answer/Explanation
Answer:
Explaination: False, as ‘f’ is not defined at x = 0. i.e.f (0) does not exist.
46. The function f(x) = \(\frac{x+1}{1+\sqrt{1+x}}\) continuous at x = 0 if/(0) is _________ .
Answer/Explanation
Answer:
Explaination:
![]()
17. A function f(x) = \(\frac{x}{x-5}\) x ∈ R, is a continuous function. State true or false.
Answer/Explanation
Answer:
Explaination: False, as for x = 5, f(5) is not defined.
18. A function f(x) = sin x + cos x is continuous function. State true or false.
Answer/Explanation
Answer:
Explaination: True, as sum of two continuous functions is a continuous function.
19. Discuss the continuity of the function fix)= \(\frac{1}{x-5}\) for x ∈ R.
Answer/Explanation
Answer:
Explaination: f(x) = \(\frac{1}{x-5}\), as f(5) is not defined, therefore function is not continuous at x = 5.
20. Discuss the continuity of the function
![]()
Answer/Explanation
Answer:
Explaination:
f(x)= \(\frac{x^{2}-25}{x-5}\), x ≠ 5. As x ≠ 5, therefore, value of function exists for all x(≠5) ∈ R.
Also \(\lim _{x \rightarrow a}\) f(x) = f(a) = a + 5, (a ≠ 5). Hence, continuous.
21. Check whether the function f(x) = 2x² + 1 is continuous at x = 0.
Answer/Explanation
Answer:
Explaination: f(x) = 2x² + 1, as \(\frac{x^{2}-25}{x-5}\) f(x) = f(0) = 1. Hence, continuous
22. Give an example of a function which is continuous but not differentiable at exactly two points.
Answer/Explanation
Answer:
Explaination:
We know function f(x)=|x – a| is continuous at x = a but not differentiable at x = a.
∴ functions |x| and |x – 1| are continuous but not differentiable at x = 0 and 1.
∴ function is h(x) = |x| + |x – 1|.
23. Determine the value of the constant ‘k’

Answer/Explanation
Answer:
Explaination:

24. Determine the value of ‘k’ for which the following function is continuous at x = 3:

Answer/Explanation
Answer:
Explaination:

25. For what value of ‘k’ is the function

continuous at x = 0?
Answer/Explanation
Answer:
Explaination:
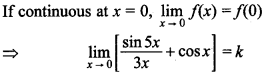

26. Find the value of k, so that the function
![]()
is continuous at x = 1
Answer/Explanation
Answer:
Explaination:

27. Determine the value of the constant ‘k’ so that the function

is continuous at x = 0. [Delhi]
Answer/Explanation
Answer:
Explaination:

28. For what value of ‘k’ is the function

continuous at x = 0? [Foreign]
Answer/Explanation
Answer:
Explaination:

29. The derivative of
![]()
State true or false.
Answer/Explanation
Answer:
Explaination:

30. Find \(\frac{d y}{d x}\), if x² + y² = 5
Answer/Explanation
Answer:
Explaination:
31. Differentiate sin-1x², with resepct to x.
Answer/Explanation
Answer:
Explaination:

32. Find \(\frac{d y}{d x}\), if sin y + x = log x
Answer/Explanation
Answer:
Explaination:

33. Find \(\frac{d y}{d x}\) at x = 1, y = \(\frac{\pi}{4}\) if sin²y + cos xy = K. [Delhi 2017]
Answer/Explanation
Answer:
Explaination:
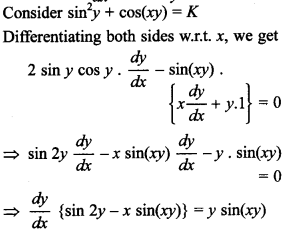

34. Differentiate tan-1 \(\left(\frac{1+\cos x}{\sin x}\right)\) with respect to x. [CBSE 2018]
Answer/Explanation
Answer:
Explaination:

35. If y = 2√x, then \(\frac{d y}{d x}\) is _______ .
Answer/Explanation
Answer:
Explaination:

36. If y = log (tan x) + log (cot x), then \(\frac{d y}{d x}\) is _______ .
Answer/Explanation
Answer:
Explaination:

37. If \(f(x)=9^{x^{2}+2 x}\), then f(-1) is _______ .
Answer/Explanation
Answer:
Explaination:
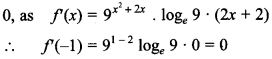
38. Differentiate e-2x with respect to x.
Answer/Explanation
Answer:
Explaination:
![]()
39. Differentiate 5sin x, with respect to x.
Answer/Explanation
Answer:
Explaination:
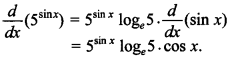
40. Differentiate loge(sin x) with respect to x.
Answer/Explanation
Answer:
Explaination:

41. Differentiate log x² w.r.t x.
Answer/Explanation
Answer:
Explaination:
![]()
42. If y = e-3 log x then find \(\frac{d y}{d x}\).
Answer/Explanation
Answer:
Explaination:

43.

Answer/Explanation
Answer:
Explaination:

44. Find \(\frac{d y}{d x}\) at t = \(\frac{2 \pi}{3}\) when x = 10(t – sin t) and y = 12(1 – cos t). [Foreign 2017]
Answer/Explanation
Answer:
Explaination:

45. Find \(\frac{d^{2} y}{d x^{2}}\), if y = log x
Answer/Explanation
Answer:
Explaination:
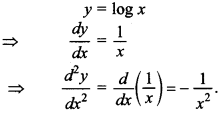
46. If y = sin 3x, find y2
Answer/Explanation
Answer:
Explaination:
y = sin 3x
y1 = 3 cos 3x
y2 = -9 sin 3x.
47. Find \(\frac{d^{2} y}{d x^{2}}\) if y = e-3x
Answer/Explanation
Answer:
Explaination:
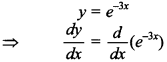

48. Verify the Rolle’s Theorem for the function f(x) = x² in the inverval [-1, 1].
Answer/Explanation
Answer:
Explaination:
Function f(x) = x² is continuous in [-1,1 ], differentiable in ( -1, 1) and f(-1) = f(1). Hence, Rolle’s Theorem verified.
⇒ f'(c) = 0
⇒ 2c = 0
⇒ c = 0 for c ∈ (-1, 1)
49. Verify the Rolle’s Theorem for die functiony(x) = |x| in the inverval [-1, 1]. [HOTS]
Answer/Explanation
Answer:
Explaination: Not verified, as /(x) =|x| is not derivable at x = 0.
50. Verify the Rolle’s Theorem for the function f(x) = sin 2x in [0, π].
Answer/Explanation
Answer:
Explaination:
Function f(x) = sin 2x is continuous in [0, π], differentiable in (0, π) and (0)= f(π)
Hence, Rolle’s theorem verified.
⇒ f'(c) = 2 cos 2c
⇒ 2cos 2c = 0
![]()
We hope the given Maths MCQs for Class 12 with Answers Chapter 5 Continuity and Differentiability will help you. If you have any query regarding CBSE Class 12 Maths Continuity and Differentiability MCQs Pdf, drop a comment below and we will get back to you at the earliest.