ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test
ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test
Question 1.
Write the first four terms of the A.P. when its first term is -5 and the common difference is -3.
Solution:

Question 2.
Verify that each of the following lists of numbers is an A.P., and the write its next three terms:
(i) \(0,\frac { 1 }{ 4 } ,\frac { 1 }{ 2 } ,\frac { 3 }{ 4 } ,… \)
(ii) \(5,\frac { 14 }{ 3 } ,\frac { 13 }{ 3 } ,4,… \)
Solution:

Question 3.
The nth term of an A.P. is 6n + 2. Find the common difference.
Solution:
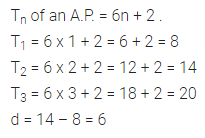
Question 4.
Show that the list of numbers 9, 12, 15, 18, … form an A.P. Find its 16th term and the nth.
Solution:

Question 5.
Find the 6th term from the end of the A.P. 17, 14, 11, …, -40.
Solution:
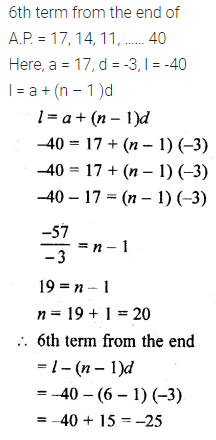
Question 6.
If the 8th term of an A.P. is 31 and the 15th term is 16 more than its 11th term, then find the A.P.
Solution:

Question 7.
The 17th term of anA.P. is 5 more than twice its 8th term. If the 11th term of the A.P. is 43, then find the wth term.
Solution:

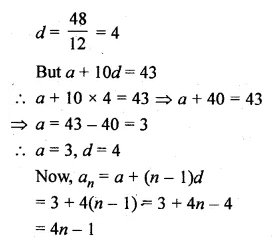
Question 8.
The 19th term of an A.P. is equal to three times its 6th term. If its 9th term is 19, find the A.P.
Solution:
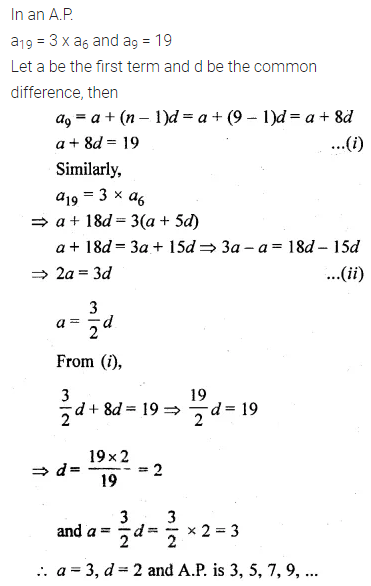
Question 9.
If the 3rd and the 9th terms of an A.P. are 4 and -8 respectively, then which term of this A.P. is zero?
Solution:

Question 10.
Which term of the list of numbers 5, 2, -1, -4, … is -55?
Solution:
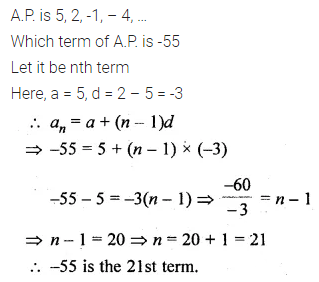
Question 11.
The 24th term of an A.P. is twice its 10th term. Show that its 72nd term is four times its 15th term.
Solution:

Question 12.
Which term of the list of numbers \(20,19\frac { 1 }{ 4 } ,18\frac { 1 }{ 2 } ,17\frac { 3 }{ 4 } ,..\) is the first negative term?
Solution:
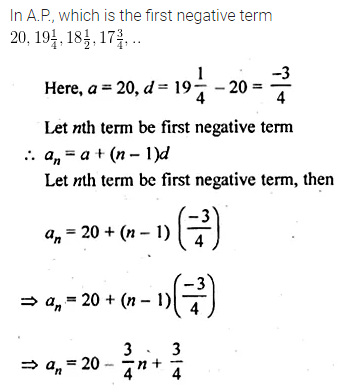
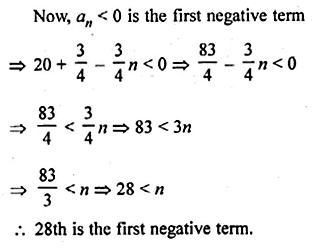
Question 13.
If the pth term of an A.P. is q and the qth term is p, show that its nth term is (p + q – n)
Solution:

Question 14.
How many three-digit numbers are divisible by 9?
Solution:
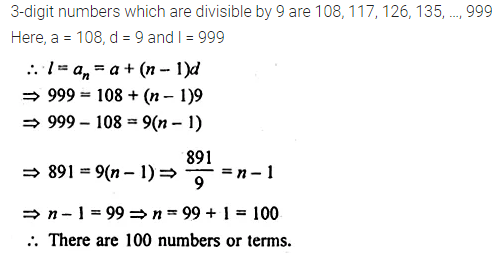
Question 15.
The sum of three numbers in A.P. is -3 and the product is 8. Find the numbers.
Solution:
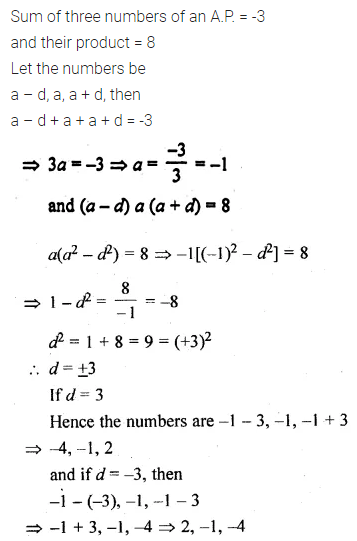
Question 16.
The angles of a quadrilateral are in A.P. If the greatest angle is double of the smallest angle, find all the four angles.
Solution:

Question 17.
The nth term of an A.P. cannot be n² + n + 1. Justify your answer.
Solution:

Question 18.
Find the sum of first 20 terms of an A.P. whose nth term is 15 – 4n.
Solution:
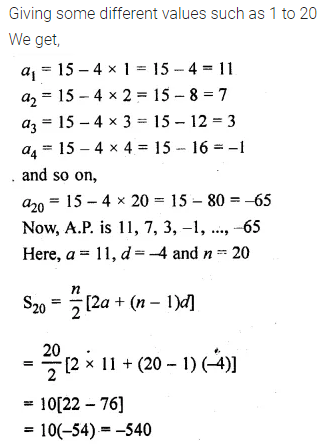
Question 19.
Find the sum :
\(18+15\frac { 1 }{ 2 } +13+…+\left( -49\frac { 1 }{ 2 } \right) \)
Solution:
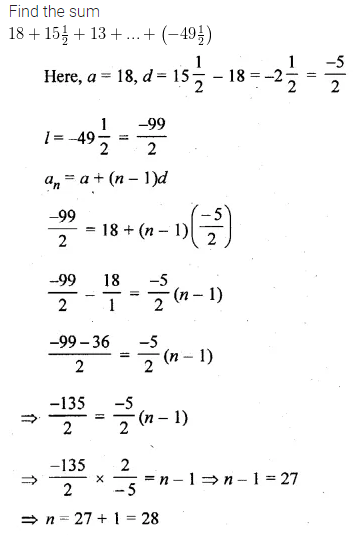
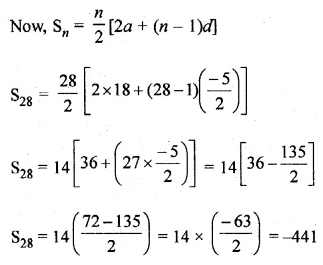
Question 20.
(i) How many terms of the A.P. -6,\(– \frac { 11 }{ 2 } \) -5,… make the sum -25?
(ii) Solve the equation 2 + 5 + 8 + … + x = 155.
Solution:



Question 21.
If the third term of an A.P. is 5 and the ratio of its 6th term to the 10th term is 7 : 13, then find the sum of first 20 terms of this A.P.
Solution:

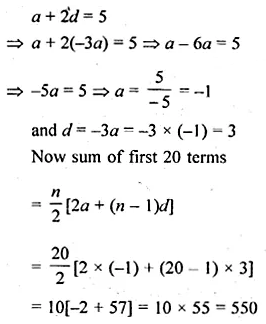
Question 22.
In an A.P., the first term is 2 and the last term is 29. If the sum of the terms is 155, then find the common difference of the A.P.
Solution:
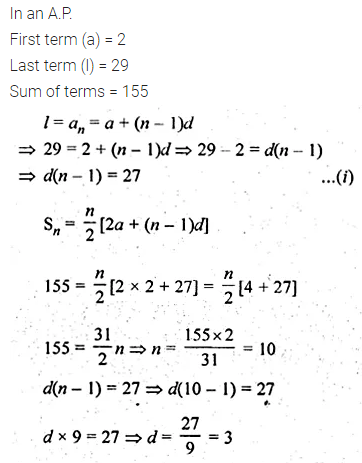
Question 23.
The sum of the first 14 terms of an A.P. is 1505 and its first term is 10. Find its 25th term.
Solution:
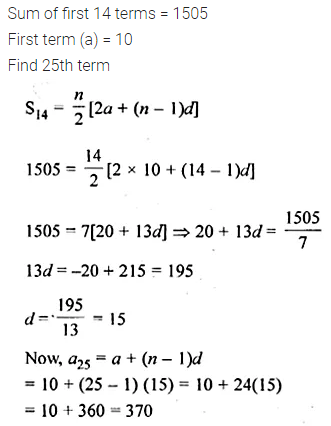
Question 24.
Find the number of terms of the A.P. -12, -9, -6, …, 21. If 1 is added to each term of this A.P., then find the sum of all terms of the A.P. thus obtained.
Solution:
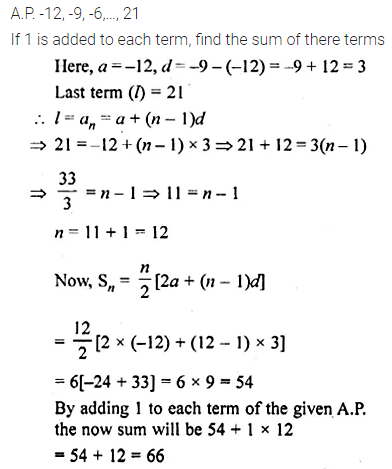
Question 25.
The sum of first n term of an A.P. is 3n² + 4n. Find the 25th term of this A.P.
Solution:
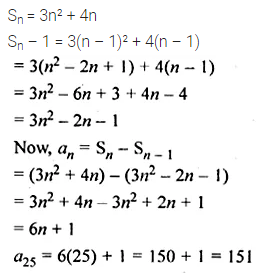
Question 26.
In an A.P., the sum of the first 10 terms is -150 and the sum of the next 10 terms is -550. Find A.P.
Solution:


Question 27.
The sum of first m terms of an A.P. is 4m² – m. If its nth term is 107, find the value of n. Also, find the 21 st term of this A.P.
Solution:
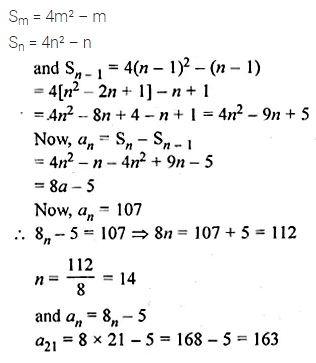
Question 28.
If the sum of first p, q and r terms of an A.P. are a, b and c respectively, prove that
\(\frac { a }{ p } (q-r)+\frac { b }{ q } (r-p)+\frac { c }{ r } (p-q)=0 \)
Solution:

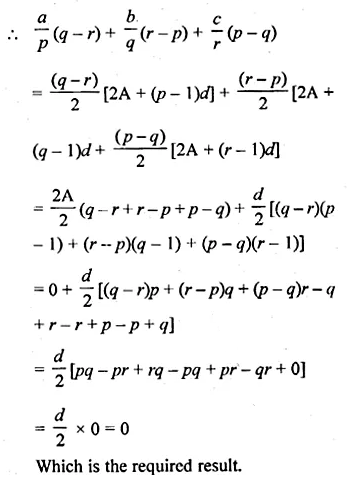
Question 29.
A sum of Rs 700 is to be used to give 7 cash prizes to students of a school for their overall academic performance. If each prize is Rs 20 less than its preceding prize, find the value of each of the prizes.
What is the importance of academic prise in students life? (Value Based)
Solution:

Question 30.
Find the geometric progression whose 4th term is 54 and 7th term is 1458.
Solution:

Question 31.
The fourth term of a G.P. is the square of its second term and the first term is -3. Find its 7th term.
Solution:
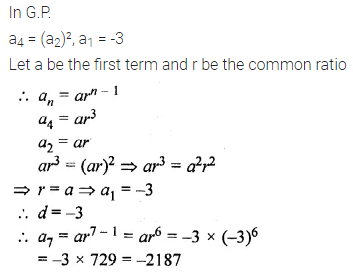
Question 32.
If the 4th, 10th and 16th terms of a G.P. are x, y, and z respectively, prove that x, y, and z are in G.P.
Solution:

Question 33.
The original cost of a machine is Rs 10000. If the annual depreciation is 10%, after how many years will it be valued at Rs 6561?
Solution:


Question 34.
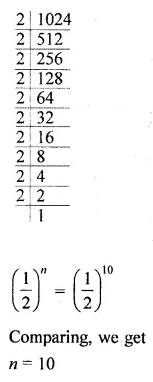
How many terms of the G.P. \(3,\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } \),are needed to give the sum \(\\ \frac { 3069 }{ 512 } \) ?
Solution:
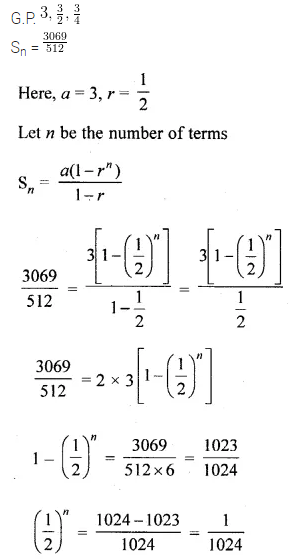
Question 35.
Find the sum of first n terms of the series : 3 + 33 + 333 + …
Solution:

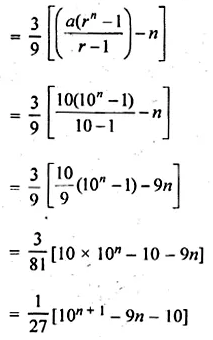
Question 36.
Find the sum of the series 7 + 7.7 + 7.77 + 7.777 + … to 50 terms.
Solution:

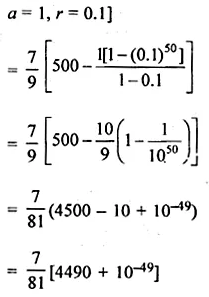
Question 37.
The inventor of the chessboard was a very clever man. He asked the king, h reward of one grain of wheat for the first square, 2 grains for the second, 4 grains for the third, and so on, doubling the number of the grains for each subsequent square. How many grains would have to be given?
Solution:
